-
心电图(electrocardiogram, ECG)诊断心脏疾病的严格标准, 要求有效地消除噪声并准确地重建ECG信号. 经验模式分解(empirical mode decomposition, EMD)方法重建ECG信号中, 模式混叠及重建采用模式分量的识别以经验为基础, 导致重建ECG信号准确度降低, 且方法不具有自适应和通用性. 本文首先基于积分均值定理提出一种改进的EMD方法—积分均值模式分解(integral mean mode decomposition, IMMD)方法, 经5000个高斯白噪声样本的蒙特卡罗法验证, IMMD方法比EMD具有更优多分辨率分析能力, 能够有效地缓解模式混叠. 其次, 基于ECG信号内固有心动物理特征量识别重建ECG信号所采用的模式分量, 具有现实物理意义, 因此, 方法具有自适应和通用性. 经验证, 提出方法重建47例ECG信号与原ECG信号的相关系数中: 31例优于变分模式分解方法; 33例优于Haar小波软阈值法; 42例优于集总经验模式分解方法; 45例优于EMD方法. 相关系数均值为0.8904, 方差为0.0071, 表现稳定且最优.Electrocardiogram (ECG) diagnosis is based on the waveform, duration and amplitude of characteristic wave, which are required to have a high accuracy for ECG signal reconstruction. As an effective nonlinear signal processing method, empirical mode decomposition (EMD) has been widely used for diagnosing and reconstructing the ECG signal, but there are two problems arising here. One is the mode mixing, and the other is that the mode components used in reconstruction are identified by experience. Therefore, the method of reconstruction is not adaptive and universal, and reconstructed ECG signal loses accuracy. Firstly, we propose an improved EMD method, which is called integral mean mode decomposition (IMMD). The analysis of 5000 samples of Gaussian white noise shows that IMMD has better multi-resolution analysis ability than EMD, and it can effectively alleviate mode mixing consequently. Secondly, based on the inherent physical characteristics of ECG signal, cardiac cycle or heart rate (HR), it has practical physical significance to identify the mode components used in ECG signal reconstruction. The cardiac cycle feature acts as the intrinsic mode function (IMF) component through two modes. 1) For the low-order IMF that belongs to the ECG signal, the cardiac cycle feature acts as the amplitude modulation. The envelope of the IMF component has the characteristics of the cardiac cycle, and the frequency corresponding to the maximum amplitude in the spectrum of the envelope is equal to HR. 2) For the high-order IMF that belongs to the ECG signal, the cardiac cycle feature acts as frequency modulation. Those IMF components have the harmonic characteristics of periodic heartbeats, and the maximum amplitude in the spectrum corresponds to an integral multiple of HR (usually 1－3 times). The noise attributed to IMF component cannot show the above two cardiac cycle characteristics. Thus the proposed method is adaptive and universal. The 47 ECG signals with baseline drift and muscle artifact noise are tested. The results show that the proposed method is more effective than the variational mode decomposition (VMD), Haar wavelet with soft threshold, ensemble empirical mode decomposition (EEMD) and EMD. Among the 47 correlation coefficients between reconstructed and original ECG signals, the proposed method has 31 better than VMD, 33 better than Haar wavelet, 42 better than EEMD and 45 better than EMD. The mean of 47 correlation coefficients from the proposed method is 0.8904, and the variance is 0.0071, which shows that the proposed method has good performance and stability.
-
Keywords:
- electrocardiogram /
- reconstruction /
- heart rate /
- integral mean mode decomposition
[1] 黄宛 1998 临床心电图学 (第5版) (北京: 人民卫生出版社) 第22, 428页
Huang W 1998 Clinical Electrocardiography (5th Ed.) (Beijing: People's Medical Publishing House Press) pp22, 428 (in Chinese)
[2] Poungponsri S, Yu X H 2013 Neurocomputing 117 206
Google Scholar
[3] 庞宇, 邓璐, 林金朝, 李章勇, 周前能, 李国权, 黄华伟, 张懿, 吴炜 2014 63 098701
Google Scholar
Pang Y, Deng L, Lin J C, Li Z Y, Zhou Q N, Li G Q, Huang H W, Zhang Y, Wu W 2014 Acta Phys. Sin. 63 098701
Google Scholar
[4] Sharma R R, Pachori R B 2018 Biomed. Signal Process. Control 45 33
Google Scholar
[5] de Oliveira B R, Duarte M A Q, de Abreu C C E, Vieira F J 2018 Res. Biomed. Eng. 34 73
Google Scholar
[6] Zou C, Qin Y, Sun C, Li W, Chen W 2017 Pervasive Mob. Comput. 40 267
Google Scholar
[7] Jung W H, Lee S G 2012 Comput. Meth. Programs Biomed. 108 1121
Google Scholar
[8] Yadav S K, Sinha R, Bora P K 2015 IET Signal Proc. 9 88
Google Scholar
[9] Yu Q, Guan Q, Li P, Liu T B, Si J F, Zhao Y, Liu H X, Wang Y Q 2017 Chin. Phys. B 26 118702
Google Scholar
[10] Satija U, Ramkumar B, Manikandan M S 2018 IEEE J. Biomed. Health 22 722
Google Scholar
[11] Huang N E, Shen Z, Long S R, Wu M C, Shih H H, Zheng Q, Yen N C, Tung C C, Liu H H 1998 Proc. R. Soc. Lond. A 454 903
Google Scholar
[12] Fu M J, Zhuang J J, Hou F Z, Zhan Q B, Shao Y, Ning X B 2010 Chin. Phys. B 19 058701
Google Scholar
[13] Zhu Y H, Yuan J, Stephen Z P, Oliver D K, Cheng Q, Wang X D, Tao C, Liu X J, Xu G, Paul L C 2017 Chin. Phys. B 26 064301
Google Scholar
[14] Wu Z, Huang N E 2009 Adv. Adapt. Data Anal. 1 1
Google Scholar
[15] Dragomiretskiy K, Zosso D 2014 IEEE Trans. Signal Process. 62 531
Google Scholar
[16] 曾彭, 刘红星, 宁新宝, 庄建军, 张兴敢 2015 64 078701
Google Scholar
Zeng P, Liu H X, Ning X B, Zhuang J J, Zhang X G 2015 Acta Phys. Sin. 64 078701
Google Scholar
[17] Nazari M, Sakhaei S M 2018 IEEE J. Biomed. Health 22 1059
Google Scholar
[18] Ibtehaz N, Rahman M S, Rahman M S 2019 Biomed. Signal Process. Control 49 349
Google Scholar
[19] Jarchi D, Casson A J 2017 IEEE Trans. Biomed. Eng. 64 2042
Google Scholar
[20] Lee J, McManus D D, Merchant S, Chon K H 2012 IEEE Trans. Biomed. Eng. 59 1499
Google Scholar
[21] 盖强 2001 博士学位论文 (大连: 大连理工大学)
Gai Q 2001 Ph. D. Dissertation (Dalian: Dalian University of Technology) (in Chinese)
[22] Huang N E, Wu M L C, Long S R, Shen S S P, Qu W, Gloersen P, Fan K L 2003 Proc. R. Soc. Lond. A 459 2317
Google Scholar
[23] Flandrin P, Rilling G, Goncalves P 2004 IEEE Signal Process. Lett. 11 112
Google Scholar
[24] Flandrin P, Goncalves P 2004 Int. J. Wavelets Multiresolution. Inf. Process. 2 477
Google Scholar
[25] Huang N E, Hu K, Yang A C C, Chang H C, Jia D, Liang W K, Yeh J R, Kao C L, Juan C H, Peng C K, Meijer J H, Wang Y H, Long S R, Wu Z 2016 Phil. Trans. R. Soc. A 374 20150206
Google Scholar
[26] Moody G B, Mark R G 2001 IEEE Eng. Med. Biol. Mag. 20 45
Google Scholar
[27] Moody G B, Muldrow W E, Mark R G 1984 Comput Cardiol 11 381
[28] Motin M A, Karmakar C, Palaniswami M 2019 IEEE Signal Process. Lett. 26 592
Google Scholar
[29] Li H Y, Wang C J, Zhao D 2018 IET Signal Proc. 12 844
Google Scholar
-
图 1 IMMD和EMD方法分解高斯白噪声的等效滤波器组特性 (a) IMMD (实线)和EMD (虚线)的IMF分量的平均功率谱; (b) 基于(5)式, IMMD (实线)和EMD (虚线)的IMF分量的平均功率谱坍缩重合
Fig. 1. Equivalent filter banks of IMMD and EMD decomposing Gauss white noises: (a) Averaged power spectra of IMFs from IMMD (solid curves) and EMD (dotted curves); (b) collapse and coincidence of the average power spectrum of IMFs from IMMD (solid curves) and EMD (dotted curves) based on Eq. (5).
图 2 实验采用信号波形 (a) 105 ECG信号; (b) BW信号; (c) MA信号; (d)含噪105 ECG信号
Fig. 2. Waveform of signals used in experiment: (a) No. 105 ECG signal; (b) BW signal; (c) MA signal; (d) the noisy No. 105 ECG signal.
图 3 含噪105 ECG信号的IMF (蓝色曲线)及其包络(红色曲线)
Fig. 3. IMF envelopes (red curves) and IMFs (blue curves) of noisy No. 105 ECG signal.
图 4 含噪105 ECG信号IMFs的功率谱(蓝色曲线), 及IMFs包络的功率谱(红色曲线)
Fig. 4. Power spectra of envelopes of IMFs (red curves) and of IMFs (blue curves) of noisy No. 105 ECG signal.
图 5 原105 ECG信号(蓝色点虚线)与由五种方法重建的105 ECG信号(红色实线) (a) 本文方法; (b) VMD; (c) Haar小波软阈值; (d) EMMD; (e) EMD
Fig. 5. Original No. 105 ECG signal (blue dotted curves) and the No. 105 ECG signals (red solid curves) reconstructed by 5 methods: (a) The proposed method; (b) VMD; (c) Haar wavelet with soft threshold; (d) EEMD; (e) EMD.
图 6 采用五种方法重建47个ECG信号的R值柱状图
Fig. 6. Histogram of R values of 47 ECG signals reconstructed by 5 methods.
图 7 采用五种方法重建47个ECG信号的相关系数R值的统计盒子图
Fig. 7. Five box-plots of R values of 47 ECG signals reconstructed by 5 methods.
表 1 五种方法重建105 ECG信号的特征量值
Table 1. Characteristic values of No. 105 ECG signals reconstructed by 5 methods.
重建方法 R SNR/dB MSE/mV2 本文方法 0.9577 10.7740 0.0076 VMD 0.9572 10.6602 0.0078 Haar 0.9434 9.0070 0.0114 EEMD 0.9204 8.1126 0.0140 EMD 0.7638 3.6982 0.0388 
下载: 导出CSV
表 2 实验采用的部分ECG信号对应心律失常类型
Table 2. Type of arrhythmia corresponding to some ECG signals used in the experiment.
心律失常类别 ECG索引号 房性早搏 100, 232 P波峰值和
起搏心搏102, 104, 107, 217 心房颤动 201, 203, 210, 219, 221 预激综合征 230 左束支传导阻滞 109, 111, 214 右束支传导阻滞 118, 124, 207, 212, 231, 232 室性早搏 119, 200, 203, 207, 208, 210,
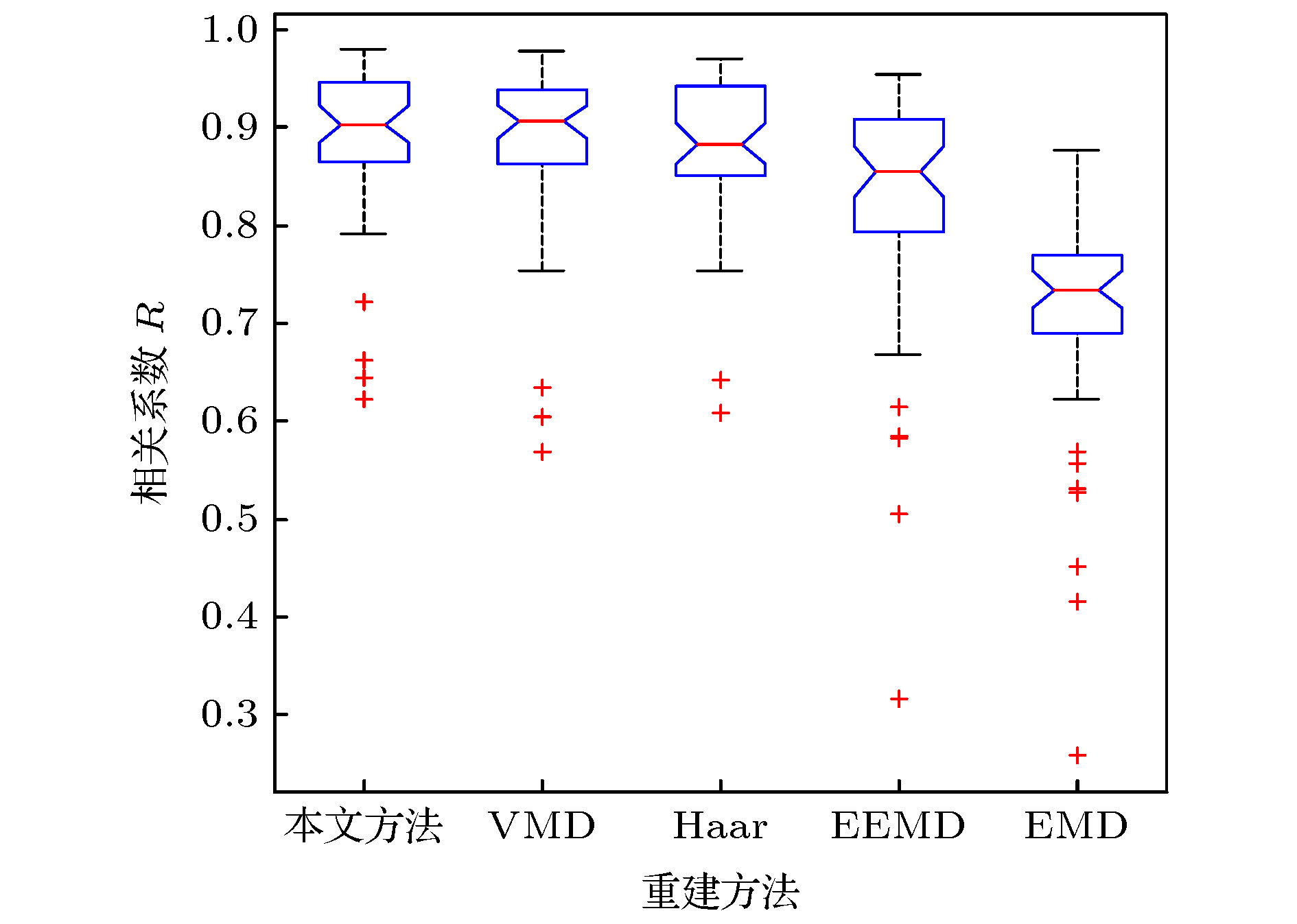
214, 221, 233
下载: 导出CSV
表 3 五种方法重建47个ECG信号的R值的均值与方差
Table 3. Means and variances of R values of 47 ECG signals reconstructed by 5 methods.
重建方法 均值 方差 本文方法 0.8904 0.0071 VMD 0.8826 0.0081 Haar 0.8804 0.0058 EEMD 0.8222 0.0166 EMD 0.7100 0.0143
下载: 导出CSV
-
[1] 黄宛 1998 临床心电图学 (第5版) (北京: 人民卫生出版社) 第22, 428页
Huang W 1998 Clinical Electrocardiography (5th Ed.) (Beijing: People's Medical Publishing House Press) pp22, 428 (in Chinese)
[2] Poungponsri S, Yu X H 2013 Neurocomputing 117 206
Google Scholar
[3] 庞宇, 邓璐, 林金朝, 李章勇, 周前能, 李国权, 黄华伟, 张懿, 吴炜 2014 63 098701
Google Scholar
Pang Y, Deng L, Lin J C, Li Z Y, Zhou Q N, Li G Q, Huang H W, Zhang Y, Wu W 2014 Acta Phys. Sin. 63 098701
Google Scholar
[4] Sharma R R, Pachori R B 2018 Biomed. Signal Process. Control 45 33
Google Scholar
[5] de Oliveira B R, Duarte M A Q, de Abreu C C E, Vieira F J 2018 Res. Biomed. Eng. 34 73
Google Scholar
[6] Zou C, Qin Y, Sun C, Li W, Chen W 2017 Pervasive Mob. Comput. 40 267
Google Scholar
[7] Jung W H, Lee S G 2012 Comput. Meth. Programs Biomed. 108 1121
Google Scholar
[8] Yadav S K, Sinha R, Bora P K 2015 IET Signal Proc. 9 88
Google Scholar
[9] Yu Q, Guan Q, Li P, Liu T B, Si J F, Zhao Y, Liu H X, Wang Y Q 2017 Chin. Phys. B 26 118702
Google Scholar
[10] Satija U, Ramkumar B, Manikandan M S 2018 IEEE J. Biomed. Health 22 722
Google Scholar
[11] Huang N E, Shen Z, Long S R, Wu M C, Shih H H, Zheng Q, Yen N C, Tung C C, Liu H H 1998 Proc. R. Soc. Lond. A 454 903
Google Scholar
[12] Fu M J, Zhuang J J, Hou F Z, Zhan Q B, Shao Y, Ning X B 2010 Chin. Phys. B 19 058701
Google Scholar
[13] Zhu Y H, Yuan J, Stephen Z P, Oliver D K, Cheng Q, Wang X D, Tao C, Liu X J, Xu G, Paul L C 2017 Chin. Phys. B 26 064301
Google Scholar
[14] Wu Z, Huang N E 2009 Adv. Adapt. Data Anal. 1 1
Google Scholar
[15] Dragomiretskiy K, Zosso D 2014 IEEE Trans. Signal Process. 62 531
Google Scholar
[16] 曾彭, 刘红星, 宁新宝, 庄建军, 张兴敢 2015 64 078701
Google Scholar
Zeng P, Liu H X, Ning X B, Zhuang J J, Zhang X G 2015 Acta Phys. Sin. 64 078701
Google Scholar
[17] Nazari M, Sakhaei S M 2018 IEEE J. Biomed. Health 22 1059
Google Scholar
[18] Ibtehaz N, Rahman M S, Rahman M S 2019 Biomed. Signal Process. Control 49 349
Google Scholar
[19] Jarchi D, Casson A J 2017 IEEE Trans. Biomed. Eng. 64 2042
Google Scholar
[20] Lee J, McManus D D, Merchant S, Chon K H 2012 IEEE Trans. Biomed. Eng. 59 1499
Google Scholar
[21] 盖强 2001 博士学位论文 (大连: 大连理工大学)
Gai Q 2001 Ph. D. Dissertation (Dalian: Dalian University of Technology) (in Chinese)
[22] Huang N E, Wu M L C, Long S R, Shen S S P, Qu W, Gloersen P, Fan K L 2003 Proc. R. Soc. Lond. A 459 2317
Google Scholar
[23] Flandrin P, Rilling G, Goncalves P 2004 IEEE Signal Process. Lett. 11 112
Google Scholar
[24] Flandrin P, Goncalves P 2004 Int. J. Wavelets Multiresolution. Inf. Process. 2 477
Google Scholar
[25] Huang N E, Hu K, Yang A C C, Chang H C, Jia D, Liang W K, Yeh J R, Kao C L, Juan C H, Peng C K, Meijer J H, Wang Y H, Long S R, Wu Z 2016 Phil. Trans. R. Soc. A 374 20150206
Google Scholar
[26] Moody G B, Mark R G 2001 IEEE Eng. Med. Biol. Mag. 20 45
Google Scholar
[27] Moody G B, Muldrow W E, Mark R G 1984 Comput Cardiol 11 381
[28] Motin M A, Karmakar C, Palaniswami M 2019 IEEE Signal Process. Lett. 26 592
Google Scholar
[29] Li H Y, Wang C J, Zhao D 2018 IET Signal Proc. 12 844
Google Scholar
下载:
计量
- 文章访问数: 6812
- PDF下载量: 105
- 被引次数: 0
