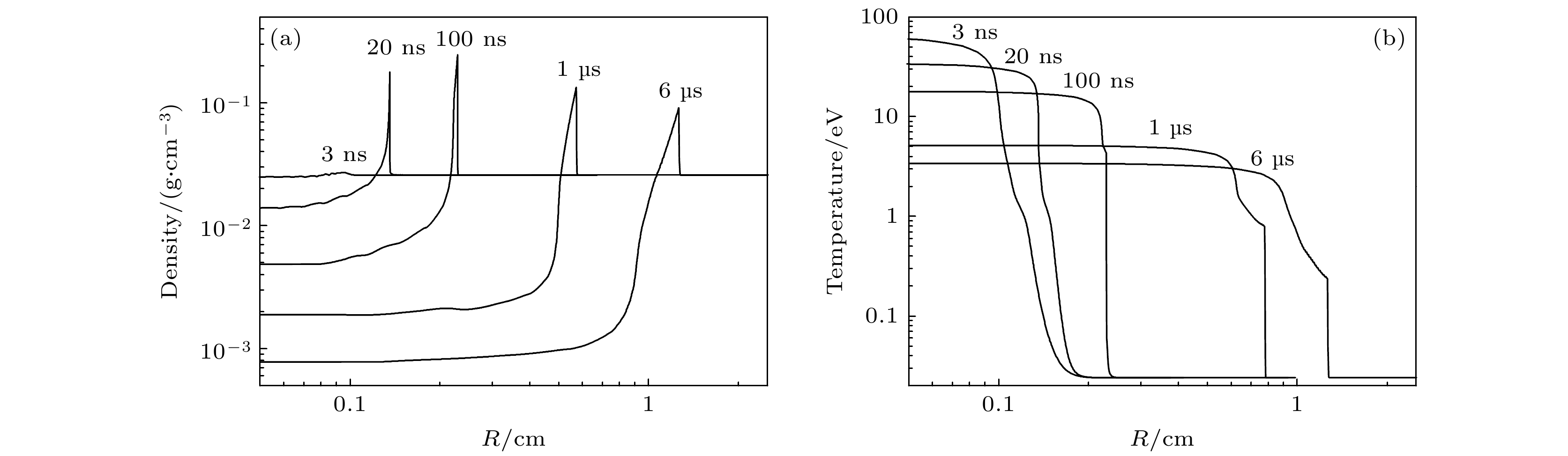
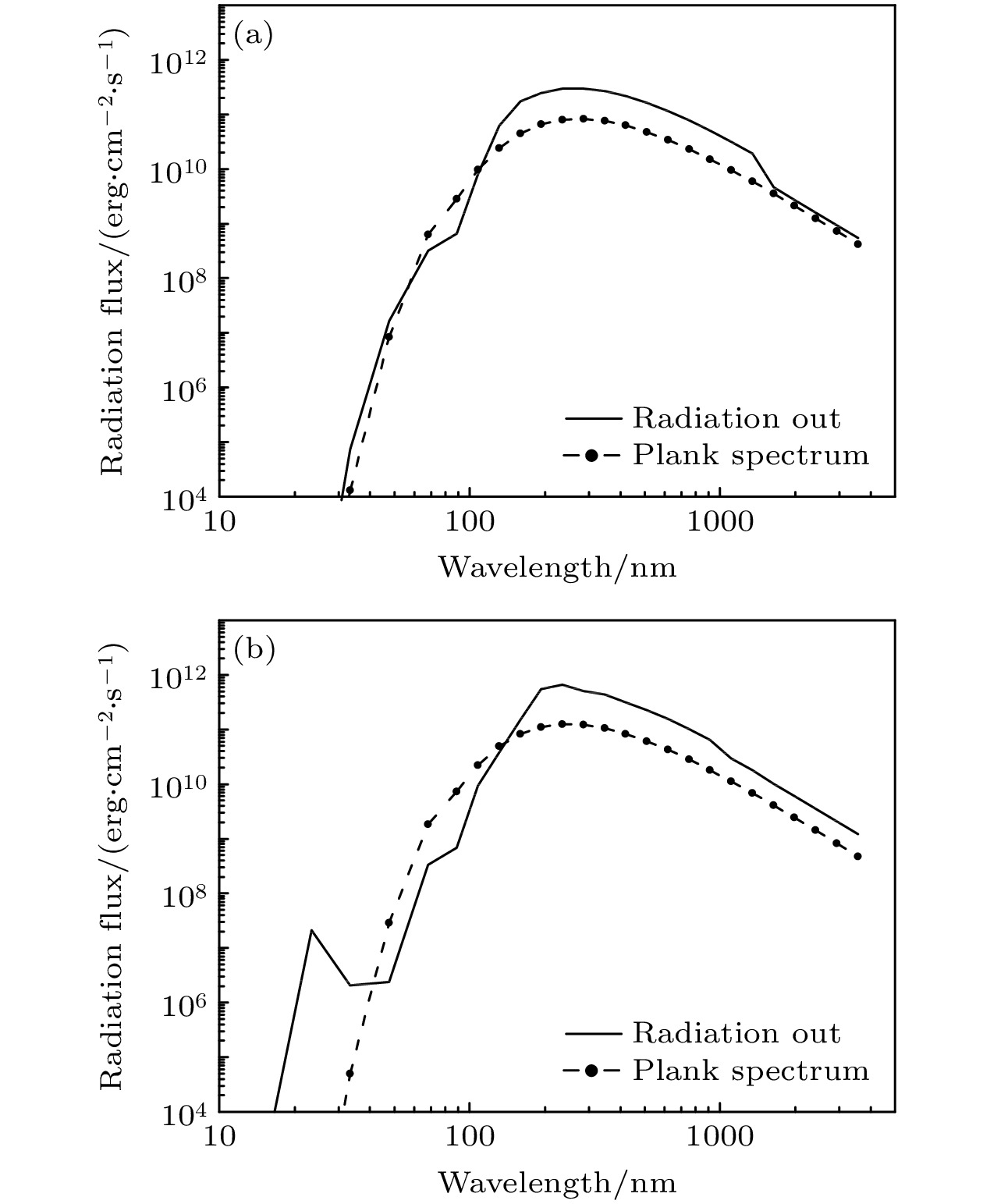
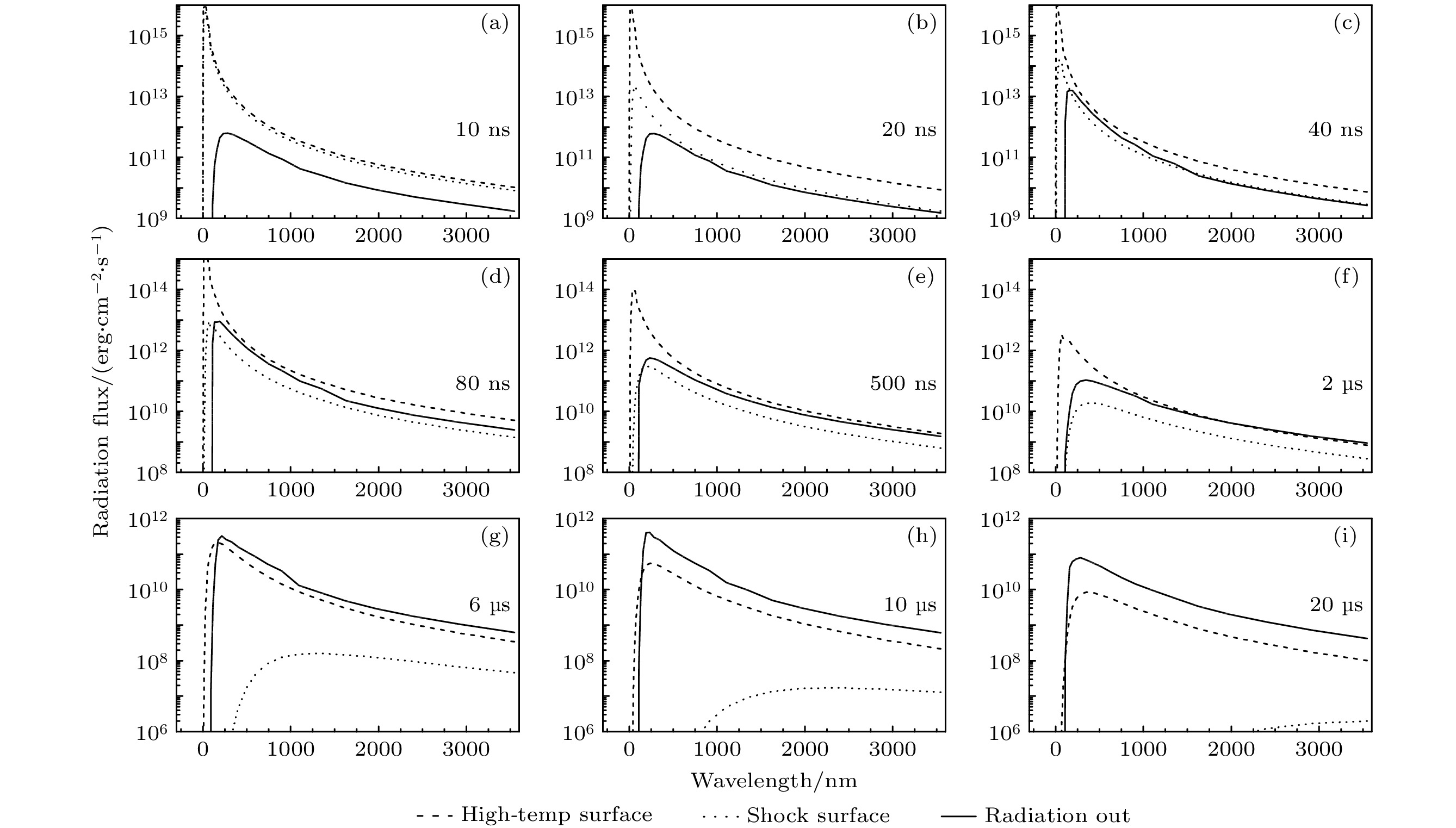
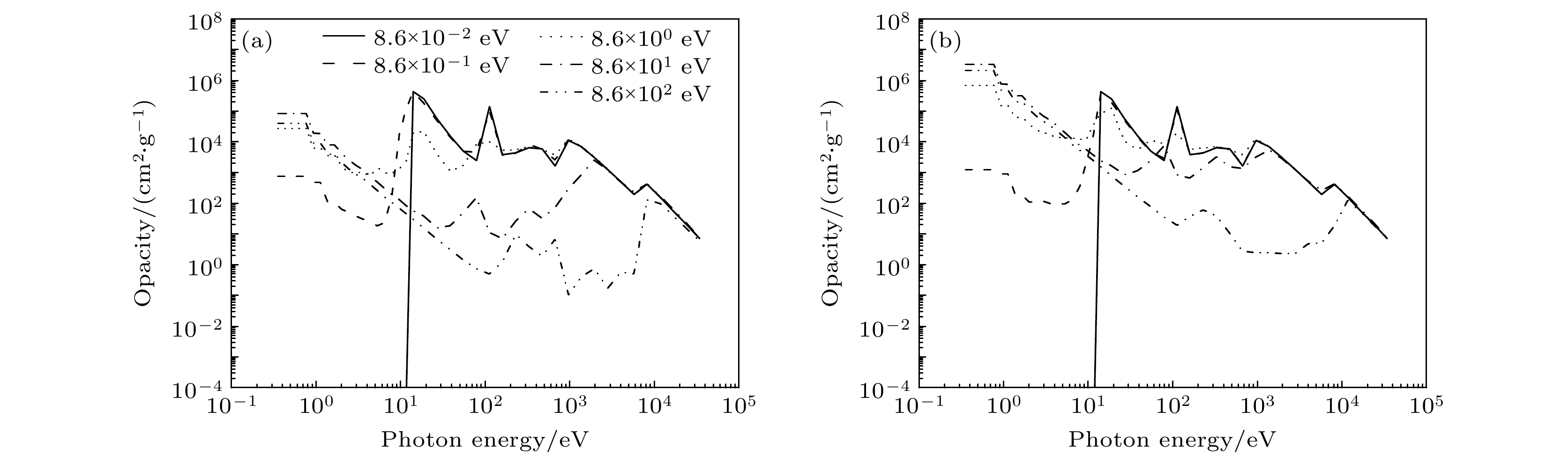
-
Radiative shock is an important phenomenon both in astrophysics and in inertial confinement fusion. In this paper, the radiation properties of X-ray heated radiatve shock in xenon is studied with the simulation method. The radiative shock is described by a one-dimensional, multi-group radiation hydrodynamics model proposed by Zinn [Zinn J 1973 J. Comput. Phys. 13 569]. To conduct computation, the opacity and equation-of-state data of xenon are calculated and put into the model. The reliabilities of the model and the physical parameters of xenon are verified by comparing the temperature and velocity of the radiative shock calculated by the model with those measured experimentally. The evolution of the radiative shock involves abundant physical processes. The core of the xenon can be heated up to 100 eV, resulting in a thermal wave and forming an expanding high-temperature-core. Shortly, the hydrodynamic disturbances reach the thermal wave front, generating a shock. As the thermal wave slows down, the shock gradually exceeds the high-temperature-core, forming a double-step distribution in the temperature profile. The time evolution of the effective temperature of the radiative shock shows two maximum values and one minimum value, and the radiation spectra often deviate from blackbody spectrum. By analyzing the radiation and absorption properties at different positions of the shock, it can be found that the optical property of the shock is highly dynamic and can generate the above-mentioned radiation characteristics. When the radiative shock is just formed, the radiation comes from the shock surface and the shock precursor has a significant absorption of the radiation. As the shock temperature falls during expansion, the shock precursor disappears and the radiation inside the shock can come out owing to absorption coefficient decreases. When the shock becomes transparent, the radiation surface reaches the outside edge of the high-temperature-core. Then, the temperature of the high-temperature-core decreases further, making this region also optically thin, and the radiation from the inner region can come out. Finally, the radiation strength falls because of temperature decreasing. -
Keywords:
- radiative shock /
- radiation spectrum /
- xenon /
- radiation hydrodynamics
[1] Ensman L, Burrows A 1992 Astrophys. J. 393 742
Google Scholar
[2] DE Young D S 1991 Science 252 389
Google Scholar
[3] Chakrabarti S K, Titarchuk L G 1995 Astrophys. J. 455 623
Google Scholar
[4] Pak A, Divol L, Gregori G, Weber S, Atherton J, Bennedetti R, Bradley D K, Callahan D, Casey D T, Dewald E, Döppner T, Edwards M J, Frenje J A, Glenn S, Grim G P, Hicks D, Hsing W W, Izumi N, Jones O S, Johnson M G, Khan S F, Kilkenny J D, Kline J L, Kyrala G A, Lindl J, Landen O L, Le Pape S, Ma T, MacPhee A, MacGowan B J, MacKinnon A J, Masse L, Meezan N B, Moody J D, Olson R E, Ralph J E, Robey H F, Park H S, Remington B A, Ross J S, Tommasini R, Town R P J, Smalyuk V, Glenzer S H, Moses E I 2013 Phys. Plasmas 20 056315
Google Scholar
[5] 江少恩, 李文洪, 孙可煦, 蒋小华, 刘永刚, 崔延莉, 陈久森, 丁永坤, 郑志坚 2004 53 3424
Jiang S E, Li W H, Sun K X, Jiang X H, Liu Y G, Gui Y L, Chen J S, Ding Y K, Zheng Z J 2004 Acta Phys. Sin. 53 3424
[6] Kuranz C C, Park H S, Remington B A, Drake R P, Miles A R, Robey H F, Kilkenny J D, Keane C J, Kalantar D H, Huntington C M, Krauland C M, Harding E C, Grosskopf M J, Marion D C, Doss F W, Myra E, Maddox B, Young B, Kline J L, Kyrala G, Plewa T, Wheeler J C, Arnett W D, Wallace R J, Giraldez E, Nikroo A 2011 Astrophys. Space Sci. 336 207
Google Scholar
[7] Tubman E R, Scott R H H, Doyle H W, Meinecke J, Ahmed H, Alraddadi R A B, Bolis R, Cross J E, Crowston R, Doria D, Lamb D, Reville B, Robinson A P L, Tzeferacos P, Borghesi M, Gregori G, Woolsey N C 2017 Phys. Plasmas 24 103124
Google Scholar
[8] Remington B A, Drake R P, Ryutov D D 2006 Rev. Mod. Phys. 78 755
Google Scholar
[9] Edens A D, Ditmire T, Hansen J F, Edwards M J, Adams R G, Rambo P, Ruggles L, Smith I C, Porter J L 2004 Phys. Plasmas 11 4968
Google Scholar
[10] Reighard A B, Drake R P, Dannenberg K K, Kremer D J, Grosskopf M, Harding E C, Leibrandt D R, Glendinning S G, Perry T S, Remington B A, Greenough J, Knauer J, Boehly T, Bouquet S, Boireau L, Koenig M, Vinci T 2006 Phys. Plasmas 13 082901
Google Scholar
[11] Benuzzi A, Koenig M, Faral B, Krishnan J, Pisani F, Batani D, Bossi S, Beretta D, Hall T, Ellwi S, Hüller S, Honrubia J, Grandjouan N 1998 Phys. Plasmas 5 2410
Google Scholar
[12] Hansen J F, Edwards M J, Froula D H, Edens A D, Gregori G, Ditmire T 2007 Astrophys. Space Sci. 307 219
Google Scholar
[13] Bouquet S, Stéhlé C, Koenig M, Chiéze J P, Benuzzi-Mounaix A, Batani D, Leygnac S, Fleury X, Merdji H, Michaut C, Thais F, Grandjouan N, Hall T, Henry E, Malka V, Lafon J P J 2004 Phys. Rev. Lett. 92 225001
Google Scholar
[14] Morioka T, Sakurai N, Maeno K, Honma H 2000 J. Visulaization. 3 51
Google Scholar
[15] Bykovaa N G, Zabelinskiia I E, Ibragimovaa L B, Kozlova P V, Stovbunb S V, Terezab A M, Shatalova O P 2018 Russ. J. Phys. Chem. B 12 108
Google Scholar
[16] Hall T A, Benuzzi A, Batani D, Beretta D, Bossi S, Faral B, Koenig M, Krishnan J, Löwer T, Mahdieh M 1997 Phys. Rev. E 55 6
[17] Vinci T, Koenig M, Benuzzi-Mounaix A, Michaut C, Boireau L, Leygnac S, Bouquet S, Peyrusse O, Batani D 2006 Phys. Plasmas 13 010702
Google Scholar
[18] Koenig M, Vinci T, Benuzzi-Mounaix A, Ozaki N, Ravasio A, Rabec le Glohaec M, Boireau L, Michaut C, Bouquet S, Atzeni S, Schiavi A, Peyrusse O, Batani D 2006 Phys. Plasmas 13 056504
Google Scholar
[19] Kuramitsu Y, Ohnishi N, Sakawa Y, Morita T, Tanji H, Ide T, Nishio K, Gregory C D, Waugh J N, Booth N, Heathcote R, Murphy C, Gregori G, Smallcombe J, Barton C, Dizière A, Koenig M, Woolsey N, Matsumoto Y, Mizuta A, Sugiyama T, Matsukiyo S, Moritaka T, Sano T, Takabe H 2016 Phys. Plasmas 23 032126
Google Scholar
[20] Benuzzi-Mounaix A, Koenig M, Ravasio A, Vinci T, Ozaki N, Rabec le Gloahec M, Loupias B, Huser G, Henry E, Bouquet S, Michaut C, Hicks D, MacKinnon A, Patel P, Park H S, Le Pape S, Boehly T, Borghesi M, Cecchetti C, Notley M, Clark R, Bandyopadhyay S, Atzeni S, Schiavi A, Aglitskiy Y, Faenov A, Pikuz T, Batani D, Dezulian R, Tanaka K 2006 Plasma Phys. Controlled Fusion 48 B347
Google Scholar
[21] Zheng J, Gu Y J, Chen Z Y, Chen Q F 2010 Phys. Rev. E 82 026401
Google Scholar
[22] 王瑞荣, 王伟, 方智恒, 安红海, 贾果, 谢志勇, 孟祥富 2013 62 125202
Wang R R, Wang W, Fang Z H, An H H, Jia G, Xie Z Y, Meng X F 2013 Acta Phys. Sin. 62 125202
[23] Sen H K, Guess A W 1957 Phys. Rev. 108 560
Google Scholar
[24] 泽尔道维奇, 莱伊捷尔 著 (张树材 译) 2016 激波和高温流体动力学现象物理学 (北京: 科学出版社)
Zel’dovich Y B, Raizer, Y P (translated by Zhang S C) 2016 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena (Beijing: Science Press) (in Chinese)
[25] Drake R P 2007 Phys. Plasmas 14 043301
Google Scholar
[26] McClarren R G, Drake R P, Morel J E, Holloway J P 2010 Phys. Plasmas 17 093301
Google Scholar
[27] Mabey P, Michel T, Albertazzi B, Falize E, Koenig M 2020 Phys. Plasmas 27 083302
Google Scholar
[28] Zinn J 1973 J. Comput. Phys. 13 569
Google Scholar
[29] Yan J, Wu Z Q 2002 Phys. Rev. E 65 066401
Google Scholar
[30] Bauche-Arnoult C, Bauche J, Klapisch M 1979 Phys. Rev. A 20 2424
Google Scholar
[31] Bar-Shalom A, Oreg J, Goldstein W H 1995 Phys. Rev. E 51 4882
[32] Jin F, Zeng J, Yuan J, Han G X, Wu Z Q, Yan J, Wang M S, Peng Y L 2005 JQSRT 95 241
Google Scholar
[33] Li Q, Liu H F, Zhang G M, Zhao Y H, Lu G, Tian M F, Song H F 2016 Phys. Plasmas 23 112709
Google Scholar
[34] 尼基弗洛夫, 诺维科夫, 乌瓦洛夫 著 (李国政 译) 2004 高温等离子体辐射不透明度和状态方程的计算 (北京: 国防工业出版社)
Никифоров А Ф, Новиков В Г, Уваров В Б (Переводчик Li G Z) 2004 Квантово-Статистические Модели Высокотемпературной Плазмы И Методы Расчета Росселандовых Пробегов И Уравнений Состояния (Пекин: Издательство Оборонной Промышленности) Глава IV и глава VI, раздел III (Перевод На Китайский Язык)
[35] Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2020 https://physics.nist.gov/asd
[36] Schmalz R F, Meyer-ter-Vehn J, Ramis R 1986 Phys. Rev. A 34 2177
Google Scholar
-
图 1 不同气体密度时氙气的辐射不透明度随光子能量的变化 (a) ρ = 5.33 × 10–7 g/cm3; (b) ρ = 5.33 × 10–3 g/cm3. 不同曲线类型表示不同的温度 (1 eV = 11610 K)
Fig. 1. Opacity data of xenon at the density of 5.33 × 10–7 g/cm3 (a) and 5.33 × 10–3 g/cm3 (b), lines with different style represent different temperature.
图 2 氙气的状态方程数据 (a)温度(T, 单位为eV)与比内能(E, 单位为erg/g (1 erg/g = 10–7 J/g))之比随E的变化; (b)压强(P, 单位dyn/cm2 (1 dyn/ cm2 = 10–5 N/ cm2))与E和密度(
$ \rho $ , 单位g/cm3)乘积之比随E的变化. 参数使用比值形式是为方便程序计算Fig. 2. Equation-of-state data of xenon: (a) Variation of the ratio between temperature (T, in eV) and specific inertial energy (E, in erg/g) with E; (b) variation of ratio between pressure (P, in dyn/cm2) and the multiplication of E and density (
$ \rho $ , in g/cm3) with E. The parameters are shown by ratios for computation convenience.
图 3 不同时刻氙气中的密度(a)和温度(b)的位置分布
Fig. 3. Variation of density (a) and temperature (b) with position at different times in xenon.
图 4 氙气中辐射激波等效温度(
$ {T}_{\rm{eff}} $ , eV)的时间演化曲线Fig. 4. Time evolution of the effective temperature (
$ {T}_{\rm{eff}} $ , in eV) of radiative shock in xenon.
图 5 辐射激波不同波段辐射能流的时间演化, 图像亮度代表辐射能流大小
Fig. 5. Time evolution of radiation flux at different wavelength of the radiative shock, and the radiation flux are represented by the brightness of the figure.
图 6 不同时刻氙气的对外辐射光谱与相同等效温度下的黑体辐射光谱的比较 (a) 1 μs; (b) 6 μs
Fig. 6. Spectrums radiated from radiative shock in xenon and spectrums of blackbody radiation at the same effective temperature at different time: (a) 1 μs; (b) 6 μs.
图 7 高温区表面(虚线)、激波表面(点线)的黑体辐射光谱与氙气对外辐射光谱(实线)的比较. (a)−(i)代表不同时刻的计算结果, 辐射能流统一投影到激波表面以避免球几何发散带来的影响
Fig. 7. Comparison among the blackbody spectrums at the surface of high-temperature-core (dash line), at the surface of the shock (dotted line), and the radiation spectrum outward-emitted by the radiative shock (solid line). (a)−(i) represent the result at different time, and all the radiation fluxes are projected on the shock surfaces to eliminate the spherical spreading effect.
-
[1] Ensman L, Burrows A 1992 Astrophys. J. 393 742
Google Scholar
[2] DE Young D S 1991 Science 252 389
Google Scholar
[3] Chakrabarti S K, Titarchuk L G 1995 Astrophys. J. 455 623
Google Scholar
[4] Pak A, Divol L, Gregori G, Weber S, Atherton J, Bennedetti R, Bradley D K, Callahan D, Casey D T, Dewald E, Döppner T, Edwards M J, Frenje J A, Glenn S, Grim G P, Hicks D, Hsing W W, Izumi N, Jones O S, Johnson M G, Khan S F, Kilkenny J D, Kline J L, Kyrala G A, Lindl J, Landen O L, Le Pape S, Ma T, MacPhee A, MacGowan B J, MacKinnon A J, Masse L, Meezan N B, Moody J D, Olson R E, Ralph J E, Robey H F, Park H S, Remington B A, Ross J S, Tommasini R, Town R P J, Smalyuk V, Glenzer S H, Moses E I 2013 Phys. Plasmas 20 056315
Google Scholar
[5] 江少恩, 李文洪, 孙可煦, 蒋小华, 刘永刚, 崔延莉, 陈久森, 丁永坤, 郑志坚 2004 53 3424
Jiang S E, Li W H, Sun K X, Jiang X H, Liu Y G, Gui Y L, Chen J S, Ding Y K, Zheng Z J 2004 Acta Phys. Sin. 53 3424
[6] Kuranz C C, Park H S, Remington B A, Drake R P, Miles A R, Robey H F, Kilkenny J D, Keane C J, Kalantar D H, Huntington C M, Krauland C M, Harding E C, Grosskopf M J, Marion D C, Doss F W, Myra E, Maddox B, Young B, Kline J L, Kyrala G, Plewa T, Wheeler J C, Arnett W D, Wallace R J, Giraldez E, Nikroo A 2011 Astrophys. Space Sci. 336 207
Google Scholar
[7] Tubman E R, Scott R H H, Doyle H W, Meinecke J, Ahmed H, Alraddadi R A B, Bolis R, Cross J E, Crowston R, Doria D, Lamb D, Reville B, Robinson A P L, Tzeferacos P, Borghesi M, Gregori G, Woolsey N C 2017 Phys. Plasmas 24 103124
Google Scholar
[8] Remington B A, Drake R P, Ryutov D D 2006 Rev. Mod. Phys. 78 755
Google Scholar
[9] Edens A D, Ditmire T, Hansen J F, Edwards M J, Adams R G, Rambo P, Ruggles L, Smith I C, Porter J L 2004 Phys. Plasmas 11 4968
Google Scholar
[10] Reighard A B, Drake R P, Dannenberg K K, Kremer D J, Grosskopf M, Harding E C, Leibrandt D R, Glendinning S G, Perry T S, Remington B A, Greenough J, Knauer J, Boehly T, Bouquet S, Boireau L, Koenig M, Vinci T 2006 Phys. Plasmas 13 082901
Google Scholar
[11] Benuzzi A, Koenig M, Faral B, Krishnan J, Pisani F, Batani D, Bossi S, Beretta D, Hall T, Ellwi S, Hüller S, Honrubia J, Grandjouan N 1998 Phys. Plasmas 5 2410
Google Scholar
[12] Hansen J F, Edwards M J, Froula D H, Edens A D, Gregori G, Ditmire T 2007 Astrophys. Space Sci. 307 219
Google Scholar
[13] Bouquet S, Stéhlé C, Koenig M, Chiéze J P, Benuzzi-Mounaix A, Batani D, Leygnac S, Fleury X, Merdji H, Michaut C, Thais F, Grandjouan N, Hall T, Henry E, Malka V, Lafon J P J 2004 Phys. Rev. Lett. 92 225001
Google Scholar
[14] Morioka T, Sakurai N, Maeno K, Honma H 2000 J. Visulaization. 3 51
Google Scholar
[15] Bykovaa N G, Zabelinskiia I E, Ibragimovaa L B, Kozlova P V, Stovbunb S V, Terezab A M, Shatalova O P 2018 Russ. J. Phys. Chem. B 12 108
Google Scholar
[16] Hall T A, Benuzzi A, Batani D, Beretta D, Bossi S, Faral B, Koenig M, Krishnan J, Löwer T, Mahdieh M 1997 Phys. Rev. E 55 6
[17] Vinci T, Koenig M, Benuzzi-Mounaix A, Michaut C, Boireau L, Leygnac S, Bouquet S, Peyrusse O, Batani D 2006 Phys. Plasmas 13 010702
Google Scholar
[18] Koenig M, Vinci T, Benuzzi-Mounaix A, Ozaki N, Ravasio A, Rabec le Glohaec M, Boireau L, Michaut C, Bouquet S, Atzeni S, Schiavi A, Peyrusse O, Batani D 2006 Phys. Plasmas 13 056504
Google Scholar
[19] Kuramitsu Y, Ohnishi N, Sakawa Y, Morita T, Tanji H, Ide T, Nishio K, Gregory C D, Waugh J N, Booth N, Heathcote R, Murphy C, Gregori G, Smallcombe J, Barton C, Dizière A, Koenig M, Woolsey N, Matsumoto Y, Mizuta A, Sugiyama T, Matsukiyo S, Moritaka T, Sano T, Takabe H 2016 Phys. Plasmas 23 032126
Google Scholar
[20] Benuzzi-Mounaix A, Koenig M, Ravasio A, Vinci T, Ozaki N, Rabec le Gloahec M, Loupias B, Huser G, Henry E, Bouquet S, Michaut C, Hicks D, MacKinnon A, Patel P, Park H S, Le Pape S, Boehly T, Borghesi M, Cecchetti C, Notley M, Clark R, Bandyopadhyay S, Atzeni S, Schiavi A, Aglitskiy Y, Faenov A, Pikuz T, Batani D, Dezulian R, Tanaka K 2006 Plasma Phys. Controlled Fusion 48 B347
Google Scholar
[21] Zheng J, Gu Y J, Chen Z Y, Chen Q F 2010 Phys. Rev. E 82 026401
Google Scholar
[22] 王瑞荣, 王伟, 方智恒, 安红海, 贾果, 谢志勇, 孟祥富 2013 62 125202
Wang R R, Wang W, Fang Z H, An H H, Jia G, Xie Z Y, Meng X F 2013 Acta Phys. Sin. 62 125202
[23] Sen H K, Guess A W 1957 Phys. Rev. 108 560
Google Scholar
[24] 泽尔道维奇, 莱伊捷尔 著 (张树材 译) 2016 激波和高温流体动力学现象物理学 (北京: 科学出版社)
Zel’dovich Y B, Raizer, Y P (translated by Zhang S C) 2016 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena (Beijing: Science Press) (in Chinese)
[25] Drake R P 2007 Phys. Plasmas 14 043301
Google Scholar
[26] McClarren R G, Drake R P, Morel J E, Holloway J P 2010 Phys. Plasmas 17 093301
Google Scholar
[27] Mabey P, Michel T, Albertazzi B, Falize E, Koenig M 2020 Phys. Plasmas 27 083302
Google Scholar
[28] Zinn J 1973 J. Comput. Phys. 13 569
Google Scholar
[29] Yan J, Wu Z Q 2002 Phys. Rev. E 65 066401
Google Scholar
[30] Bauche-Arnoult C, Bauche J, Klapisch M 1979 Phys. Rev. A 20 2424
Google Scholar
[31] Bar-Shalom A, Oreg J, Goldstein W H 1995 Phys. Rev. E 51 4882
[32] Jin F, Zeng J, Yuan J, Han G X, Wu Z Q, Yan J, Wang M S, Peng Y L 2005 JQSRT 95 241
Google Scholar
[33] Li Q, Liu H F, Zhang G M, Zhao Y H, Lu G, Tian M F, Song H F 2016 Phys. Plasmas 23 112709
Google Scholar
[34] 尼基弗洛夫, 诺维科夫, 乌瓦洛夫 著 (李国政 译) 2004 高温等离子体辐射不透明度和状态方程的计算 (北京: 国防工业出版社)
Никифоров А Ф, Новиков В Г, Уваров В Б (Переводчик Li G Z) 2004 Квантово-Статистические Модели Высокотемпературной Плазмы И Методы Расчета Росселандовых Пробегов И Уравнений Состояния (Пекин: Издательство Оборонной Промышленности) Глава IV и глава VI, раздел III (Перевод На Китайский Язык)
[35] Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2020 https://physics.nist.gov/asd
[36] Schmalz R F, Meyer-ter-Vehn J, Ramis R 1986 Phys. Rev. A 34 2177
Google Scholar
下载:
计量
- 文章访问数: 5145
- PDF下载量: 99
- 被引次数: 0
