-
基于密度泛函理论结合粒子群优化算法程序CALYPSO研究了掺Be硼团簇BeB
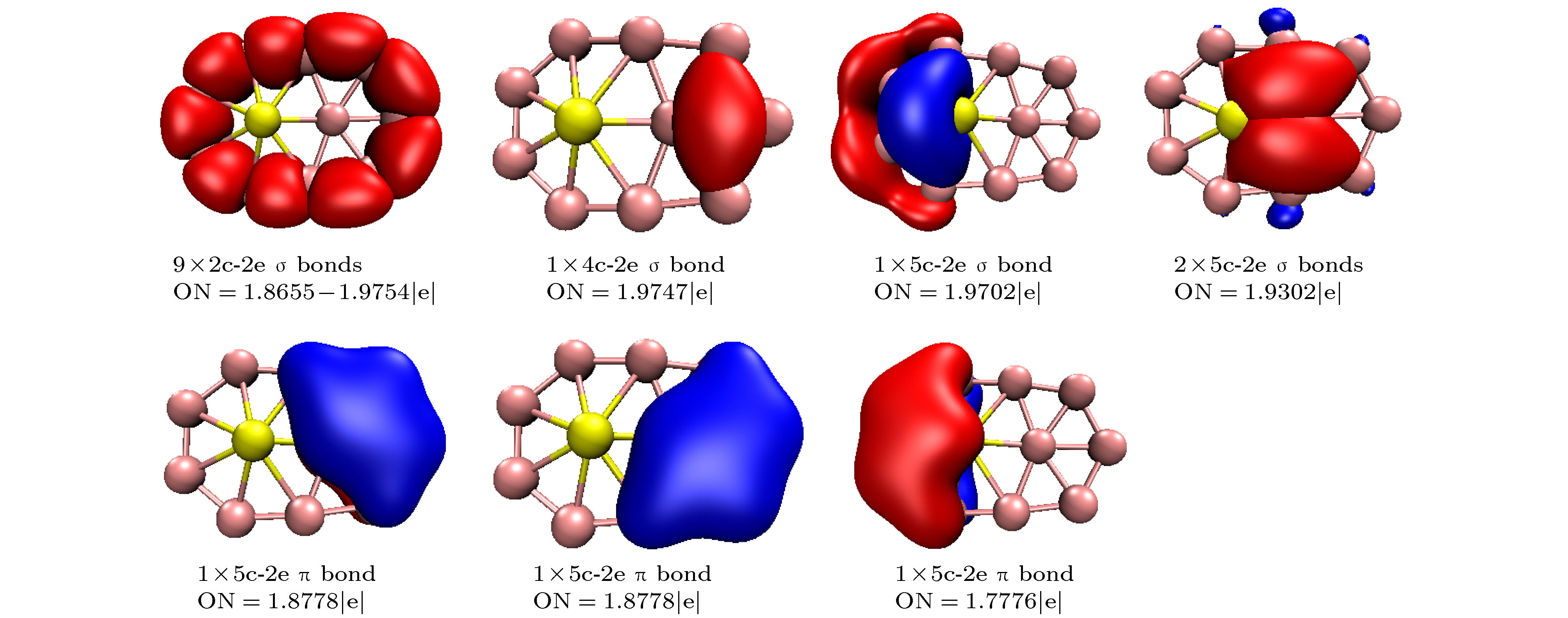
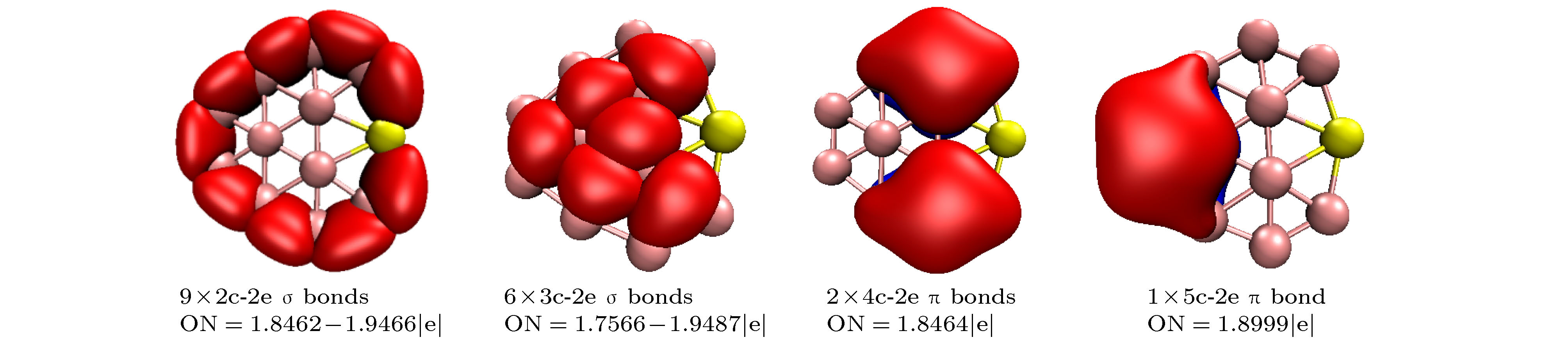
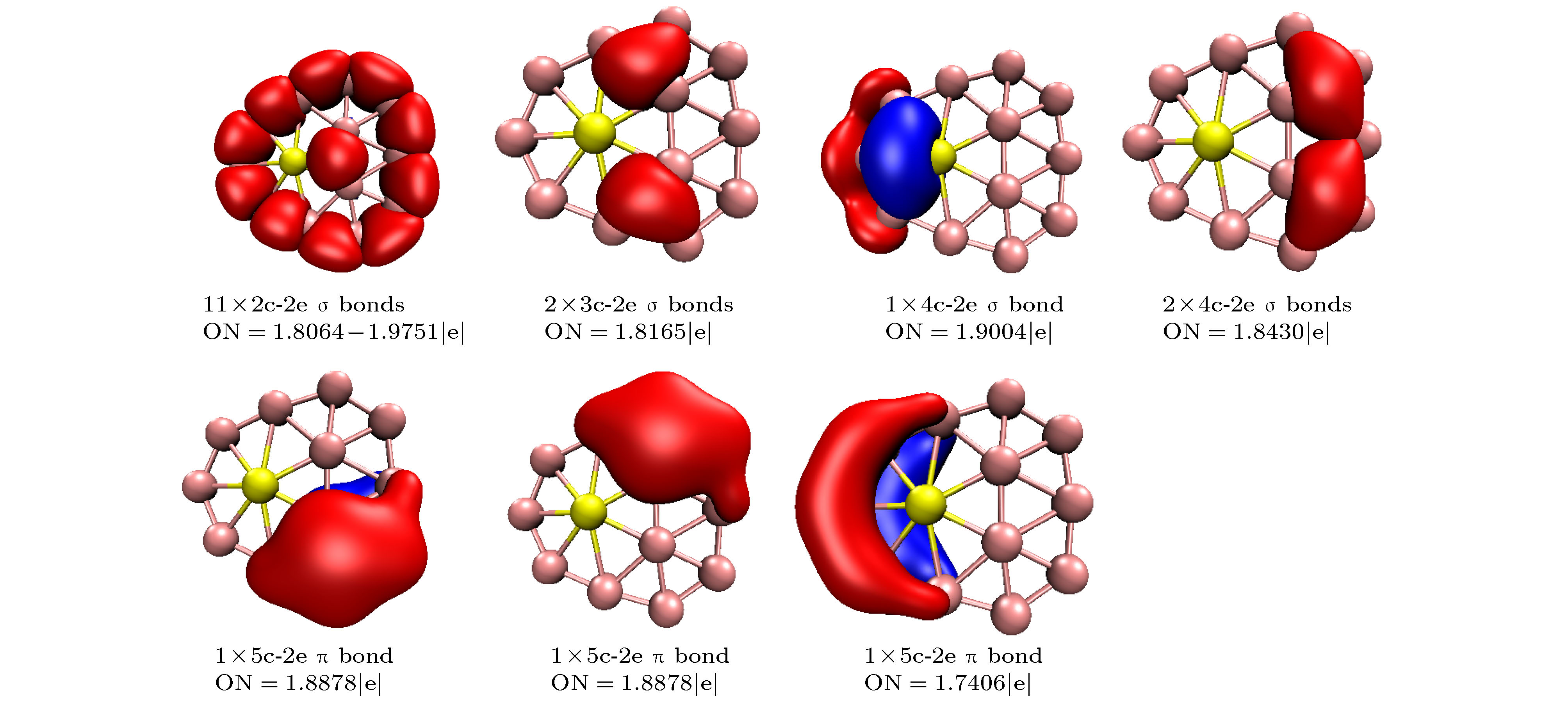
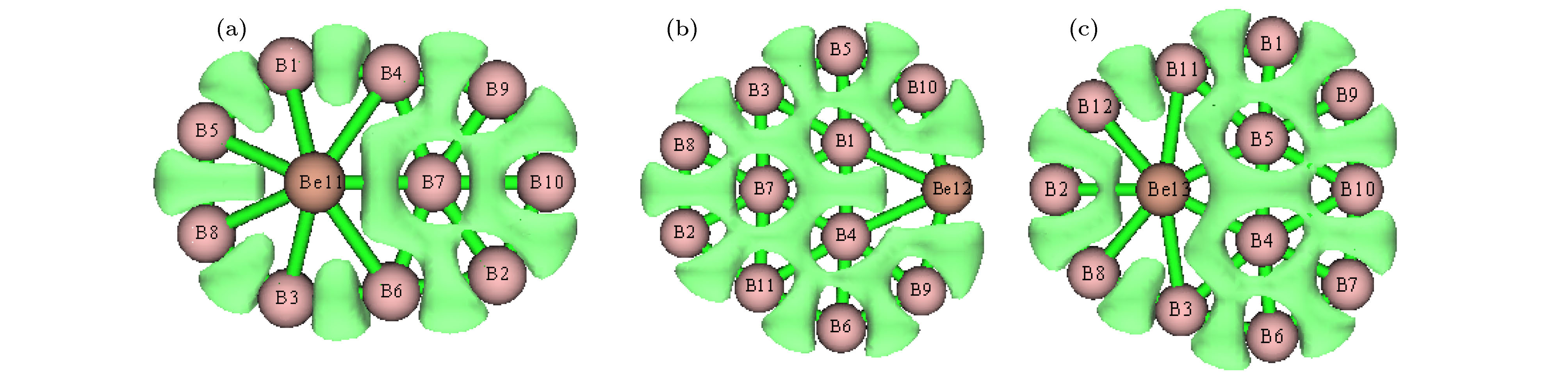
$ _{n}^{ 0/–} $ (n = 10—15)的基态几何结构; 然后采用密度泛函理论分析了最低能量结构的电子结构、极化率、红外光谱、紫外可见光谱特性. 研究结果表明: BeB$ _{10}^{ 0/–} $ , BeB$ _{11}^- $ , BeB$ _{12}^{0/−} $ , BeB$ _{14}^- $ 具有平面或准平面结构; BeB11, BeB13, BeB$ _{13}^- $ , BeB14分别具有半三明治结构、圆锥结构、笼型结构、压扁的管状结构; BeB$ _{15}^{0/−} $ 呈现手性对称结构. 自然布居分析(NPA)表明掺杂Be原子将电子转移给硼原子. 团簇的平均结合能分析可得, 阴离子比相应中性团簇的稳定性强; 另外, 随着n的增加, 中性和阴离子团簇的稳定性增强. 准平面结构BeB10, BeB$ _{11}^- $ , BeB12团簇的适应性自然密度划分(AdNDP)分析表明, σ 键促进了整个分子的稳定性, 多中心π键进一步稳定了整个分子; 另外, 这三个团簇满足6个π电子Hückel规则(4m + 2), 具有芳香性. 极化率分析可得, 平面或准平面结构的每个原子的平均极化率大于其它结构, 说明平面或准平面结构的电子离域效应较大; BeB$ _{13}^- $ , BeB$ _{14}^- $ 具有较大的第一超极化率, 说明具有较强的非线性光学响应. 红外光谱分析表明这些团簇具有不同的特征峰, 可用于鉴别这些结构; 闭壳层结构团簇的紫外可见光谱在可见光波段都有吸收峰, 开壳层结构团簇的紫外可见光谱在红外光波段都有吸收峰.A theoretical study of geometrical structures and electronic properties of Be atom doped boron clusters BeB$ _n^{0/-} $ (n = 10–15) is performed using the CALYPSO approach for the global minimum search followed by density functional theory calculations. It is found that the global minima obtained for the BeB$ _{10}^{0/-} $ , BeB$ _{11}^{-} $ , BeB$ _{12}^{0/-} $ , and BeB$ _{14}^{-} $ clusters correspond to the quasi-planar or planar structures. However, the global minima obtained for the BeB11, BeB13, BeB$ _{13}^{-} $ , BeB14 clusters correspond to the half-sandwich, cone, cage, squashed tubular structures, respectively. Interestingly, both the neutral and anionic BeB$ _{15}^{0/-} $ clusters have the axially chiral isomers which are chiral with degenerate enantiomers. Natural population analyses reveal that partial charge on Be atom transfer to boron atoms. The average binding energy values of BeB$ _n^{0/-} $ (n = 10–15) indicate that anionic clusters are overall more stable than the corresponding neutral ones, and both neutral and anionic clusters show the same trend that the stability increases gradually with the increase of B atoms number n. Chemical bonding analyses of closed-shell BeB10, BeB$ _{11}^{-} $ , BeB12 clusters reveal that the σ bonds stabilize whole molecular skeleton, and delocalized π bonds render the structure more stable. Furthermore, the three quasi-planar closed-shell clusters possess 3 delocalized π bonds, which quite surprisingly follow the 4m + 2 Hückel rule for aromaticity. Average polarizability of single atom for each quasi-planar or planar structure is larger than other structures, it indicates that quasi-planar or planar structure has stronger electron delocalization. Specifically, BeB$ _{13}^{-} $ and BeB$ _{14}^{-} $ with large first static hyperpolarizability can lead to the remarkable NLO response. The calculated spectra indicate that BeB$ _n^{0/-} $ (n = 10–15) have the meaningful characteristic peaks which can be compared with future experimental values. Our work enriches the database of geometrical structures of doped boron clusters and can provide much insight into the new doped boron clusters.[1] Kroto H W, Heath J R, O’Brien S C, Curl R F, Smalley R E 1985 Nature 318 162
Google Scholar
[2] Iijima S 1991 Nature 354 56
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Boustani I 1997 Phys. Rev. B 55 16426
Google Scholar
[5] Zhai H J, Wang L S, Alexandrova A N, Boldyrev A I 2002 J. Chem. Phys. 117 7917
Google Scholar
[6] Zhai H J, Kiran B, Li J, Wang L S 2003 Nat. Mater. 2 827
Google Scholar
[7] Kiran B, Bulusu S, Zhai H J, Yoo S, Zeng X C, Wang L S 2005 Proc. Natl. Acad. Sci. U. S. A. 102 961
Google Scholar
[8] Bean D E, Fowler P W 2009 J. Phys. Chem. C 113 15569
Google Scholar
[9] Chen Q, Wei G F, Tian W J, Bai H, Liu Z P, Zhai H J, Li S D 2014 Phys. Chem. Chem. Phys. 16 18282
Google Scholar
[10] Sergeeva A P, Popov I A, Piazza Z A, Li W L, Romanescu C, Wang L S, Boldyrev A I 2014 Acc. Chem. Res. 47 1349
Google Scholar
[11] Jian T, Chen X, Li S D, Boldyrev A I, Li J, Wang L S 2019 Chem. Soc. Rev. 48 3550
Google Scholar
[12] Piazza Z A, Hu H S, Li W L, Zhao Y F, Li J, Wang L S 2014 Nat. Commun. 5 3113
Google Scholar
[13] Casillas R, Baruah T, Zope R R 2013 Chem. Phys. Lett. 557 15
Google Scholar
[14] Pham H T, Duong L V, Pham B Q, Nguyen M T 2013 Chem. Phys. Lett. 577 32
Google Scholar
[15] Lü J, Wang Y, Zhu L, Ma Y 2014 Nanoscale 6 11692
Google Scholar
[16] Zhai H J, Zhao Y F, Li W L, Chen Q, Bai H, Hu H S, Piazza Z A, Tian W J, Lu H G, Wu Y B, Mu Y W, Wei G F, Liu Z P, Li J, Li S D, Wang L S 2014 Nat. Chem. 6 727
Google Scholar
[17] Bai H, Chen Q, Zhai H J, Li S D 2015 Angew. Chem. Int. Ed. 54 941
Google Scholar
[18] Li S X, Zhang Z P, Long Z W, Qin S J 2017 RSC Advances 7 38526
Google Scholar
[19] Dong H, Hou T, Lee S T, Li Y 2015 Sci. Rep. 5 9952
Google Scholar
[20] An Y, Zhang M, Wu D, Fu Z, Wang T, Xia C 2016 Phys. Chem. Chem. Phys. 18 12024
Google Scholar
[21] Bai H, Bai B, Zhang L, Huang W, Mu Y W, Zhai H J, Li S D 2016 Sci. Rep. 6 35518
Google Scholar
[22] Shakerzadeh E, Biglari Z, Tahmasebi E 2016 Chem. Phys. Lett. 654 76
Google Scholar
[23] Tang C, Zhang X 2016 Int. J. Hydrogen Energy 41 16992
Google Scholar
[24] Li S, Zhang Z, Long Z, Chen D 2019 ACS Omega 4 5705
Google Scholar
[25] 李世雄, 张正平, 隆正文, 秦水介 2017 66 103102
Google Scholar
Li S X, Zhang Z P, Long Z W, Qin S J 2017 Acta Phys. Sin. 66 103102
Google Scholar
[26] Popov I A, Li W L, Piazza Z A, Boldyrev A I, Wang L S 2014 J. Phys. Chem. A 118 8098
Google Scholar
[27] Liang W Y, Das A, Dong X, Cui Z H 2018 Phys. Chem. Chem. Phys. 20 16202
Google Scholar
[28] Wang W, Guo Y D, Yan X H 2016 RSC Advances 6 40155
Google Scholar
[29] Saha R, Kar S, Pan S, Martinez G G, Merino G, Chattaraj P K 2017 J. Phys. Chem. A 121 2971
Google Scholar
[30] Lü J, Wang Y, Zhu L, Ma Y 2012 J. Chem. Phys. 137 084104
Google Scholar
[31] Adamo C, Barone V 1999 J. Chem. Phys. 110 6158
Google Scholar
[32] Weigend F, Ahlrichs R 2005 Phys. Chem. Chem. Phys. 7 3297
Google Scholar
[33] Frisch M J, Trucks G W, Schlegel H B et al. 2016 Gaussian 16 (Rev. A.03). Gaussian: Inc., Wallingford CT
[34] Zubarev D Y, Boldyrev A I 2008 Phys. Chem. Chem. Phys. 10 5207
Google Scholar
[35] Lu T, Chen F 2012 J. Comput. Chem. 33 580
Google Scholar
[36] Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33
Google Scholar
[37] Cheng L 2012 J. Chem. Phys. 136 104301
Google Scholar
[38] Mayer I 1983 Chem. Phys. Lett. 97 270
Google Scholar
[39] Schmider H L, Becke A D 2000 J. Mol. Struct. THEOCHEM 527 51
Google Scholar
-
图 1 团簇结构图, 分图中上图为正面观察、下图为侧面观察 (a) BeB10; (b) BeB
$ _{10}^- $ ; (c) BeB11; (d) BeB$ _{11}^- $ ; (e) BeB12; (f) BeB$ _{12}^- $ ; (g) BeB13; (h) BeB$ _{13}^- $ ; (i) BeB14; (j) BeB$ _{14}^- $ ; (k) BeB15 I; (l) BeB$ _{15}^- $ I; (m) BeB15 II; (n) BeB$ _{15}^- $ IIFig. 1. Structures of doped boron clusters BeB
$_{n}^{ 0/–}$ (n = 10−15): (a) BeB10; (b) BeB$ _{10}^- $ ; (c) BeB11; (d) BeB$ _{11}^- $ ; (e) BeB12; (f) BeB$ _{12}^- $ ; (g) BeB13; (h) BeB$ _{13}^- $ ; (i) BeB14; (j) BeB$ _{14}^- $ ; (k) BeB15 I; (l) BeB$ _{15}^- $ I; (m) BeB15 II; (n) BeB$ _{15}^- $ II.
图 2 分子轨道图 (a) HOMO BeB10; (b) LUMO BeB10; (c) HOMO BeB
$_{11}^{-}$ ; (d) LUMO BeB$_{11}^{-}$ ; (e) HOMO BeB12; (f) LUMO BeB12; (g) HOMO BeB$_{13}^{-}$ ; (h) LUMO BeB$_{13}^{-}$ ; (i) HOMO BeB14; (j) LUMO BeB14; (k) HOMO BeB$_{15}^{-}$ I; (l) LUMO BeB$_{15}^{-}$ I; (m) HOMO BeB$_{15}^{-}$ II; (n) LUMO BeB$_{15}^{-}$ IIFig. 2. Molecular orbitals: (a) HOMO BeB10; (b) LUMO BeB10; (c) HOMO BeB
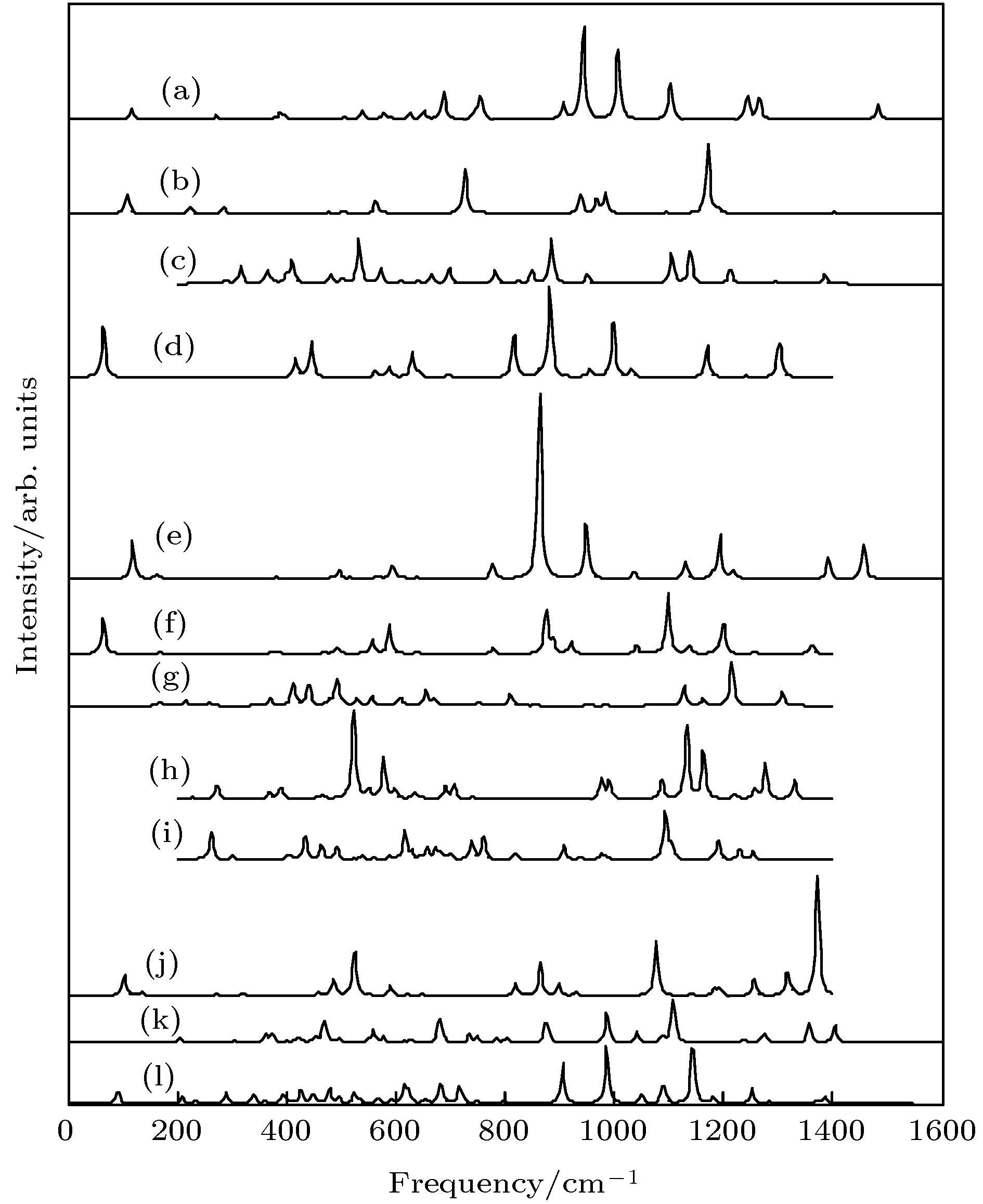
$ _{11}^- $ ; (d) LUMO BeB$ _{11}^- $ ; (e) HOMO BeB12; (f) LUMO BeB12; (g) HOMO BeB$ _{13}^- $ ; (h) LUMO BeB$ _{13}^- $ ; (i) HOMO BeB14; (j) LUMO BeB14; (k) HOMO BeB$ _{15}^- $ I; (l) LUMO BeB$_{15}^{-}$ I; (m) HOMO BeB$_{15}^{-}$ II; (n) LUMO BeB$_{15}^{-}$ II.
图 3 BeB10的AdNDP分析, ON代表占据数, 黄色球代表Be原子
Fig. 3. Bonding patterns of BeB10 from AdNDP analyses. The occupation numbers (ONs) are indicated and the yellow ball represents Be atom.
图 4 BeB
$_{11}^{-}$ 的AdNDP分析, ON代表占据数, 黄色球代表Be原子Fig. 4. Bonding patterns of BeB
$_{11}^{-}$ from AdNDP analyses. The occupation numbers (ONs) are indicated and the yellow ball represents Be atom.
图 5 BeB12的AdNDP分析, ON代表占据数, 黄色球代表Be原子
Fig. 5. Bonding patterns of BeB12 from AdNDP analyses. The occupation numbers (ONs) are indicated and the yellow ball represents Be atom.
图 6 定域化轨道函数LOL, 等值面数值为0.5 (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12Fig. 6. Localized orbital locator, the isovalue is set to 0. 5: (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12.
图 7 定域化轨道函数LOL, 等值面数值为0.56 (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12Fig. 7. Localized orbital locator, the isovalue is set to 0. 56: (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12.
图 8 定域化轨道函数LOL, 等值面数值为0.6 (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12Fig. 8. Localized orbital locator, the isovalue is set to 0.6. (a) BeB10; (b) BeB
$_{11}^{-}$ (c) BeB12.
图 9 红外光谱 (a) BeB10; (b) BeB
$_{10}^{-}$ ; (c) BeB11; (d) BeB$_{11}^{-}$ ; (e) BeB12; (f) BeB$_{12}^{-}$ ; (g) BeB13; (h) BeB$_{13}^{-}$ ; (i) BeB14; (j) BeB$_{14}^{-}$ ; (k) BeB15 I; (l) BeB$_{15}^{-}$ IFig. 9. Calculated infrared spectra: (a) BeB10; (b) BeB
$_{10}^{-}$ ; (c) BeB11; (d) BeB$_{11}^{-}$ ; (e) BeB12; (f) BeB$_{12}^{-}$ ; (g) BeB13; (h) BeB$_{13}^{-}$ ; (i) BeB14; (j) BeB$_{14}^{-}$ ; (k) BeB15 I; (l) BeB$_{15}^{-}$ I.
图 10 紫外可见光谱 (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12; (d) BeB$_{13}^{-}$ ; (e) BeB14; (f) BeB$_{15}^{-}$ IFig. 10. Calculated UV-Vis spectra: (a) BeB10; (b) BeB
$_{11}^{-}$ ; (c) BeB12; (d) BeB$_{13}^{-}$ ; (e) BeB14; (f) BeB$_{15}^{-}$ I.
图 11 紫外可见光谱 (a) BeB
$_{10}^{-}$ ; (b) BeB11; (c) BeB$_{12}^{-}$ ; (d) BeB13; (e) BeB$_{14}^{-}$ ; (f) BeB15 IFig. 11. Calculated UV-Vis spectra: (a) BeB
$_{10}^{-}$ ; (b) BeB11; (c) BeB$_{12}^{-}$ ; (d) BeB13; (e) BeB$_{14}^{-}$ ; (f) BeB15 I.表 1 BeB
$_{n}^{ 0/–}$ (n = 10—15)的几何参数Table 1. Geometrical parameters of BeB
$ _{n}^{ 0/–} $ (n = 10−15).Symmetry 最短Be—B键长/Å 结构 BeB10 Cs 1.83 准平面结构 BeB$ _{10}^- $ Cs 1.80 准平面结构 BeB11 Cs 1.97 半三明治结构 BeB$ _{11}^- $ Cs 1.86 准平面结构 BeB12 Cs 1.85 准平面结构 BeB$ _{12}^- $ C2v 1.83 平面结构 BeB13 C2v 1.93 圆锥结构 BeB$ _{13}^- $ Cs 1.80 笼型结构 BeB14 C2 1.88 压扁的管状结构 BeB$ _{14}^- $ C2 1.84 准平面结构 BeB15 I C1 1.87 三维结构 BeB15 II C1 1.87 三维结构 BeB$ _{15}^- $ I C1 1.84 三维结构 BeB$ _{15}^- $ II C1 1.84 三维结构 
下载: 导出CSV
表 2 BeB
$ _{n}^{ 0/–} $ (n = 10—15)的最低谐振频率和平均结合能Table 2. The lowest frequencies and average binding energy of BeB
$ _{n}^{ 0/–} $ (n = 10−15).BeB10 BeB$_{10}^{-}$ BeB11 BeB$ _{11}^{-} $ BeB12 BeB$ _{12}^{-} $ BeB13 BeB$ _{13}^{-} $ BeB14 BeB$ _{14}^{-} $ BeB15 I, II BeB$ _{15}^{-} $ I, II 最低谐振频率/cm–1 117 109 236 65 119 65 171 228 243 103 73 91 平均结合能/eV 4.71 5.06 4.78 5.16 4.89 5.17 4.91 5.19 4.97 5.22 4.97 5.26
下载: 导出CSV
表 3 BeB
$ _{n}^{ 0/–} $ (n = 10—15)的偶极矩, Eg, NPA电荷. 上标a, b 代表自旋向上和自旋向下电子Table 3. The dipole moments (μ), energy gaps (Eg), and NPA charges on doped atom of BeB
$ _{n}^{ 0/–} $ (n = 10−15). The markers “a” and “b” denote the alpha and beta electrons, respectively.BeB10 BeB$_{10}^{-}$ BeB11 BeB$_{11}^{-}$ BeB12 BeB$_{12}^{-}$ BeB13 BeB$_{13}^{-}$ BeB14 BeB$_{14}^{-}$ BeB15 I, II BeB$_{15}^{-}$ I, II μ/ Debye 0.80 0.58 1.49 1.59 1.31 0.66 0.22 1.12 2.57 0.86 1.95 1.88 Eg/eV 2.94 2.81a
2.63b3.10a
2.94b3.48 2.93 1.67a
3.08b2.93a
3.55b3.33 3.80 1.85a
1.99b3.23a
2.26b3.35 NPA charges
on doped atom1.62 1.64 1.56 1.37 1.64 1.66 1.72 1.60 1.69 1.68 1.70 1.67
下载: 导出CSV
表 4 BeB
$ _n^{0/-} $ (n = 10—15)的极化率Table 4. Polarizabilities of BeB
$ _n^{0/-} $ (n = 10−15).各项同性平均极化率α 每个原子的平均极化率$\bar \alpha $ 各项异性极化率Δα 第一超极化率β0 偶极矩方向上的投影值βprj BeB10 167.32 15.21 124.78 133.79 –59.10 BeB$ _{10}^- $ 196.08 17.83 142.11 216.95 –113.85 BeB11 153.17 12.76 63.19 319.45 155.00 BeB$ _{11}^- $ 203.90 16.99 139.92 233.54 199.10 BeB12 196.31 15.10 145.51 24.98 6.10 BeB$ _{12}^- $ 223.77 17.21 164.05 254.97 –254.97 BeB13 174.08 12.43 48.62 61.41 –26.71 BeB$ _{13}^- $ 210.56 15.04 119.68 941.20 –901.01 BeB14 191.44 12.76 73.13 450.89 –450.89 BeB$ _{14}^- $ 260.09 17.34 203.63 958.78 –958.78 BeB15 I 215.11 13.44 122.84 601.71 –597.78 BeB15 II 215.12 13.44 122.87 604.10 –600.31 BeB$ _{15}^- $ I 235.61 14.73 130.97 516.03 –223.98 BeB$ _{15}^- $ II 235.62 14.73 130.93 517.15 –224.33
下载: 导出CSV
表 5 BeB
$ _n^{0/-} $ (n = 10—15)的激发特性Table 5. The excitation properties of BeB
$ _n^{0/-} $ (n = 10−15).振子强度最大的激发态的波长/nm
(振子强度, 第几激发态)第一激发态的波长/nm
(振子强度)第一个吸收峰位置/nm
(对应第几激发态)BeB10 252 (0.2108, 22) 748 (0.0003) 748 (1) BeB$ _{10}^- $ 313 (0.1205, 34) 1038 (0.0001) 887 (5) BeB11 331 (0.0077, 22) 859 (0.0022) 859 (1) BeB$ _{11}^- $ 242 (0.3008, 27) 548 (0) 510 (2) BeB12 282 (0.2870, 22) 702 (0.0038) 702 (1) BeB$ _{12}^- $ 346 (0.0119, 32) 3201 (0.0003) 3201 (1) BeB13 308 (0.0377, 31) 800 (0.0015) 800 (1) BeB$ _{13}^- $ 234 (0.0875, 36) 582 (0.0003) 582 (1) BeB14 311 (0.1049, 15) 468 (0.0041) 468 (1) BeB$ _{14}^- $ 533 (0.0472, 14) 1984 (0) 982 (4—6) BeB15 I 339 (0.0295, 33) 1292 (0.0006) 1122 (1—2) BeB$ _{15}^- $ I 276 (0.0954, 24) 531 (0.0027) 531 (1)
下载: 导出CSV
-
[1] Kroto H W, Heath J R, O’Brien S C, Curl R F, Smalley R E 1985 Nature 318 162
Google Scholar
[2] Iijima S 1991 Nature 354 56
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Boustani I 1997 Phys. Rev. B 55 16426
Google Scholar
[5] Zhai H J, Wang L S, Alexandrova A N, Boldyrev A I 2002 J. Chem. Phys. 117 7917
Google Scholar
[6] Zhai H J, Kiran B, Li J, Wang L S 2003 Nat. Mater. 2 827
Google Scholar
[7] Kiran B, Bulusu S, Zhai H J, Yoo S, Zeng X C, Wang L S 2005 Proc. Natl. Acad. Sci. U. S. A. 102 961
Google Scholar
[8] Bean D E, Fowler P W 2009 J. Phys. Chem. C 113 15569
Google Scholar
[9] Chen Q, Wei G F, Tian W J, Bai H, Liu Z P, Zhai H J, Li S D 2014 Phys. Chem. Chem. Phys. 16 18282
Google Scholar
[10] Sergeeva A P, Popov I A, Piazza Z A, Li W L, Romanescu C, Wang L S, Boldyrev A I 2014 Acc. Chem. Res. 47 1349
Google Scholar
[11] Jian T, Chen X, Li S D, Boldyrev A I, Li J, Wang L S 2019 Chem. Soc. Rev. 48 3550
Google Scholar
[12] Piazza Z A, Hu H S, Li W L, Zhao Y F, Li J, Wang L S 2014 Nat. Commun. 5 3113
Google Scholar
[13] Casillas R, Baruah T, Zope R R 2013 Chem. Phys. Lett. 557 15
Google Scholar
[14] Pham H T, Duong L V, Pham B Q, Nguyen M T 2013 Chem. Phys. Lett. 577 32
Google Scholar
[15] Lü J, Wang Y, Zhu L, Ma Y 2014 Nanoscale 6 11692
Google Scholar
[16] Zhai H J, Zhao Y F, Li W L, Chen Q, Bai H, Hu H S, Piazza Z A, Tian W J, Lu H G, Wu Y B, Mu Y W, Wei G F, Liu Z P, Li J, Li S D, Wang L S 2014 Nat. Chem. 6 727
Google Scholar
[17] Bai H, Chen Q, Zhai H J, Li S D 2015 Angew. Chem. Int. Ed. 54 941
Google Scholar
[18] Li S X, Zhang Z P, Long Z W, Qin S J 2017 RSC Advances 7 38526
Google Scholar
[19] Dong H, Hou T, Lee S T, Li Y 2015 Sci. Rep. 5 9952
Google Scholar
[20] An Y, Zhang M, Wu D, Fu Z, Wang T, Xia C 2016 Phys. Chem. Chem. Phys. 18 12024
Google Scholar
[21] Bai H, Bai B, Zhang L, Huang W, Mu Y W, Zhai H J, Li S D 2016 Sci. Rep. 6 35518
Google Scholar
[22] Shakerzadeh E, Biglari Z, Tahmasebi E 2016 Chem. Phys. Lett. 654 76
Google Scholar
[23] Tang C, Zhang X 2016 Int. J. Hydrogen Energy 41 16992
Google Scholar
[24] Li S, Zhang Z, Long Z, Chen D 2019 ACS Omega 4 5705
Google Scholar
[25] 李世雄, 张正平, 隆正文, 秦水介 2017 66 103102
Google Scholar
Li S X, Zhang Z P, Long Z W, Qin S J 2017 Acta Phys. Sin. 66 103102
Google Scholar
[26] Popov I A, Li W L, Piazza Z A, Boldyrev A I, Wang L S 2014 J. Phys. Chem. A 118 8098
Google Scholar
[27] Liang W Y, Das A, Dong X, Cui Z H 2018 Phys. Chem. Chem. Phys. 20 16202
Google Scholar
[28] Wang W, Guo Y D, Yan X H 2016 RSC Advances 6 40155
Google Scholar
[29] Saha R, Kar S, Pan S, Martinez G G, Merino G, Chattaraj P K 2017 J. Phys. Chem. A 121 2971
Google Scholar
[30] Lü J, Wang Y, Zhu L, Ma Y 2012 J. Chem. Phys. 137 084104
Google Scholar
[31] Adamo C, Barone V 1999 J. Chem. Phys. 110 6158
Google Scholar
[32] Weigend F, Ahlrichs R 2005 Phys. Chem. Chem. Phys. 7 3297
Google Scholar
[33] Frisch M J, Trucks G W, Schlegel H B et al. 2016 Gaussian 16 (Rev. A.03). Gaussian: Inc., Wallingford CT
[34] Zubarev D Y, Boldyrev A I 2008 Phys. Chem. Chem. Phys. 10 5207
Google Scholar
[35] Lu T, Chen F 2012 J. Comput. Chem. 33 580
Google Scholar
[36] Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33
Google Scholar
[37] Cheng L 2012 J. Chem. Phys. 136 104301
Google Scholar
[38] Mayer I 1983 Chem. Phys. Lett. 97 270
Google Scholar
[39] Schmider H L, Becke A D 2000 J. Mol. Struct. THEOCHEM 527 51
Google Scholar
下载:
计量
- 文章访问数: 7097
- PDF下载量: 137
- 被引次数: 0
