-
纳米粒子是调控聚电解质刷行为的一种新手段, 聚电解质刷是调控纳米粒子与表面相互作用的一种重要媒介, 本文应用强拉伸理论研究了聚电解质刷浸没于带同种电荷的纳米粒子溶液中的行为. 给出了聚电解质刷、纳米粒子、反离子的密度分布和刷厚度的解析表达式, 基于解析表达式, 得到了体系的特征标度关系. 当纳米粒子浓度
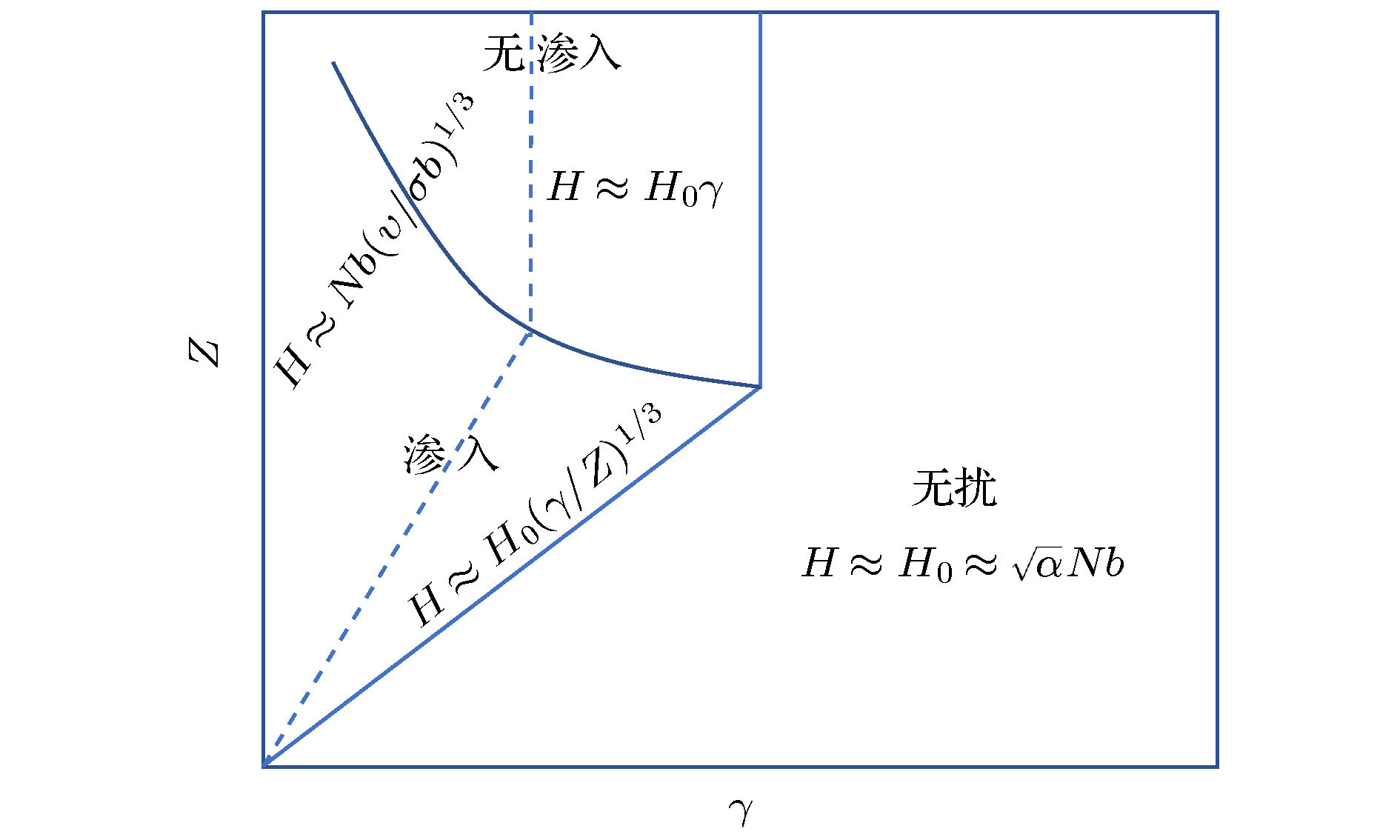
$\varPhi$ 较高, 电量Z较低时, 纳米粒子可以渗入聚电解质刷内部. 当纳米粒子浓度$\varPhi$ 相对较低, 电量Z较高时, 纳米粒子几乎不能渗入刷内部, 但依然可以影响刷的厚度. 在前一种情形下, 刷行为由反离子、纳米粒子的渗透压与链的熵弹性之间的竞争决定, 刷厚度满足的标度关系为$H \approx (Z\varPhi)^{-1/3}$ ; 在后一种情形下, 刷行为由反离子的渗透压与链的熵弹性之间的竞争决定, 刷厚度满足的标度关系为$H \approx (Z\varPhi)^{-1}$ . 本文还探究了纳米粒子多分散性的效应.Nanoparticles can be used to tune the properties of polyelectrolyte brushes, and polyelectrolyte brushes can be used to control the interaction between nanoparticles and substrates. In the present paper, we investigate the polyelectrolyte brushes immersed in a nanoparticle solution within the analytical strong-stretching theoretical framework. The theoretical model does not take the excluded volume interaction between any two components into account. When there is no nanoparticle loaded, the polyelectrolyte brush is assumed to be an osmotic brush. Local electroneutral approximation is assumed to be still valid after the nanoparticles have been loaded. The loaded nanoparticles are not big enough to deform the grafted polyelectrolyte chains laterally. Analytical formulae for density profiles of each component and brush thickness are derived. The loaded nanoparticles always compress the polyelectrolyte brush. By analyzing the limiting case, a scaling-type diagram for behaviors of the nanoparticle-loading polyelectrolyte brush is constructed. Two characteristic nanoparticle controlling regimes are shown. When the charge of the nanoparticle, Z, is not very large, charged nanoparticles penetrate into the brush and the brush thickness is scaled by$H \sim (Z\varPhi)^{-1/3}$ , where$\varPhi$ is the nanoparticle volume fraction. When the nanoparticle charge Z is large enough, nanoparticles are mainly distributed outside the brush and the brush thickness is scaled by$H \sim (Z\varPhi)^{-1}$ . In the former case, the Coulombic repulsion between the grafted polyelectrolyte chains is screened by the counterions and the nanoparticles, and the brush behavior is determined by the balance between the chain elasticity and the osmotic pressure of the counterions and the nanoparticles. In the latter case, the electrostatic screening is executed by the counterions, and the chain elasticity is balanced by the osmotic pressure of the counterions. The two regimes are divided into subregimes which are dominated respectively by electrostatic or non-electrostatic interaction. The effects of size polydispersity of the nanoparticles are also investigated. It is found that the behaviors of the grafted polyelectrolyte chains are mainly determined by the ratio between the first two moments of the nanoparticle size distribution function. The polyelectrolyte brush is compressed more by the polydispere nanoparticles than by the monodisperse ones. Possible improvement in the present theory is discussed in the conclusion section.-
Keywords:
- polyelectrolyte brush /
- strong-stretching theory /
- scaling theory /
- nanoparticle
[1] Ballauff M, Borisov O V 2006 Curr. Opin. Colloid Interface Sci. 11 316
Google Scholar
[2] Toomey R, Tirrell M 2008 Annu. Rev. Phys. Chem. 59 493
Google Scholar
[3] Rühe J, Ballauff M, Biesalski M, Dziezok P, Gröhn F, Johannsmann D, Houbenov N, Hugenberg N, Konradi R, Minko S, Motornov M, Netz R R, Schmidt M, Seidel C, Stamm M, Stephan T, Usov D, Zhan H 2004 Adv. Polym. Sci. 165 79
[4] Naji A, Seidel C, Netz R R 2006 Adv. Polym. Sci. 198 149
[5] Guenoun P 2011 Polyelectrolyte Brushes: Twenty Years After. In Functional Polymer Films (Weinheim: Wiley-VCH) pp219–237
[6] Das S, Banik M, Chen G, Sinha S, Mukherjee R 2015 Soft Matter 11 8550
Google Scholar
[7] Willott J D, Murdoch T J, Webber G B, Wanless E J 2017 Prog. Polym. Sci. 64 52
Google Scholar
[8] Chen T, Ferris R, Zhang J, Ducker R, Zauscher S 2010 Prog. Polym. Sci. 35 94
Google Scholar
[9] Zoppe J O, Ataman N C, Mocny P, Wang J, Moraes J, Klok H A 2017 Chem. Rev. 117 1105
Google Scholar
[10] Santos D E S, Li D, Ramstedt M, Gautrot J E, Soares T A 2019 Langmuir 35 5037
Google Scholar
[11] Yenice Z, Schön S, Bildirir H, Genzer J, von Klitzing R 2015 J. Phys. Chem. B 119 10348
Google Scholar
[12] Christau S, Möller T, Yenice Z, Genzer J, von Klitzing R 2014 Polymers 6 1877
Google Scholar
[13] Christau S, Möller T, Yenice Z, Genzer J, von Klitzing R 2014 Langmuir 30 13033
Google Scholar
[14] Zhu Y, Chen K, Wang X, Guo X 2012 Nanotechnology 23 265601
Google Scholar
[15] Su X, Lei Q, Ren C 2015 Chin. Phys. B 24 113601
Google Scholar
[16] Koenig M, König U, Eichhorn K J, Müller M, Stamm M, Uhlmann P 2019 Front Chem. 7 101
Google Scholar
[17] Kowalczyk S W, Kapinos L, Blosser T R, Magalhães T, van Nies P, Lim R Y, Dekker C 2011 Nat. Nanotechnol. 6 433
Google Scholar
[18] Senaratne W, Andruzzi L, Ober C K 2005 Biomacromolecules 6 2427
Google Scholar
[19] Bai H, Zhang H, He Y, Liu J, Zhang B, Wang J 2014 J. Membr. Sci. 454 220
Google Scholar
[20] Eisele N B, Frey S, Piehler J, Görlich D, Richter R P 2010 EMBO Rep. 11 366
Google Scholar
[21] Hardingham T, Mu ir, Biochim H 1972 Biophys. Acta 279 401
Google Scholar
[22] Milner S T, Witten T A, Cates M E 1988 Macromolecules 21 2610
Google Scholar
[23] Zhulina E B, Priamitsyn V A, Borisov O V 1989 Polym. Sci. USSR 31 205
Google Scholar
[24] Kim J U, O’Shaughnessy B 2002 Phys. Rev. Lett. 89 238301
Google Scholar
[25] Opferman M G, Coalson R D, Jasnow D, Zilman A 2012 Phys. Rev. E 86 031806
Google Scholar
[26] Gu C, Coalson R D, Jasnow D, Zilman A 2017 J. Phys. Chem. B 121 6425
Google Scholar
[27] Ozmaian M, Jasnow D, Eskandari Nasrabad A, Zilman A, Coalson R D 2018 J. Chem. Phys. 148 024902
Google Scholar
[28] Szleifer I 1997 Biophys. J. 72 595
Google Scholar
[29] Zhulina E B, Borisov O V 1997 J. Chem. Phys. 107 5952
[30] Zhulina E B, Borisov O V, Birshtein T M 1992 J. Phys. II France 2 63
Google Scholar
[31] Israels R, Leermakers J F A M, Fleer G J, Zhulina E B 1994 Macromolecules 27 3249
Google Scholar
[32] Borisov O V, Zhulina E B, Birshtein T M 1994 Macromolecules 27 4795
Google Scholar
-
图 1 聚电解质刷浸没于纳米粒子溶液示意图
Fig. 1. Schematic of a polyelectrolyte brush immersed in a nanoparticle solution
图 2 刷厚度
$ h $ 与接枝链电离的反离子与纳米粒子反离子体积分数之比$ \gamma $ 之间的关系. 图中所标注的$ Z $ 为纳米粒子电量Fig. 2. Dependence of brush thickness
$ h $ on the ratio of the concentrations of counterions dissociated from the grafted chains and that dissociated from the nanoparticles. The indicated$ Z $ is the quantity of the charge beard by the nanoparticle
图 3 浸没于纳米粒子溶液中的聚电解质刷标度关系示意图
Fig. 3. The scaling-type diagram of a polyelectrolyte brush loaded with nanoparticles
-
[1] Ballauff M, Borisov O V 2006 Curr. Opin. Colloid Interface Sci. 11 316
Google Scholar
[2] Toomey R, Tirrell M 2008 Annu. Rev. Phys. Chem. 59 493
Google Scholar
[3] Rühe J, Ballauff M, Biesalski M, Dziezok P, Gröhn F, Johannsmann D, Houbenov N, Hugenberg N, Konradi R, Minko S, Motornov M, Netz R R, Schmidt M, Seidel C, Stamm M, Stephan T, Usov D, Zhan H 2004 Adv. Polym. Sci. 165 79
[4] Naji A, Seidel C, Netz R R 2006 Adv. Polym. Sci. 198 149
[5] Guenoun P 2011 Polyelectrolyte Brushes: Twenty Years After. In Functional Polymer Films (Weinheim: Wiley-VCH) pp219–237
[6] Das S, Banik M, Chen G, Sinha S, Mukherjee R 2015 Soft Matter 11 8550
Google Scholar
[7] Willott J D, Murdoch T J, Webber G B, Wanless E J 2017 Prog. Polym. Sci. 64 52
Google Scholar
[8] Chen T, Ferris R, Zhang J, Ducker R, Zauscher S 2010 Prog. Polym. Sci. 35 94
Google Scholar
[9] Zoppe J O, Ataman N C, Mocny P, Wang J, Moraes J, Klok H A 2017 Chem. Rev. 117 1105
Google Scholar
[10] Santos D E S, Li D, Ramstedt M, Gautrot J E, Soares T A 2019 Langmuir 35 5037
Google Scholar
[11] Yenice Z, Schön S, Bildirir H, Genzer J, von Klitzing R 2015 J. Phys. Chem. B 119 10348
Google Scholar
[12] Christau S, Möller T, Yenice Z, Genzer J, von Klitzing R 2014 Polymers 6 1877
Google Scholar
[13] Christau S, Möller T, Yenice Z, Genzer J, von Klitzing R 2014 Langmuir 30 13033
Google Scholar
[14] Zhu Y, Chen K, Wang X, Guo X 2012 Nanotechnology 23 265601
Google Scholar
[15] Su X, Lei Q, Ren C 2015 Chin. Phys. B 24 113601
Google Scholar
[16] Koenig M, König U, Eichhorn K J, Müller M, Stamm M, Uhlmann P 2019 Front Chem. 7 101
Google Scholar
[17] Kowalczyk S W, Kapinos L, Blosser T R, Magalhães T, van Nies P, Lim R Y, Dekker C 2011 Nat. Nanotechnol. 6 433
Google Scholar
[18] Senaratne W, Andruzzi L, Ober C K 2005 Biomacromolecules 6 2427
Google Scholar
[19] Bai H, Zhang H, He Y, Liu J, Zhang B, Wang J 2014 J. Membr. Sci. 454 220
Google Scholar
[20] Eisele N B, Frey S, Piehler J, Görlich D, Richter R P 2010 EMBO Rep. 11 366
Google Scholar
[21] Hardingham T, Mu ir, Biochim H 1972 Biophys. Acta 279 401
Google Scholar
[22] Milner S T, Witten T A, Cates M E 1988 Macromolecules 21 2610
Google Scholar
[23] Zhulina E B, Priamitsyn V A, Borisov O V 1989 Polym. Sci. USSR 31 205
Google Scholar
[24] Kim J U, O’Shaughnessy B 2002 Phys. Rev. Lett. 89 238301
Google Scholar
[25] Opferman M G, Coalson R D, Jasnow D, Zilman A 2012 Phys. Rev. E 86 031806
Google Scholar
[26] Gu C, Coalson R D, Jasnow D, Zilman A 2017 J. Phys. Chem. B 121 6425
Google Scholar
[27] Ozmaian M, Jasnow D, Eskandari Nasrabad A, Zilman A, Coalson R D 2018 J. Chem. Phys. 148 024902
Google Scholar
[28] Szleifer I 1997 Biophys. J. 72 595
Google Scholar
[29] Zhulina E B, Borisov O V 1997 J. Chem. Phys. 107 5952
[30] Zhulina E B, Borisov O V, Birshtein T M 1992 J. Phys. II France 2 63
Google Scholar
[31] Israels R, Leermakers J F A M, Fleer G J, Zhulina E B 1994 Macromolecules 27 3249
Google Scholar
[32] Borisov O V, Zhulina E B, Birshtein T M 1994 Macromolecules 27 4795
Google Scholar
下载:
计量
- 文章访问数: 6190
- PDF下载量: 63
- 被引次数: 0
