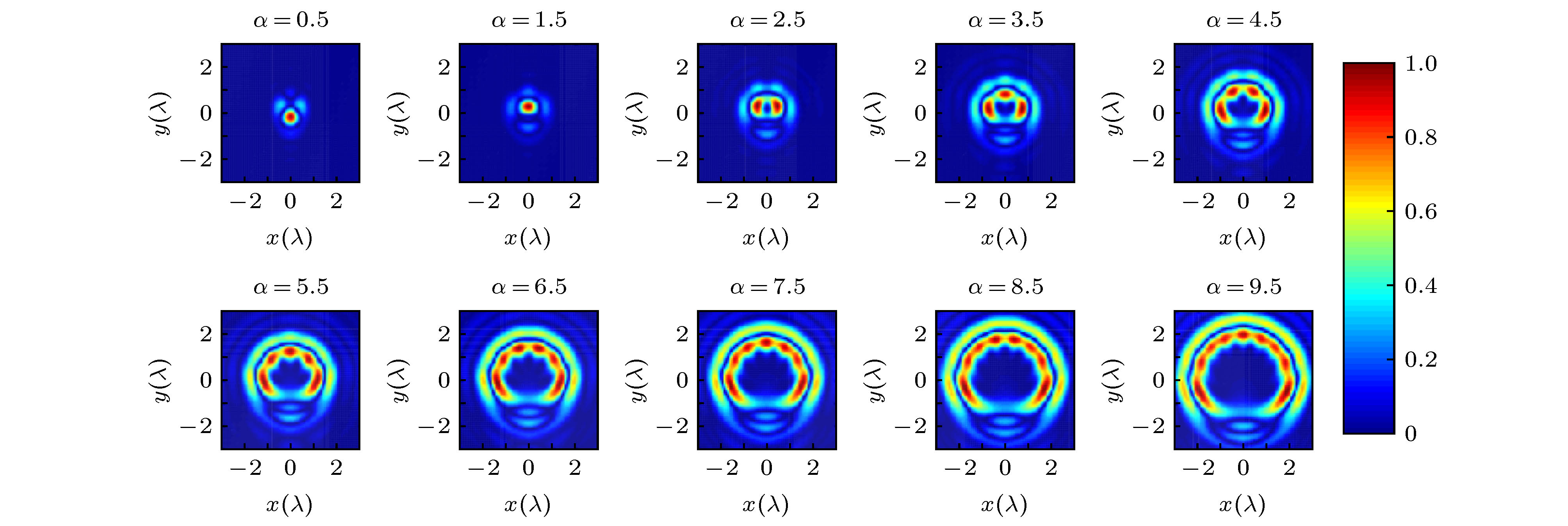
-
基于理查德-沃尔夫矢量衍射理论和逆法拉第效应, 首次推导出紧聚焦角向偏振分数阶涡旋光诱导磁化场表达式, 分析出角向偏振分数阶涡旋光诱导磁化场可近似等效为有限个相邻整数阶涡旋角向偏振光诱导磁化场与其交叉诱导磁化场的加权叠加. 数值模拟了紧聚焦条件下不同分数阶涡旋角向偏振光诱导磁化场的分布特性. 模拟结果表明角向偏振分数阶涡旋光诱导磁化场呈非对称分布. 当取分数阶涡旋拓扑荷
$ \alpha \in {{[0}}{{.5,1}}{{.5]}} $ 时, 随着涡旋拓扑荷的增加, 磁化场横向平面分布出现分裂现象, 同时还引起磁斑垂直于光轴方向的自移效应. 当$ \alpha=0.5 $ 或1.5时, 磁斑中心最大偏移量达$0.24\lambda $ ; 当分数阶涡旋拓扑荷$ \alpha \in (2,3] $ 时, 磁化场横向平面分布分裂出2个强度热点, 强度分布环径逐渐变大. 当分数阶涡旋拓扑荷趋于$ \alpha=3 $ 整数时, 磁化场横向平面分布也趋于圆对称性分布. 特别有趣的是, 当分数阶涡旋拓扑荷取半整数, 尤其大于3时, 磁化场强度热点数与其包围的暗点数均与涡旋阶数存在正相关关系, 其中热点数为$ \alpha-0.5 $ , 暗点数为$\alpha-1.5 $ . 这些研究结果将可应用于全光磁记录和磁性粒子的捕获与操控等.All-optical magnetic recording based on the inverse Faraday effect has become a research hotspot in recent years due to its ultra-high storage density and ultra-fast magnetization reversal rate. Existing studies have shown that by optimizing the phase modulation or performing 4π tight focusing of azimuthally polarized vortex beams, high-resolution longitudinal magnetization fields with different axisymmetric intensity patterns can be generated. In order to meet the requirements of more complex all-optical magnetic recording and asymmetric magnetic particle capture and manipulation, it is particularly important to generate an asymmetric light-induced magnetization field with adjustable center position. Studies have shown that the fractional vortex phase could lead to the asymmetric focal field distribution generation under tight focusing conditions, which means that the tightly-focused azimuthally polarized light carrying the fractional vortex phase can produce a novel asymmetric light-induced magnetization field. As a new degree of freedom for the regulation of the magnetization field, the fractional topological charge will bring more new phenomena, new effects and new applications in the field of interaction between light and matter. In this work, for the first time to our knowledge, the magnetization induced by tightly focused azimuthally polarized fractional vortex beam is studied based on the Richard-Wolf vector diffraction theory and the inverse Faraday effect. The equivalent approximation of the magnetization induced by azimuthally polarized fractional vortex beam regarded as a weighted superposition of magnetization induced and crossly induced by a finite number of azimuthally polarized adjacent integer-order vortex beams, where the number of the equivalent terms is chosen by using the histogram intersection method of the intensity distribution image of the magnetization field. The magnetization field distribution under different values of α are also numerically simulated. Studies have shown that magnetization induced by the azimuthally polarized fractional vortex beam is asymmetrically distributed. When the fractional vortex topological charge α belongs to [0.5,1.5], as the vortex topological load increases, the splitting phenomenon of the transverse distribution of magnetization field appears with the magnetization spot position shift in the direction perpendicular to the optical axis. When α equals 0.5 or 1.5, the maximum offset of the center of the magnetization spot is 0.24λ. When the fractional vortex topological charge α belongs to [2,3], the transverse distribution of magnetization field splits two hot intensity spots with gradually growing outer ring diameter. When the fractional vortex topological charge α tends to be an integer 3, the transverse distribution of magnetization field also gets round and symmetrical. In particular, when the fractional vortex topological charge α is a half-integer, especially larger than 3. The number of hot spots ($\alpha - 0.5 $ ) of the intensity of the magnetization field and the number of dark spots ($ \alpha - 1.5 $ ) surrounded by them all have a positive correlation with the number of vortex order. The research in this paper is expected to have new applications in the fields of all-optical magnetic recording and the capture and manipulation of magnetic particles.-
Keywords:
- asymmetric distribution /
- fractional vortex /
- inverse Faraday effect /
- tight focus
[1] Pitaevskii L P 1961 Sov. Phys. JETP 12 5
[2] Pershan P S 1963 Phys. Rev. 130 919
[3] Weller D, Moser A 1999 IEEE Trans. Magn. 35 4423
Google Scholar
[4] Wang S C, Li X P, Zhou J Y, Gu M 2015 Opt. Express 23 13530
Google Scholar
[5] Zhang Y, Okuno Y, Xu X 2009 J. Opt. Soc. Am. B 26 7
[6] Zhan Q W 2009 Adv. Opt. Photon. 1 1
Google Scholar
[7] Jiang Y S, Li X P, Gu M 2013 Opt. Lett. 38 2957
Google Scholar
[8] Gong L P, Wang L, Zhu Z Q, Wang X L, Zhao H, Gu B 2016 Appl. Opt. 55 5783
Google Scholar
[9] Nie Z Q, Ding W Q, Shi G, Li D Y, Zhang X R, Wang Y X, Song Y L 2015 Opt. Express 23 21296
Google Scholar
[10] Wang S C, Li X P, Zhou J Y, Gu M 2014 Opt. Lett. 39 5022
Google Scholar
[11] Coullet P, Gil L, Rocca F 1989 Opt. Commun. 73 403
Google Scholar
[12] Berry V M 2004 J. Opt. A-Pure Appl. Op. 6 259
Google Scholar
[13] Leach J, Yao E, Padgett J M 2004 New J. Phys. 6 71
Google Scholar
[14] Gbur G 2016 Optica 3 222
Google Scholar
[15] 李阳月, 陈子阳, 刘辉, 蒲继雄 2010 59 1740
Google Scholar
Li Y Y, Chen Z Y, Liu H, Pu J X 2010 Acta Phys. Sin. 59 1740
Google Scholar
[16] 方桂娟, 孙顺红, 蒲继雄 2012 61 064210
Google Scholar
Fang G J, Sun S H, Pu J X 2012 Acta Phys. Sin. 61 064210
Google Scholar
[17] Zhang N, Davis J A, Moreno I, Lin J, Moh K J, Cottrell D M, Yuan X C 2010 Appl. Opt. 49 2456
Google Scholar
[18] Zhu J, Zhang P, Fu D Z, Chen D X, Liu R F, Zhou Y N, Gao H, Li F L 2016 Photon. Res. 4 187
Google Scholar
[19] Wen J S, Wang L G, Yang X H, Zhang J X, Zhu S Y 2019 Opt. Express 27 5893
Google Scholar
[20] Liu C X, Chew K H, Wu Y, Chen R P 2020 J. Opt. Soc. Am. A 37 327
Google Scholar
[21] Tao S H, Yuan X C, Lin J, Peng X, Niu H B 2005 Opt. Express 13 7726
Google Scholar
[22] Guo C S, Yu Y N, Hong Z P 2010 Opt. Commun. 283 1889
Google Scholar
[23] Du F R, Zhou Z H, Tan Q F, Yang C X, Zhang X Q, Zhu L Q 2013 Chin. Phys. B. 22 064202
Google Scholar
[24] 李新忠, 台玉萍, 李贺贺, 王静鸽, 聂兆刚, 汤洁, 王辉, 尹传磊 2016 中国激光 43 0605002
Google Scholar
Li X Z, Tai Y P, Li H H, Wang J G, Nie Z G, Tang J, Wang H, Yin C L 2016 Chin. J. Las. 43 0605002
Google Scholar
[25] Xu H F, Zhang R, Sheng Z Q, Qu J 2019 Opt. Express 27 23959
Google Scholar
[26] Vetsch E, Reitz D, Sagué G, Schmidt R, Dawkins S T, Rauschenbeutel A 2010 Phys. Rev. Lett. 104 203603
Google Scholar
[27] Richards B, Wolf E 1959 Proc. Roy. Soc. A. 253 1274
[28] Youngworth K S, Brown T G 2000 Opt. Express 7 77
Google Scholar
[29] Hertel R 2006 J. Magn. Magn. Mater. 303 L1
[30] 米兰·桑卡, 瓦茨拉夫, 罗杰·博伊尔 著 (艾海舟, 武勃 译) 2003 图像处理、分析与机器视觉(北京: 清华大学出版社) 第21−127页
Sonka M, Hlavac V, Boyle R (translated by Ai H Z, Wu B) 2003 Image Processing, Analysis, And Machine Vision (Beijing: Tsinghua University Press) pp21−127 (in Chinese)
[31] 加里·布拉德斯基, 阿德里安·凯布勒 著 (于仕琪, 刘瑞祯 译 2009 学习Open CV[M]. (北京: 清华大学出版社) 第155−279页
Bradski G, Kaebler A (translated by Yu S Q, Liu R Z) 2009 Learn Open CV [M] (Beijing: Tsinghua University Press) pp155−279 (in Chinese)
-
图 1 紧聚焦光诱导磁化场原理图.
$P\left( {{\rho _s}, {\phi _s}, {z_s}} \right)$ 是焦平面中的观察点Fig. 1. Schematic diagram of magnetization induced by a tightly focused beam.
$P\left( {{\rho _s}, {\phi _s}, {z_s}} \right)$ is the observation point in the focal plane.
图 2 当
$\alpha = 1.3$ 时不同等效项数($n'$ )下的磁化场强度分布图相似度比较图Fig. 2. Comparison diagram of the similarity of the magnetization intensity distribution under different equivalent terms when
$\alpha = 1.3$ .
图 3 不同
$\alpha $ 情况下磁化场强度分布(x-y平面和x-z平面)、z = 0截面强度及其峰值位置偏移图Fig. 3. Magnetization Distribution (x-y plane and y-z plane) with the intensity line scan at z = 0 and its peak position offset under different values of
$\alpha $ .
图 4 不同
$\alpha $ 情况下磁化场横向分布强度分布图(x-y平面)Fig. 4. Transverse magnetization distribution (x-y plane) under different values of
$\alpha $ cases.
图 5 不同
$\alpha $ 情况下紧聚焦角向偏振半整数阶涡旋光诱导磁化场的分布Fig. 5. Magnetization distribution induced by tightly focused azimuthally polarized beam with semi-integer order vortex under different values of
$\alpha $ . -
[1] Pitaevskii L P 1961 Sov. Phys. JETP 12 5
[2] Pershan P S 1963 Phys. Rev. 130 919
[3] Weller D, Moser A 1999 IEEE Trans. Magn. 35 4423
Google Scholar
[4] Wang S C, Li X P, Zhou J Y, Gu M 2015 Opt. Express 23 13530
Google Scholar
[5] Zhang Y, Okuno Y, Xu X 2009 J. Opt. Soc. Am. B 26 7
[6] Zhan Q W 2009 Adv. Opt. Photon. 1 1
Google Scholar
[7] Jiang Y S, Li X P, Gu M 2013 Opt. Lett. 38 2957
Google Scholar
[8] Gong L P, Wang L, Zhu Z Q, Wang X L, Zhao H, Gu B 2016 Appl. Opt. 55 5783
Google Scholar
[9] Nie Z Q, Ding W Q, Shi G, Li D Y, Zhang X R, Wang Y X, Song Y L 2015 Opt. Express 23 21296
Google Scholar
[10] Wang S C, Li X P, Zhou J Y, Gu M 2014 Opt. Lett. 39 5022
Google Scholar
[11] Coullet P, Gil L, Rocca F 1989 Opt. Commun. 73 403
Google Scholar
[12] Berry V M 2004 J. Opt. A-Pure Appl. Op. 6 259
Google Scholar
[13] Leach J, Yao E, Padgett J M 2004 New J. Phys. 6 71
Google Scholar
[14] Gbur G 2016 Optica 3 222
Google Scholar
[15] 李阳月, 陈子阳, 刘辉, 蒲继雄 2010 59 1740
Google Scholar
Li Y Y, Chen Z Y, Liu H, Pu J X 2010 Acta Phys. Sin. 59 1740
Google Scholar
[16] 方桂娟, 孙顺红, 蒲继雄 2012 61 064210
Google Scholar
Fang G J, Sun S H, Pu J X 2012 Acta Phys. Sin. 61 064210
Google Scholar
[17] Zhang N, Davis J A, Moreno I, Lin J, Moh K J, Cottrell D M, Yuan X C 2010 Appl. Opt. 49 2456
Google Scholar
[18] Zhu J, Zhang P, Fu D Z, Chen D X, Liu R F, Zhou Y N, Gao H, Li F L 2016 Photon. Res. 4 187
Google Scholar
[19] Wen J S, Wang L G, Yang X H, Zhang J X, Zhu S Y 2019 Opt. Express 27 5893
Google Scholar
[20] Liu C X, Chew K H, Wu Y, Chen R P 2020 J. Opt. Soc. Am. A 37 327
Google Scholar
[21] Tao S H, Yuan X C, Lin J, Peng X, Niu H B 2005 Opt. Express 13 7726
Google Scholar
[22] Guo C S, Yu Y N, Hong Z P 2010 Opt. Commun. 283 1889
Google Scholar
[23] Du F R, Zhou Z H, Tan Q F, Yang C X, Zhang X Q, Zhu L Q 2013 Chin. Phys. B. 22 064202
Google Scholar
[24] 李新忠, 台玉萍, 李贺贺, 王静鸽, 聂兆刚, 汤洁, 王辉, 尹传磊 2016 中国激光 43 0605002
Google Scholar
Li X Z, Tai Y P, Li H H, Wang J G, Nie Z G, Tang J, Wang H, Yin C L 2016 Chin. J. Las. 43 0605002
Google Scholar
[25] Xu H F, Zhang R, Sheng Z Q, Qu J 2019 Opt. Express 27 23959
Google Scholar
[26] Vetsch E, Reitz D, Sagué G, Schmidt R, Dawkins S T, Rauschenbeutel A 2010 Phys. Rev. Lett. 104 203603
Google Scholar
[27] Richards B, Wolf E 1959 Proc. Roy. Soc. A. 253 1274
[28] Youngworth K S, Brown T G 2000 Opt. Express 7 77
Google Scholar
[29] Hertel R 2006 J. Magn. Magn. Mater. 303 L1
[30] 米兰·桑卡, 瓦茨拉夫, 罗杰·博伊尔 著 (艾海舟, 武勃 译) 2003 图像处理、分析与机器视觉(北京: 清华大学出版社) 第21−127页
Sonka M, Hlavac V, Boyle R (translated by Ai H Z, Wu B) 2003 Image Processing, Analysis, And Machine Vision (Beijing: Tsinghua University Press) pp21−127 (in Chinese)
[31] 加里·布拉德斯基, 阿德里安·凯布勒 著 (于仕琪, 刘瑞祯 译 2009 学习Open CV[M]. (北京: 清华大学出版社) 第155−279页
Bradski G, Kaebler A (translated by Yu S Q, Liu R Z) 2009 Learn Open CV [M] (Beijing: Tsinghua University Press) pp155−279 (in Chinese)
下载:
计量
- 文章访问数: 6894
- PDF下载量: 143
- 被引次数: 0
