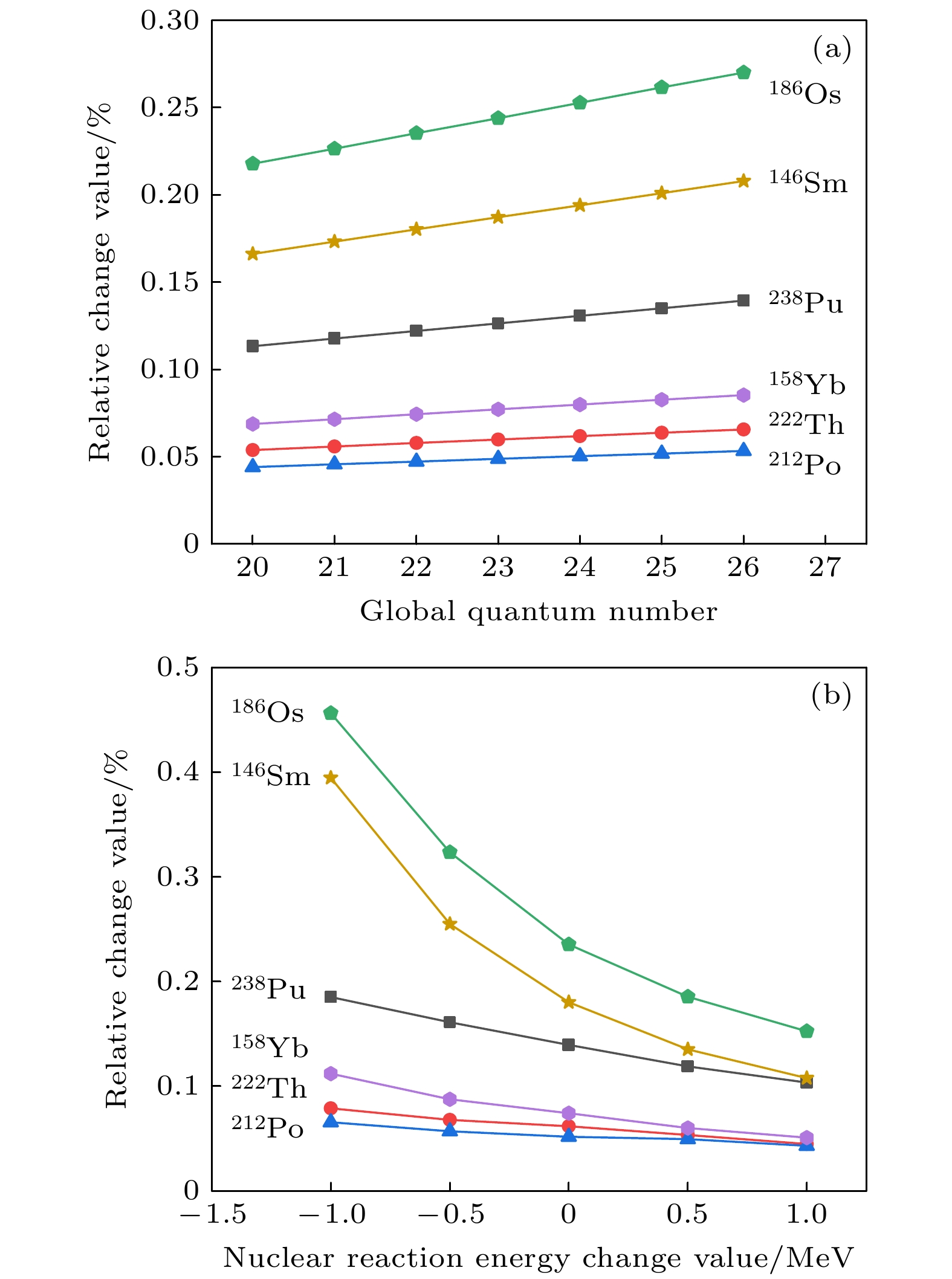
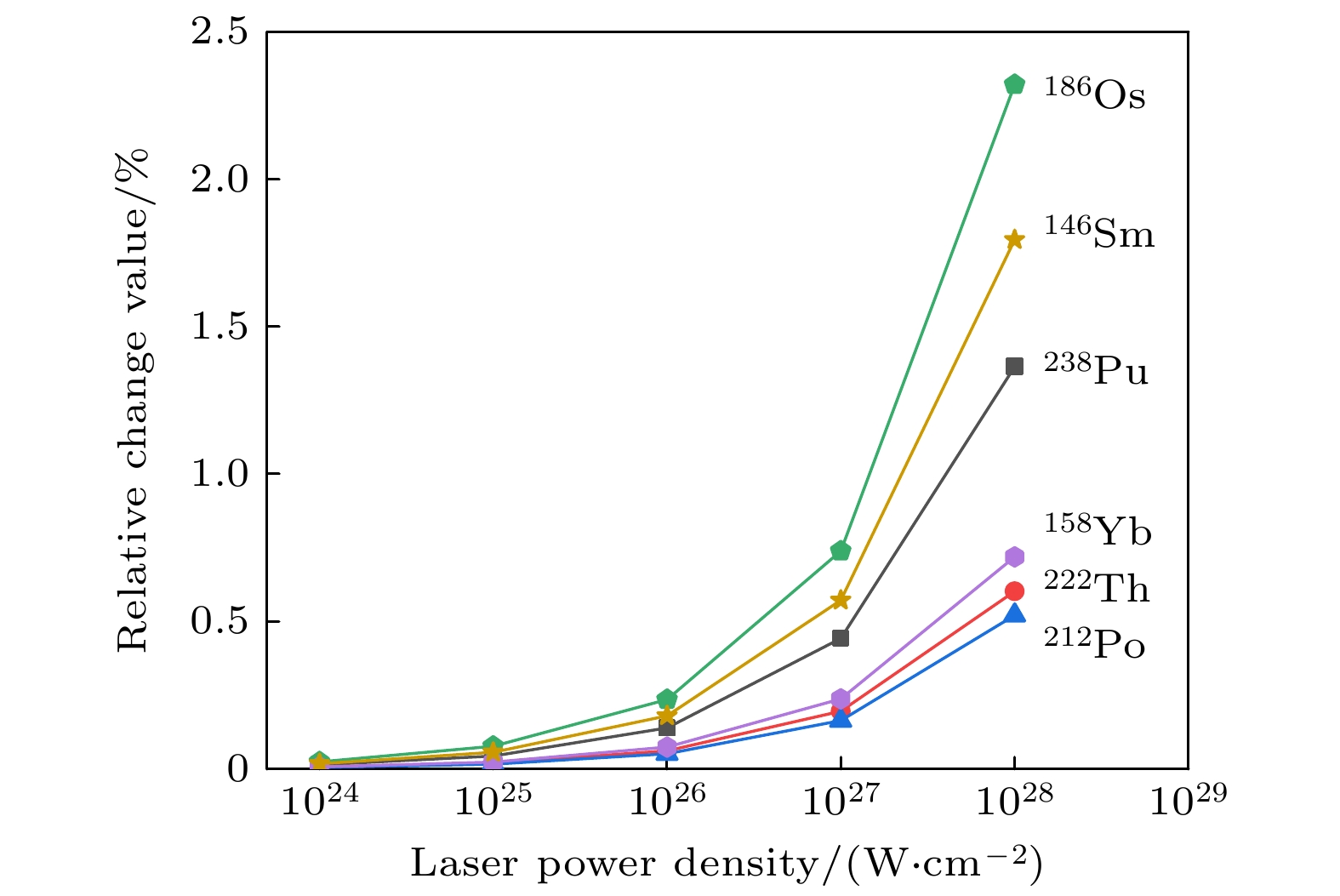
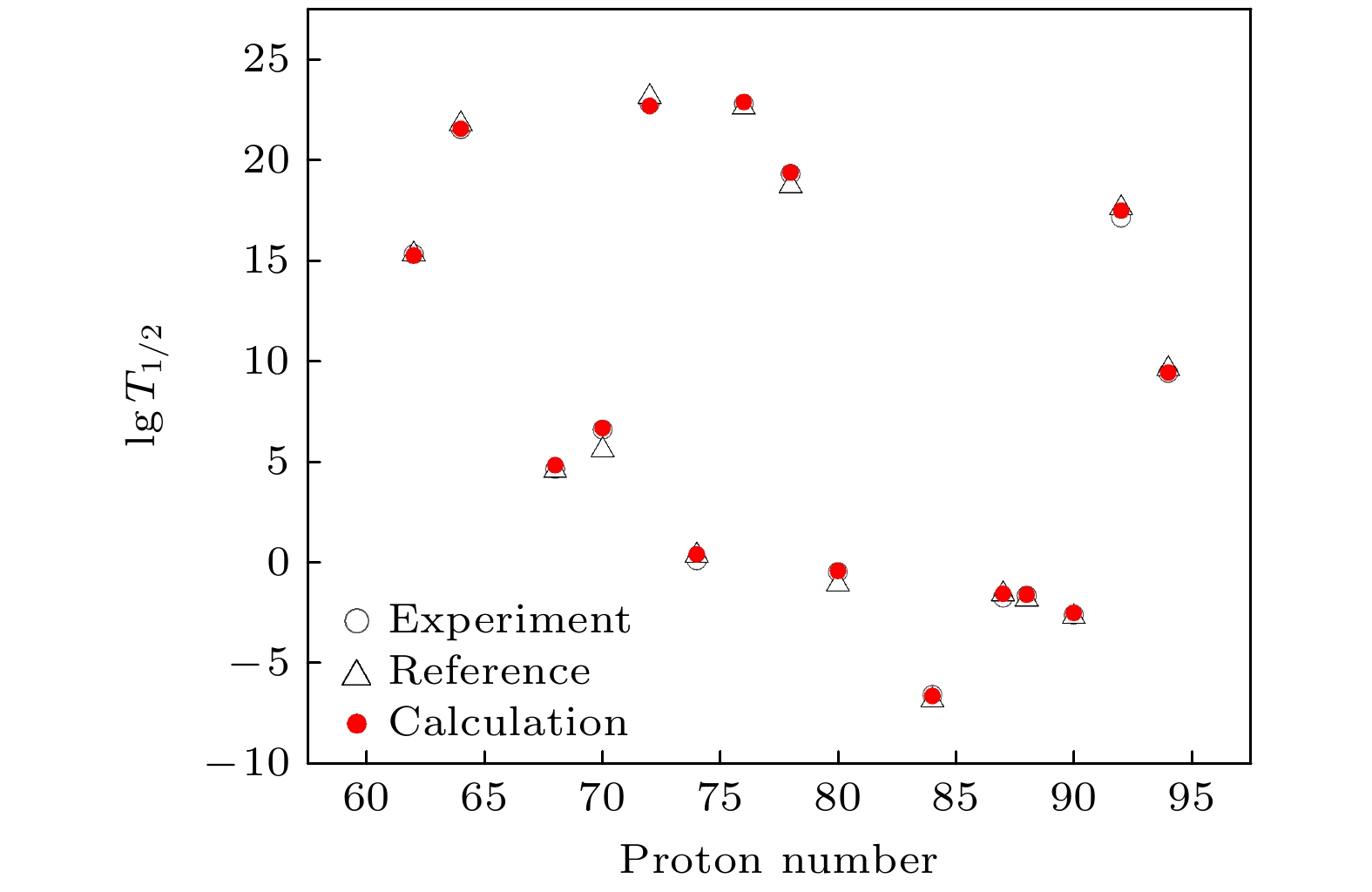
-
With the development of pulse amplification and compression technology, the peak power of the pulse has been improved by several orders of magnitude, and it is possible for the ultra strong laser field to affect nuclei directly. The α decay, as one of the most major forms in nuclear reaction, is a critical research topic in nuclear physics. According to the theory of Gamow model explaining nuclear α decay in quantum mechanics, double folding model solving nuclear potential energy, and cluster model describing atomic nucleus, we present a complete set of solutions for the half-life of nuclear α decay to study the influence of ultra strong laser field on nuclear α decay. These half-lives of α decay of different nuclei from medium to heavy in the absence of laser field are obtained, which accord well with the experimental data. Subsequently, we introduce the effects of ultra strong laser field into our theoretical method to achieve the variations of the half-life of nuclear α decay. Considering that the optical period of the laser pulse is much longer than the theoretical tunneling time and the Lorentz force is much smaller than the Coulomb force, the laser field is treated as an electrostatic field. The results show that the half-life of nuclear α decay will reduce about 0.1% by the strong laser field with a peak power density of about 1.0×1026 W/cm2, demonstrating that the half-life of nuclear α decay is effectively affected by the strong laser field. Furthermore, the influences of the nuclear parameters, e.g. total quantum number G describing α particle orbits, and α decay reaction energy Qα, on the variations of these half-lives of α decay of different nuclei are discussed with the help of the calculation results. The dependence of the half-lives of nuclear α decay on the laser peak power density is also explained correspondingly. In summary, we provide a more accurate method of calculating the half-life of nuclear α decay, which is used to study the influences of ultra strong laser field on these half-lives of nuclear α decay of different nuclei. With the further construction of strong laser devices, more interesting phenomena and results will be found from the experiment on the atomic nucleus under strong laser field.
-
Keywords:
- strong laser /
- α decay /
- half-life
[1] Gamow G 1928 Z. Phys. 51 204
Google Scholar
[2] Gurney R W, Condon E U 1929 Phys. Rev. 33 127
Google Scholar
[3] Yahya W A, Kimene Kaya B D C 2022 Int. J. Mod. Phys. E 31 2250002
[4] Gontchar I I, Chushnyakova M V 2010 Comput. Phys. Commun. 181 168
Google Scholar
[5] Deng J G, Zhao J C, Chu P C, Li X H 2018 Phys. Rev. C 97 044322
Google Scholar
[6] 邓军刚 2022 博士学位论文 (兰州: 兰州大学)第27—44页
Deng J G 2022 Ph. D. Dissertation (Lanzhou: Lanzhou University) pp27–44
[7] Qian Y, Ren Z 2014 Phys. Lett. B 738 87
Google Scholar
[8] Mourou G 2019 Rev. Mod. Phys. 91 030501
Google Scholar
[9] 沈百飞, 吉亮亮, 张晓梅, 步志刚, 徐建彩 2021 70 084101
Google Scholar
Shen B F, Ji L L, Zhang X M, Bu Z G, Xu J C 2021 Acta Phys. Sin. 70 084101
Google Scholar
[10] Ledingham K W D, Spencer I, McCanny T, Singhal R P, Santala M I K, Clark E, Watts I, Beg F N, Zepf M, Krushelnick K, Tatarakis M, Dangor A E, Norreys P A, Allott R, Neely D, Clark R J, Machacek A C, Wark J S, Cresswell A J, Sanderson D C W, Magill J 2000 Phys. Rev. Lett. 84 899
Google Scholar
[11] 席晓峰, 郭冰, 符长波, 吕冲, 张国强 2023 原子能科学技术 57 865
Google Scholar
Xi X F, Guo B, Fu C B, Lü C, Zhang G Q 2023 At. Energy Sci. Technol. 57 865
Google Scholar
[12] Castañeda Cortés H M 2012 Ph. D. Dissertation (Heidelberg: Ruprecht-Karls-Universität) pp69–103
[13] Buck B, Merchant A C, Perez S M 1990 Phys. Rev. Lett. 65 2975
Google Scholar
[14] Qi J T, Li T, Xu R H, Fu L B, Wang X 2019 Phys. Rev. C 99 044610
Google Scholar
[15] Delion D S, Ghinescu S A 2017 Phys. Rev. Lett. 119 202501
Google Scholar
[16] Wang X 2020 Phys. Rev. C 102 011601
Google Scholar
[17] Qi J 2022 Nucl. Phys. A 1020 122394
Google Scholar
[18] Qi J, Fu L 2020 Phys. Rev. C 102 064629
Google Scholar
[19] Pálffy A, Popruzhenko S V 2020 Phys. Rev. Lett. 124 212505
Google Scholar
[20] Cortés H C, Popruzhenko S V, Bauer D, Pálffy A 2011 New J. Phys. 13 063007
Google Scholar
[21] Queisser F, Schützhold R 2019 Phys. Rev. C 100 041601
[22] Ur C A, Balabanski D, Cata-Danil G, Gales S, Morjan I, Tesileanu O, UrsescuD, Ursu I, Zamfir N V 2015 Nucl. Instrum. Methods Phys. Res., Sect. B 355 198
Google Scholar
[23] Balabanski D L, Constantin P, Rotaru A, State A 2019 Hyperfine Interact. 240 49
Google Scholar
[24] Zhang Z X, Wu F X, Hu J B, Yang X J, Gui J Y, Ji P H, Liu X Y, Wang C, Liu Y Q, Lu X M, Xu Y, Leng Y X, Li R X, Xu Z Z 2020 High Power Laser Sci. Eng. 8 e4
Google Scholar
[25] Li W Q, Gan Z B, Yu L H, Wang C, Liu Y Q, Guo Z, Xu L, Xu M, Hang Y, Xu Y, Wang J Y, Huang P, Cao H, Yao B, Zhang X B, Chen L R, Tang Y H, Li S, Liu X Y, Li S M, He M Z, Yin D J, Liang X Y, Leng Y X, Li R X, Xu Z Z 2018 Opt. Lett. 43 5681
Google Scholar
[26] Buck B, Merchant A C, Perez S M 1991 J. Phys. G: Nucl. Part. Phys. 17 1223
[27] Bertsch G, Borysowicz J, McManus H, Love W G 1977 Nucl. Phys. A 284 399
Google Scholar
[28] Wildermuth K, Kanellopoulos T 1958 Nucl. Phys. 7 150
Google Scholar
[29] 卢希庭 2000 原子核物理 (修订版) (北京: 原子能出版社) 第22页
Lu X T 2000 Nuclear Physics (Rev. Ed.) (Beijing: Atomic Energy Publishing House) p22
[30] Jeffreys H 1925 Proceedings of the London Mathematical Society s2-23 428
Google Scholar
[31] 邢凤竹, 崔建坡, 王艳召, 顾建中 2022 71 062301
Google Scholar
Xing F Z, Cui J P, Wang Y Z, Gu J Z 2022 Acta Phys. Sin. 71 062301
Google Scholar
[32] Maroufi N, Dehghani V, Alavi S A 2019 Nucl. Phys. A 983 77
Google Scholar
[33] Sinha B 1975 Phys. Rep. 20 1
Google Scholar
[34] Satchler G R, Love W G 1979 Phys. Rep. 55 183
Google Scholar
[35] Wang M, Huang W J, Kondev F G, Audi G, Naimi S 2021 Chin. Phys. C 45 030003
Google Scholar
[36] Landau L D, Lifshitz E M 2013 Quantum Mechanics: Non-relativistic Theory (Castellana: Elsevier) p472
[37] Royer G 2010 Nucl. Phys. A 848 279
Google Scholar
[38] Basu D N 2003 Phys. Lett. B 566 90
Google Scholar
[39] Heisenberg W, Euler H 1936 Z. Phys. 98 714
Google Scholar
[40] Sauter F 1931 Z. Phys. 69 742
Google Scholar
[41] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
-
图 1 原子核半衰期数值计算结果及对比
Figure 1. Results and comparison of nuclear half-lives.
图 2 G值(a)和Qα值(b)与激光诱导作用的相关性
Figure 2. Correlation between G (a) and Qα (b) values and laser induction.
图 3 激光功率密度与激光诱导作用的相关性
Figure 3. Correlation between laser power density and laser induction.
表 1 原子核半衰期数值计算结果及对比, 其中核素的实验数据及不同理论方法计算数据分别来自文献[7,19,37,38]
Table 1. Calculation results and comparison of nuclear half-lives. These data are from Refs. [7,19,37,38].
核素 Qα/MeV R/fm $ {T}_{1/2}^{{\mathrm{e}}{\mathrm{x}}} $/s $ {T}_{1/2}^{{\mathrm{c}}{\mathrm{a}}{\mathrm{l}}} $/s $ {T}_{1/2}^{{\mathrm{r}}{\mathrm{e}}{\mathrm{f}}} $/s 文献 n/% $ {}_{60}^{144}{\mathrm{N}}{\mathrm{d}} $ 1.907 7.755 (7.222±0.505)×1022 7.371×1022 5.600×1022 [19] 0.304 $ {}_{62}^{146}{\mathrm{S}}{\mathrm{m}} $ 2.529 7.758 (2.144±0.221)×1015 1.889×1015 2.176×1015 [7] 0.180 $ {}_{64}^{152}{\mathrm{G}}{\mathrm{d}} $ 2.205 7.786 (3.406±0.252)×1021 3.640×1021 6.276×1021 [7] 0.240 $ {}_{68}^{154}{\mathrm{E}}{\mathrm{r}} $ 4.280 7.767 (4.786±0.266)×104 2.294×104 3.890×104 [37] 0.072 $ {}_{70}^{158}{\mathrm{Y}}{\mathrm{b}} $ 4.180 7.790 (4.266±0.517)×106 5.709×106 4.169×105 [38] 0.074 $ {}_{72}^{174}{\mathrm{H}}{\mathrm{f}} $ 2.559 8.161 (6.307±1.261)×1022 4.944×1022 1.397×1023 [7] 0.250 $ {}_{74}^{162}{\mathrm{W}} $ 5.675 7.787 1.390±0.142 2.752 2.450 [19] 0.035 $ {}_{76}^{186}{\mathrm{O}}{\mathrm{s}} $ 2.822 7.887 (6.307±3.469)×1022 7.679×1022 4.226×1022 [7] 0.235 $ {}_{78}^{190}{\mathrm{P}}{\mathrm{t}} $ 3.243 7.895 (2.050±0.095)×1019 2.422×1019 5.248×1018 [37] 0.195 $ {}_{80}^{178}{\mathrm{H}}{\mathrm{g}} $ 6.580 7.820 0.363±0.010 0.416 0.091 [38] 0.034 $ {}_{84}^{212}{\mathrm{P}}{\mathrm{o}} $ 8.953 8.676 (2.990±0.002)×10–7 2.615×10–7 1.600×10–7 [19] 0.052 $ {}_{87}^{219}{\mathrm{F}}{\mathrm{r}} $ 7.460 8.457 (1.995±0.517)×10–2 3.079×10–2 3.020×10–2 [38] 0.072 $ {}_{88}^{220}{\mathrm{R}}{\mathrm{a}} $ 7.600 8.463 (2.512±0.060)×10–2 2.728×10–2 1.660×10–2 [38] 0.066 $ {}_{90}^{222}{\mathrm{T}}{\mathrm{h}} $ 8.133 8.467 (2.818±0.302)×10–3 3.433×10–3 2.188×10–3 [38] 0.062 $ {}_{92}^{238}{\mathrm{U}} $ 4.274 8.918 (1.400±0.175)×1017 3.070×1017 4.300×1017 [19] 0.213 $ {}_{94}^{238}{\mathrm{P}}{\mathrm{u}} $ 5.593 9.196 (2.771±0.003)×109 2.930×109 4.400×109 [19] 0.139 
DownLoad: CSV
-
[1] Gamow G 1928 Z. Phys. 51 204
Google Scholar
[2] Gurney R W, Condon E U 1929 Phys. Rev. 33 127
Google Scholar
[3] Yahya W A, Kimene Kaya B D C 2022 Int. J. Mod. Phys. E 31 2250002
[4] Gontchar I I, Chushnyakova M V 2010 Comput. Phys. Commun. 181 168
Google Scholar
[5] Deng J G, Zhao J C, Chu P C, Li X H 2018 Phys. Rev. C 97 044322
Google Scholar
[6] 邓军刚 2022 博士学位论文 (兰州: 兰州大学)第27—44页
Deng J G 2022 Ph. D. Dissertation (Lanzhou: Lanzhou University) pp27–44
[7] Qian Y, Ren Z 2014 Phys. Lett. B 738 87
Google Scholar
[8] Mourou G 2019 Rev. Mod. Phys. 91 030501
Google Scholar
[9] 沈百飞, 吉亮亮, 张晓梅, 步志刚, 徐建彩 2021 70 084101
Google Scholar
Shen B F, Ji L L, Zhang X M, Bu Z G, Xu J C 2021 Acta Phys. Sin. 70 084101
Google Scholar
[10] Ledingham K W D, Spencer I, McCanny T, Singhal R P, Santala M I K, Clark E, Watts I, Beg F N, Zepf M, Krushelnick K, Tatarakis M, Dangor A E, Norreys P A, Allott R, Neely D, Clark R J, Machacek A C, Wark J S, Cresswell A J, Sanderson D C W, Magill J 2000 Phys. Rev. Lett. 84 899
Google Scholar
[11] 席晓峰, 郭冰, 符长波, 吕冲, 张国强 2023 原子能科学技术 57 865
Google Scholar
Xi X F, Guo B, Fu C B, Lü C, Zhang G Q 2023 At. Energy Sci. Technol. 57 865
Google Scholar
[12] Castañeda Cortés H M 2012 Ph. D. Dissertation (Heidelberg: Ruprecht-Karls-Universität) pp69–103
[13] Buck B, Merchant A C, Perez S M 1990 Phys. Rev. Lett. 65 2975
Google Scholar
[14] Qi J T, Li T, Xu R H, Fu L B, Wang X 2019 Phys. Rev. C 99 044610
Google Scholar
[15] Delion D S, Ghinescu S A 2017 Phys. Rev. Lett. 119 202501
Google Scholar
[16] Wang X 2020 Phys. Rev. C 102 011601
Google Scholar
[17] Qi J 2022 Nucl. Phys. A 1020 122394
Google Scholar
[18] Qi J, Fu L 2020 Phys. Rev. C 102 064629
Google Scholar
[19] Pálffy A, Popruzhenko S V 2020 Phys. Rev. Lett. 124 212505
Google Scholar
[20] Cortés H C, Popruzhenko S V, Bauer D, Pálffy A 2011 New J. Phys. 13 063007
Google Scholar
[21] Queisser F, Schützhold R 2019 Phys. Rev. C 100 041601
[22] Ur C A, Balabanski D, Cata-Danil G, Gales S, Morjan I, Tesileanu O, UrsescuD, Ursu I, Zamfir N V 2015 Nucl. Instrum. Methods Phys. Res., Sect. B 355 198
Google Scholar
[23] Balabanski D L, Constantin P, Rotaru A, State A 2019 Hyperfine Interact. 240 49
Google Scholar
[24] Zhang Z X, Wu F X, Hu J B, Yang X J, Gui J Y, Ji P H, Liu X Y, Wang C, Liu Y Q, Lu X M, Xu Y, Leng Y X, Li R X, Xu Z Z 2020 High Power Laser Sci. Eng. 8 e4
Google Scholar
[25] Li W Q, Gan Z B, Yu L H, Wang C, Liu Y Q, Guo Z, Xu L, Xu M, Hang Y, Xu Y, Wang J Y, Huang P, Cao H, Yao B, Zhang X B, Chen L R, Tang Y H, Li S, Liu X Y, Li S M, He M Z, Yin D J, Liang X Y, Leng Y X, Li R X, Xu Z Z 2018 Opt. Lett. 43 5681
Google Scholar
[26] Buck B, Merchant A C, Perez S M 1991 J. Phys. G: Nucl. Part. Phys. 17 1223
[27] Bertsch G, Borysowicz J, McManus H, Love W G 1977 Nucl. Phys. A 284 399
Google Scholar
[28] Wildermuth K, Kanellopoulos T 1958 Nucl. Phys. 7 150
Google Scholar
[29] 卢希庭 2000 原子核物理 (修订版) (北京: 原子能出版社) 第22页
Lu X T 2000 Nuclear Physics (Rev. Ed.) (Beijing: Atomic Energy Publishing House) p22
[30] Jeffreys H 1925 Proceedings of the London Mathematical Society s2-23 428
Google Scholar
[31] 邢凤竹, 崔建坡, 王艳召, 顾建中 2022 71 062301
Google Scholar
Xing F Z, Cui J P, Wang Y Z, Gu J Z 2022 Acta Phys. Sin. 71 062301
Google Scholar
[32] Maroufi N, Dehghani V, Alavi S A 2019 Nucl. Phys. A 983 77
Google Scholar
[33] Sinha B 1975 Phys. Rep. 20 1
Google Scholar
[34] Satchler G R, Love W G 1979 Phys. Rep. 55 183
Google Scholar
[35] Wang M, Huang W J, Kondev F G, Audi G, Naimi S 2021 Chin. Phys. C 45 030003
Google Scholar
[36] Landau L D, Lifshitz E M 2013 Quantum Mechanics: Non-relativistic Theory (Castellana: Elsevier) p472
[37] Royer G 2010 Nucl. Phys. A 848 279
Google Scholar
[38] Basu D N 2003 Phys. Lett. B 566 90
Google Scholar
[39] Heisenberg W, Euler H 1936 Z. Phys. 98 714
Google Scholar
[40] Sauter F 1931 Z. Phys. 69 742
Google Scholar
[41] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2351
- PDF Downloads: 68
- Cited By: 0
