-
The transportable quantum memory is a feasible solution for realizing the long-distance quantum communication, which requires a storage lifetime of the order of hours. The isotope-enriched 151Eu3+:Y2SiO5 crystal is a promising candidate for this application. However, its optical storage efficiency and spin storage lifetime are limited by the wide inhomogeneous linewidth. In this work, we successfully grow isotope-enriched 151Eu3+:Y2SiO5 crystals with varying doping concentrations by utilizing the Czochralski method. The optical inhomogeneous broadening and spin inhomogeneous broadening are measured by the optical absorption spectroscopy and optically detected magnetic resonance tests, respectively. Notably, in the undoped samples, we identify a baseline level of inhomogeneous linewidths, happening at (390 ± 15) MHz for optical inhomogeneous broadening and (4.6 ± 0.2) kHz for spin inhomogeneous broadening. Our findings reveal that the point defects, induced by the doping ions, significantly contribute to the inhomogeneous broadening. For every increase of 10–6 in doping concentration, the optical inhomogeneous broadening increases by 0.97 MHz, and the spin inhomogeneous broadening increases by 0.014 kHz. Furthermore, we discuss the influence of dislocations on inhomogeneous broadening and propose potential strategies to further mitigate these effects. These advancements are expected to promote the development of ultra-long-lifetime transportable quantum memory applications.
-
Keywords:
- rare-earth-doped crystal /
- quantum memory /
- optical inhomogeneous broadening /
- spin inhomogeneous broadening
[1] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221
Google Scholar
[2] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[3] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[4] Zhong M, Hedges M P, Ahlefeldt R L, Bartholomew J G, Beavan S E, Wittig S M, Longdell J J, Sellars M J 2015 Nature 517 177
Google Scholar
[5] Ma Y, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 2381
Google Scholar
[6] Yin J, Cao Y, Li Y H, Liao S K, Zhang L, Ren J G, Cai W Q, Liu W Y, Li B, Dai H, Li G B, Lu Q M, Gong Y H, Xu Y, Li S L, Li F Z, Yin Y Y, Jiang Z Q, Li M, Jia J J, Ren G, He D, Zhou Y L, Zhang X X, Wang N, Chang X, Zhu Z C, Liu N L, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Science 356 1140
Google Scholar
[7] Lukin M D 2003 Rev. Mod. Phys. 75 457
Google Scholar
[8] Moehring D L, Maunz P, Olmschenk S, Younge K C, Matsukevich D N, Duan L M, Monroe C 2007 Nature 449 68
Google Scholar
[9] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
Google Scholar
[10] Ritter S, Nölleke C, Hahn C, Reiserer A, Neuzner A, Uphoff M, Mücke M, Figueroa E, Bochmann J, Rempe G 2012 Nature 484 195
Google Scholar
[11] van Leent T, Bock M, Fertig F, Garthoff R, Eppelt S, Zhou Y, Malik P, Seubert M, Bauer T, Rosenfeld W, Zhang W, Becher C, Weinfurter H 2022 Nature 607 69
Google Scholar
[12] Pompili M, Hermans S L N, Baier S, Beukers H K C, Humphreys P C, Schouten R N, Vermeulen R F L, Tiggelman M J, dos Santos Martins L, Dirkse B, Wehner S, Hanson R 2021 Science 372 259
Google Scholar
[13] Eisaman M D, André A, Massou F, Fleischhauer M, Zibrov A S, Lukin M D 2005 Nature 438 837
Google Scholar
[14] Choi K S, Deng H, Laurat J, Kimble H J 2008 Nature 452 67
Google Scholar
[15] Vernaz-Gris P, Huang K, Cao M, Sheremet A S, Laurat J 2018 Nat. Commun. 9 363
Google Scholar
[16] Wang Y, Li J, Zhang S, Su K, Zhou Y, Liao K, Du S, Yan H, Zhu S L 2019 Nat. Photonics 13 346
Google Scholar
[17] Yu Y, Ma F, Luo X Y, Jing B, Sun P F, Fang R Z, Yang C W, Liu H, Zheng M Y, Xie X P, Zhang W J, You L X, Wang Z, Chen T Y, Zhang Q, Bao X H, Pan J W 2020 Nature 578 240
Google Scholar
[18] Julsgaard B, Sherson J, Cirac J I, Fiurášek J, Polzik E S 2004 Nature 432 482
Google Scholar
[19] Hosseini M, Sparkes B M, Campbell G, Lam P K, Buchler B C 2011 Nat. Commun. 2 174
Google Scholar
[20] Chrapkiewicz R, Dąbrowski M, Wasilewski W 2017 Phys. Rev. Lett. 118 063603
Google Scholar
[21] Li H, Dou J P, Pang X L, Yang T H, Zhang C N, Chen Y, Li J M, Walmsley I A, Jin X M 2021 Optica 8 925
Google Scholar
[22] Ma L, Lei X, Yan J, Li R, Chai T, Yan Z, Jia X, Xie C, Peng K 2022 Nat. Commun. 13 2368
Google Scholar
[23] de Riedmatten H, Afzelius M, Staudt M U, Simon C, Gisin N 2008 Nature 456 773
Google Scholar
[24] Hedges M P, Longdell J J, Li Y, Sellars M J 2010 Nature 465 1052
Google Scholar
[25] Zhou Z Q, Lin W B, Yang M, Li C F, Guo G C 2012 Phys. Rev. Lett. 108 190505
Google Scholar
[26] Sabooni M, Li Q, Kröll S, Rippe L 2013 Phys. Rev. Lett. 110 133604
Google Scholar
[27] Tang J S, Zhou Z Q, Wang Y T, Li Y L, Liu X, Hua Y L, Zou Y, Wang S, He D Y, Chen G, SunY N, Yu Y, Li M F, Zha G W, Ni H Q, Niu Z C, Li C F, Guo G C 2015 Nat. Commun. 6 8652
Google Scholar
[28] Yang T S, Zhou Z Q, Hua Y L, Liu X, Li Z F, Li P Y, Ma Y, Liu C, Liang P J, Li X, Xiao Y X, Hu J, Li C F, Guo G C 2018 Nat. Commun. 9 3407
Google Scholar
[29] Lago-Rivera D, Grandi S, Rakonjac J V, Seri A, de Riedmatten H 2021 Nature 594 37
Google Scholar
[30] Ortu A, Holzäpfel A, Etesse J, Afzelius M 2022 npj Quantum Inf. 8 29
Google Scholar
[31] Ma Y Z, Jin M, Chen D L, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 4378
Google Scholar
[32] Liu X, Hu J, Li Z F, Li X, Li P Y, Liang P J, Zhou Z Q, Li C F, Guo G C 2021 Nature 594 41
Google Scholar
[33] Stuart J S, Hedges M, Ahlefeldt R, Sellars M 2021 Phys. Rev. Res. 3 L032054
Google Scholar
[34] Askarani M F, Das A, Davidson J H, Amaral G C, Sinclair N, Slater J A, Marzban S, Thiel C W, Cone R L, Oblak D, Tittel W 2021 Phys. Rev. Lett. 127 220502
Google Scholar
[35] Businger M, Tiranov A, Kaczmarek K T, Welinski S, Zhang Z, Ferrier A, Goldner P, Afzelius M 2020 Phys. Rev. Lett. 124 053606
Google Scholar
[36] Liu D C, Li P Y, Zhu T X, Zheng L, Huang J Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 129 210501
Google Scholar
[37] Liu C, Zhu T X, Su M X, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 260504
Google Scholar
[38] Zhu T X, Liu C, Jin M, Su M X, Liu Y P, Li W J, Ye Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 128 180501
Google Scholar
[39] Equall R W, Sun Y, Cone R L, Macfarlane R M 1994 Phys. Rev. Lett. 72 2179
Google Scholar
[40] Könz F, Sun Y, Thiel C W, Cone R L, Equall R W, Hutcheson R L, Macfarlane R M 2003 Phys. Rev. B 68 085109
Google Scholar
[41] Ma Y Z, Lv Y C, Yang T S, Ma Y, Zhou Z Q, Li C F, Guo G C 2023 Phys. Rev. B 107 014310
Google Scholar
[42] Stoneham A M 1969 Rev. Mod. Phys. 41 82
Google Scholar
[43] Ching W Y, Ouyang L, Xu Y N 2003 Phys. Rev. B 67 245108
Google Scholar
[44] Thorpe M J, Leibrandt D R, Rosenband T 2013 New J. Phys. 15 033006
Google Scholar
[45] Lauritzen B, Timoney N, Gisin N, Afzelius M, de Riedmatten H, Sun Y, Macfarlane R M, Cone R L 2012 Phys. Rev. B 85 115111
Google Scholar
[46] Lafitte-Houssat E, Ferrier A, Welinski S, Morvan L, Afzelius M, Berger P, Goldner P 2022 Opt. Mater. X 14 100153
Google Scholar
[47] Cardona M 2001 Solid State Commun. 121 7
Google Scholar
[48] Macfarlane R M, Cassanho A, Meltzer R S 1992 Phys. Rev. Lett. 69 542
Google Scholar
[49] Holt D B, Yacobi B G 2007 Characterization of Extended Defects in Semiconductors (Cambridge University Press) pp122–162
[50] Oda O 2001 Encyclopedia of Materials: Science and Technology (Oxford: Elsevier) pp8374–8379
[51] 周宗权 2022 71 070305
Google Scholar
Zhou Z Q 2022 Acta Phys. Sin. 71 070305
Google Scholar
-
图 1 (a) Y2SiO5中替位1处的$ {{^{151}{\rm{Eu}}^{3+}}} $在磁场为0时7F0$ \rightarrow $5D0跃迁能级图. f0 = 516.8472 THz, f1 = f0 + 34.5 MHz, f2 = f0 – 20.9 MHz. (b)测试$ { |{\pm1/2}\rangle_{\mathrm{g}}\rightarrow|{\pm3/2}\rangle_{\mathrm{g}}} $自旋跃迁谱的脉冲时序. 准备阶段包括类清理和自旋极化过程, 脉冲频率与图(a)中的相同颜色箭头对应, 准备阶段所有脉冲都是时间宽度为1 ms, 扫频宽度为4 MHz的啁啾脉冲. 在准备阶段结束10 ms之后, 线圈产生一个时间宽度为1 ms的RF高斯脉冲. RF脉冲结束10 µs后, 一个啁啾型泵浦光脉冲被施加到样品上, 其时间宽度为1 ms, 扫频宽度为3.8 MHz. 泵浦光脉冲结束10 µs后, 光开关门被打开, 为单光子探测器提供一个2 ms的探测时间窗口. (c) Y2SiO5晶碇, 样品取自蓝框区域的晶体中心位置
Fig. 1. (a) Level structure of 7F0$ \rightarrow $5D0 transition for the $ {{^{151}{\rm{Eu}}^{3+}}} $ at site 1 in the Y2SiO5 under a zero magnetic field. f0 = 516.8472 THz, f1 = f0 + 34.5 MHz, f2 = f0 – 20.9 MHz. (b) Pulse sequence measuring the spin transition $ {|{\pm1/2}\rangle_{\mathrm{g}}\rightarrow|{\pm3/2}\rangle_{\mathrm{g}} } $. The preparation includes the process of class cleaning and polarization. The frequency of these pulses is corresponding to the frequency of the arrows of the same color in Fig (a). Every pulse during the preparation is a chirp pulse with a duration of 1 ms and a bandwidth of 4 MHz. A Gaussian pulse, with a duration of 1 ms, is generated by the Coil 10 ms later after the end of preparation. A chirp pulse, with a duration of 1 ms and a bandwidth of 3.8 MHz, is applied to the sample 10 µs later after the RF pulses. The gate is turned on, 10 µs later after the pumping pulse, to provide a 2 ms detection window for the single photon detector. (c) Y2SiO5 boule, and the sample is taken from the center of the crystal in the blue rectangular area.
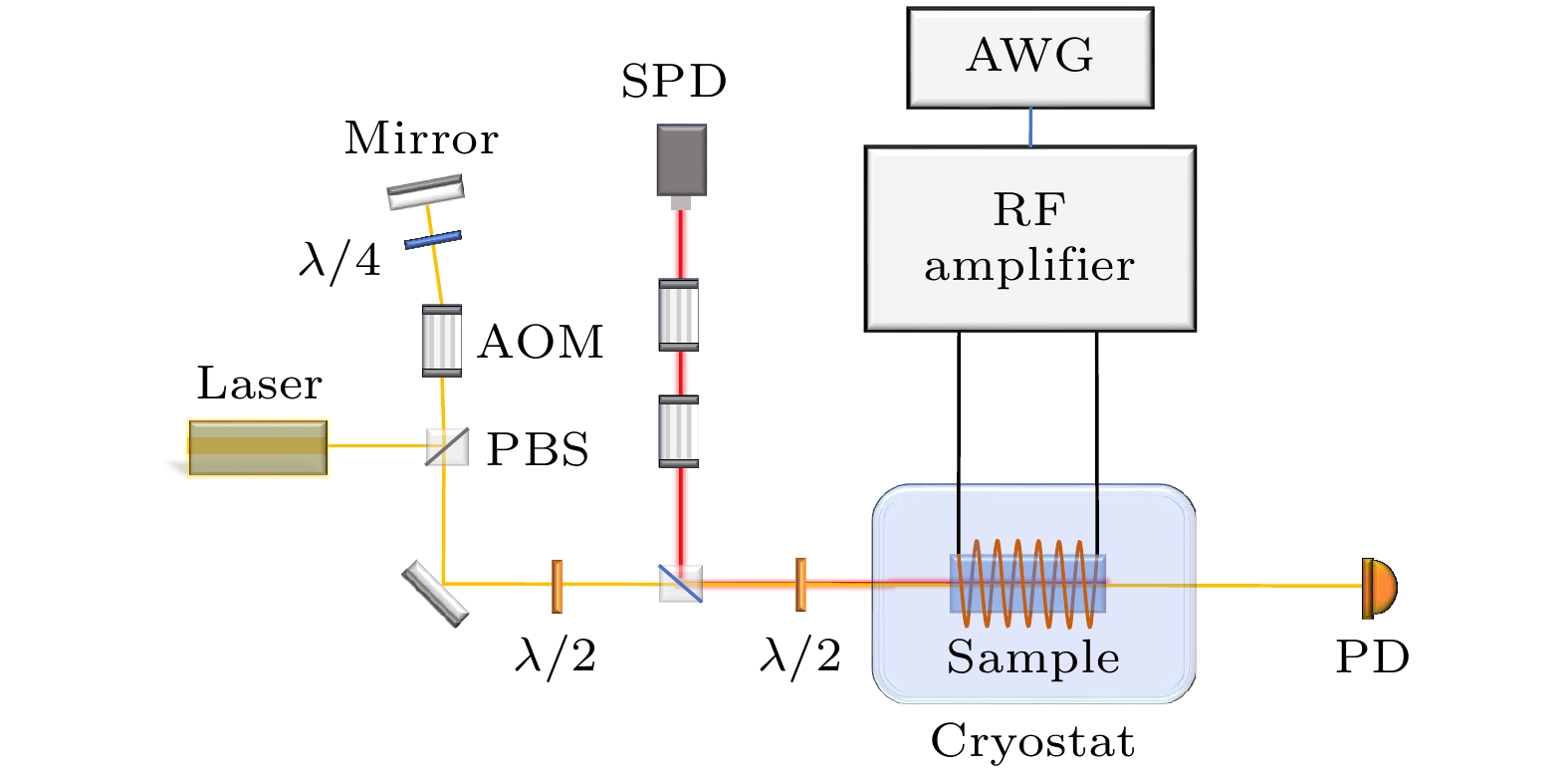
图 2 实验装置图. 580 nm激光(黄线)经过双次通过声光调制器(AOM)调制, 以控制其频率和强度. 调制后的激光脉冲通过低温恒温腔中的样品. 透过样品的激光通过光电探测器(PD)探测, 用于获得光学吸收谱. 同时, 样品在激光激发下的荧光(红线)经过偏振分束器(PBS)偏振滤波. 反向收集的荧光, 通过由两个声光调制器组成的光开关门, 进入单光子探测器(SPD). 线圈的激励射频信号由AWG产生, 并经射频放大器放大
Fig. 2. Diagram of experiment set-up. The 580 nm laser (yellow line) is modulated by a double-pass acousto-optic modulator (AOM) to control its frequency and intensity. The modulated laser pulse passes through the sample in a cryostat. The laser passing through the sample is detected by a photo detector (PD) to measure the absorption spectrum. At the same time, the fluorescence (red line) of the sample excited by the laser is filtered by a polarizing beam splitter (PBS). The fluorescence collected in the reverse direction enters a single-photon detector (SPD) through a gate consisting of two acousto-optic modulators. The radio-frequency excitation signal is generated by an AWG and amplified by a radio frequency amplifier.
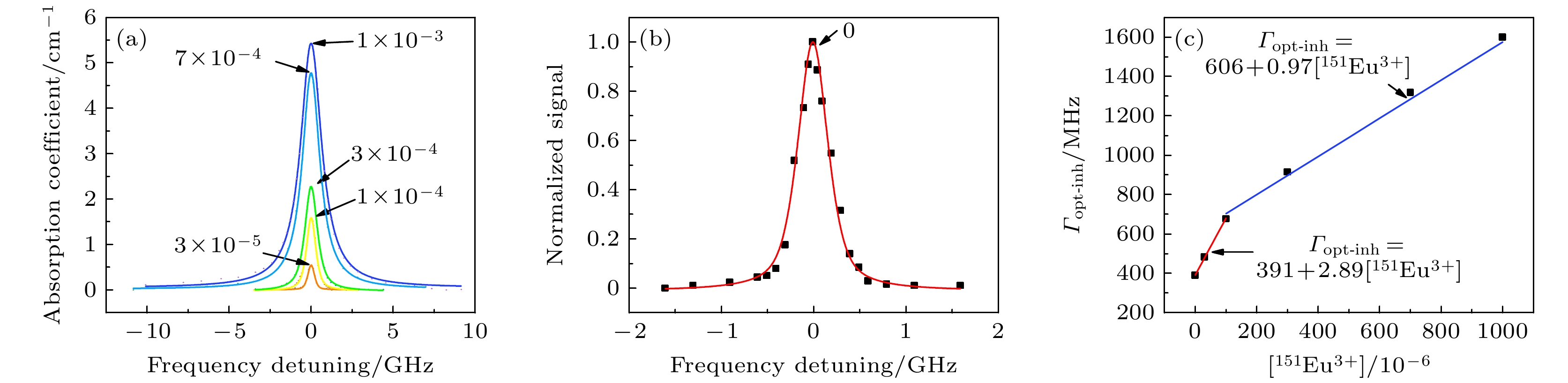
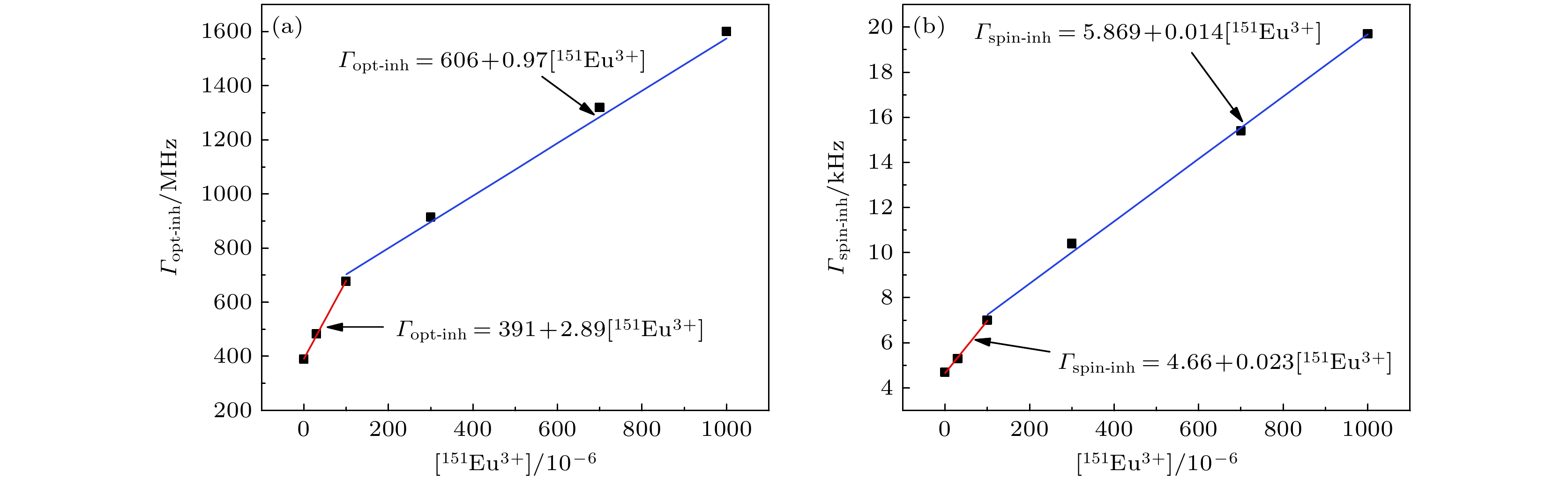
图 3 (a) Y2SiO5中替位1处不同掺杂浓度下Eu3+离子7F0$ \rightarrow $5D0跃迁光学吸收谱. (b) 零掺杂样品的7F0$ \rightarrow $5D0跃迁荧光激发谱, 黑色方块为数据点, 红色曲线是拟合曲线. (c) 151Eu3+:Y2SiO5光学非均匀展宽与掺杂浓度拟合图. $ [^{151} {\rm{Eu}} ^{3+}] $表示151Eu3+掺杂浓度. $ \varGamma_\text{{\rm{opt}}-{\rm{inh}}} $表示光学非均匀展宽. 黑色方块为数据点, 红色线和蓝色线分别是0—10–4和10–4—10–3的线性拟合. 拟合方程展示在图中, 并由箭头指向各自曲线
Fig. 3. (a) Optical absorption spectrum for the 7F0$ \rightarrow $5D0 transition of Eu3+ ions at site 1 in Y2SiO5 with variable doping concentrations. (b) Fluorescence excitation spectrum for the 7F0$ \rightarrow $5D0 transition of the 0 ppm sample, and the black squares represent the data points, red curve is the fitting curve. (c) Optical inhomogeneous linewidth fitted as a function of 151Eu3+ concentrations. $ [^{151} {\rm{Eu}} ^{3+}]$ is the concentration of 151Eu3+ ions. $ \varGamma_\text{{\rm{opt}}-{\rm{inh}}} $ is the optical inhomogeneous linewidth. Black squares stand for the data points. Red and blue lines represent linear fits of 0–10–4 and 10–4–10–3, respectively. The fitting equations are depicted in the graph, accompanied by arrows indicating their corresponding lines.
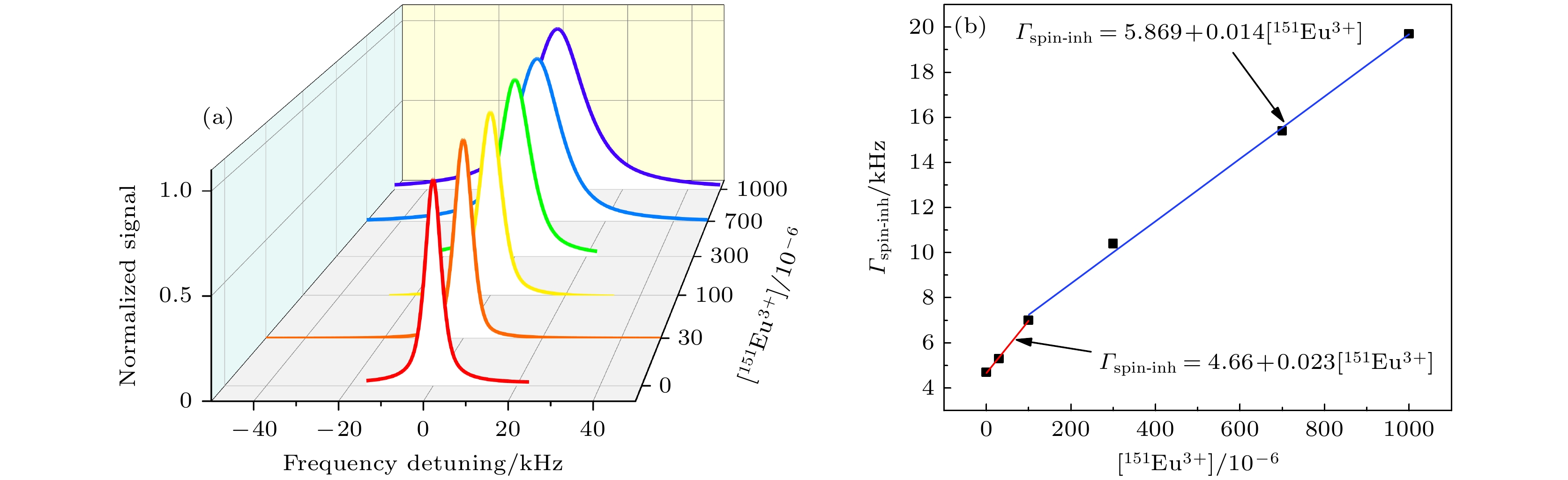
图 4 (a) Y2SiO5中不同掺杂浓度下151Eu3+离子基态$ { |{\pm1/2}\rangle_{\rm{g}}\rightarrow|{\pm3/2}\rangle_{\rm{g}}} $自旋跃迁谱. (b)自旋非均匀展宽随浓度变化的拟合曲线. $ [^{151} {\rm{Eu}} ^{3+}] $表示151Eu3+掺杂浓度. $ \varGamma_{\text{spin-inh}} $表示自旋非均匀展宽. 黑色方块是数据点, 红色和蓝色线分别是从0—10–4和10–4—10–3的线性拟合曲线. 图中各曲线给出了对应的拟合方程
Fig. 4. (a) Spin transition spectrum for the ground-state $ { |{\pm1/2}\rangle_{\rm{g}}\rightarrow|{\pm3/2}\rangle_{\rm{g}}} $ transition of 151Eu3+ ions in Y2SiO5 with variable doping concentrations. (b) Fitting curve of concentration-dependent variation in the spin inhomogeneous broadening. $ [^{151} {\rm{Eu}} ^{3+}] $ stands for the concentration of 151Eu3+ ions. $ \varGamma_{\text{spin-inh}} $ represents the spin inhomogeneous linewidth. Black squares are the data points, and the red and blue lines represent linear fits ranging from 0–10–4 and from 10–4–10–3, respectively. Fitted equations are illustrated for their respective lines in the graph.
表 1 Y2SiO5中同位素提纯151Eu3+中不同掺杂浓度下拟合结果参数表. $ [^{151} {\rm{Eu}} ^{3+}] $表示151Eu3+掺杂浓度, $ \varGamma_{ {\rm{opt}}\text-{\rm{inh}}} $表示光学非均匀展宽, $ \varGamma_{\text{spin-inh}} $表示自旋非均匀展宽, µ1和µ2分别表示光学吸收谱和自旋跃迁谱pseudo-Voigt拟合洛伦兹部分的权重
Table 1. Parameter table of the fitting results for variable doping concentrations of isotope-enriched 151Eu3+ ions in the Y2SiO5. $ \varGamma_{ \text{opt-inh}} $ represents the optical inhomogeneous linewidth. $ \varGamma_{\text{spin-inh}} $ stands for the spin inhomogeneous linewidth. The weights µ1 and µ2 represent the contributions of the Lorentzian component in the pseudo-Voigt fitting, corresponding to the optical absorption and spin transition, respectively.
$ [^{151} {\rm{Eu}} ^{3+}] $/10–6 $ \varGamma_{\text{\rm opt-inh}}$/MHz $ \varGamma_{\text{spin-inh}} $/kHz µ1 µ2 0 392 ± 15 4.6 ± 0.2 0.65 ± 0.18 0.69 ± 0.15 30 483 ± 15 5.3 ± 0.2 0.54 ± 0.13 0.47 ± 0.14 100 677 ± 8 7.0 ± 0.3 0.74 ± 0.04 0.64 ± 0.16 300 915 ± 9 10.4 ± 0.3 0.83 ± 0.03 0.74 ± 0.12 700 1319 ± 24 15.4 ± 0.4 1 ± 0.05 0.89 ± 0.09 1000 1561 ± 21 19.7 ± 0.2 1 ± 0.03 0.89 ± 0.03 
下载: 导出CSV
-
[1] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221
Google Scholar
[2] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[3] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[4] Zhong M, Hedges M P, Ahlefeldt R L, Bartholomew J G, Beavan S E, Wittig S M, Longdell J J, Sellars M J 2015 Nature 517 177
Google Scholar
[5] Ma Y, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 2381
Google Scholar
[6] Yin J, Cao Y, Li Y H, Liao S K, Zhang L, Ren J G, Cai W Q, Liu W Y, Li B, Dai H, Li G B, Lu Q M, Gong Y H, Xu Y, Li S L, Li F Z, Yin Y Y, Jiang Z Q, Li M, Jia J J, Ren G, He D, Zhou Y L, Zhang X X, Wang N, Chang X, Zhu Z C, Liu N L, Chen Y A, Lu C Y, Shu R, Peng C Z, Wang J Y, Pan J W 2017 Science 356 1140
Google Scholar
[7] Lukin M D 2003 Rev. Mod. Phys. 75 457
Google Scholar
[8] Moehring D L, Maunz P, Olmschenk S, Younge K C, Matsukevich D N, Duan L M, Monroe C 2007 Nature 449 68
Google Scholar
[9] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
Google Scholar
[10] Ritter S, Nölleke C, Hahn C, Reiserer A, Neuzner A, Uphoff M, Mücke M, Figueroa E, Bochmann J, Rempe G 2012 Nature 484 195
Google Scholar
[11] van Leent T, Bock M, Fertig F, Garthoff R, Eppelt S, Zhou Y, Malik P, Seubert M, Bauer T, Rosenfeld W, Zhang W, Becher C, Weinfurter H 2022 Nature 607 69
Google Scholar
[12] Pompili M, Hermans S L N, Baier S, Beukers H K C, Humphreys P C, Schouten R N, Vermeulen R F L, Tiggelman M J, dos Santos Martins L, Dirkse B, Wehner S, Hanson R 2021 Science 372 259
Google Scholar
[13] Eisaman M D, André A, Massou F, Fleischhauer M, Zibrov A S, Lukin M D 2005 Nature 438 837
Google Scholar
[14] Choi K S, Deng H, Laurat J, Kimble H J 2008 Nature 452 67
Google Scholar
[15] Vernaz-Gris P, Huang K, Cao M, Sheremet A S, Laurat J 2018 Nat. Commun. 9 363
Google Scholar
[16] Wang Y, Li J, Zhang S, Su K, Zhou Y, Liao K, Du S, Yan H, Zhu S L 2019 Nat. Photonics 13 346
Google Scholar
[17] Yu Y, Ma F, Luo X Y, Jing B, Sun P F, Fang R Z, Yang C W, Liu H, Zheng M Y, Xie X P, Zhang W J, You L X, Wang Z, Chen T Y, Zhang Q, Bao X H, Pan J W 2020 Nature 578 240
Google Scholar
[18] Julsgaard B, Sherson J, Cirac J I, Fiurášek J, Polzik E S 2004 Nature 432 482
Google Scholar
[19] Hosseini M, Sparkes B M, Campbell G, Lam P K, Buchler B C 2011 Nat. Commun. 2 174
Google Scholar
[20] Chrapkiewicz R, Dąbrowski M, Wasilewski W 2017 Phys. Rev. Lett. 118 063603
Google Scholar
[21] Li H, Dou J P, Pang X L, Yang T H, Zhang C N, Chen Y, Li J M, Walmsley I A, Jin X M 2021 Optica 8 925
Google Scholar
[22] Ma L, Lei X, Yan J, Li R, Chai T, Yan Z, Jia X, Xie C, Peng K 2022 Nat. Commun. 13 2368
Google Scholar
[23] de Riedmatten H, Afzelius M, Staudt M U, Simon C, Gisin N 2008 Nature 456 773
Google Scholar
[24] Hedges M P, Longdell J J, Li Y, Sellars M J 2010 Nature 465 1052
Google Scholar
[25] Zhou Z Q, Lin W B, Yang M, Li C F, Guo G C 2012 Phys. Rev. Lett. 108 190505
Google Scholar
[26] Sabooni M, Li Q, Kröll S, Rippe L 2013 Phys. Rev. Lett. 110 133604
Google Scholar
[27] Tang J S, Zhou Z Q, Wang Y T, Li Y L, Liu X, Hua Y L, Zou Y, Wang S, He D Y, Chen G, SunY N, Yu Y, Li M F, Zha G W, Ni H Q, Niu Z C, Li C F, Guo G C 2015 Nat. Commun. 6 8652
Google Scholar
[28] Yang T S, Zhou Z Q, Hua Y L, Liu X, Li Z F, Li P Y, Ma Y, Liu C, Liang P J, Li X, Xiao Y X, Hu J, Li C F, Guo G C 2018 Nat. Commun. 9 3407
Google Scholar
[29] Lago-Rivera D, Grandi S, Rakonjac J V, Seri A, de Riedmatten H 2021 Nature 594 37
Google Scholar
[30] Ortu A, Holzäpfel A, Etesse J, Afzelius M 2022 npj Quantum Inf. 8 29
Google Scholar
[31] Ma Y Z, Jin M, Chen D L, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 4378
Google Scholar
[32] Liu X, Hu J, Li Z F, Li X, Li P Y, Liang P J, Zhou Z Q, Li C F, Guo G C 2021 Nature 594 41
Google Scholar
[33] Stuart J S, Hedges M, Ahlefeldt R, Sellars M 2021 Phys. Rev. Res. 3 L032054
Google Scholar
[34] Askarani M F, Das A, Davidson J H, Amaral G C, Sinclair N, Slater J A, Marzban S, Thiel C W, Cone R L, Oblak D, Tittel W 2021 Phys. Rev. Lett. 127 220502
Google Scholar
[35] Businger M, Tiranov A, Kaczmarek K T, Welinski S, Zhang Z, Ferrier A, Goldner P, Afzelius M 2020 Phys. Rev. Lett. 124 053606
Google Scholar
[36] Liu D C, Li P Y, Zhu T X, Zheng L, Huang J Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 129 210501
Google Scholar
[37] Liu C, Zhu T X, Su M X, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 260504
Google Scholar
[38] Zhu T X, Liu C, Jin M, Su M X, Liu Y P, Li W J, Ye Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 128 180501
Google Scholar
[39] Equall R W, Sun Y, Cone R L, Macfarlane R M 1994 Phys. Rev. Lett. 72 2179
Google Scholar
[40] Könz F, Sun Y, Thiel C W, Cone R L, Equall R W, Hutcheson R L, Macfarlane R M 2003 Phys. Rev. B 68 085109
Google Scholar
[41] Ma Y Z, Lv Y C, Yang T S, Ma Y, Zhou Z Q, Li C F, Guo G C 2023 Phys. Rev. B 107 014310
Google Scholar
[42] Stoneham A M 1969 Rev. Mod. Phys. 41 82
Google Scholar
[43] Ching W Y, Ouyang L, Xu Y N 2003 Phys. Rev. B 67 245108
Google Scholar
[44] Thorpe M J, Leibrandt D R, Rosenband T 2013 New J. Phys. 15 033006
Google Scholar
[45] Lauritzen B, Timoney N, Gisin N, Afzelius M, de Riedmatten H, Sun Y, Macfarlane R M, Cone R L 2012 Phys. Rev. B 85 115111
Google Scholar
[46] Lafitte-Houssat E, Ferrier A, Welinski S, Morvan L, Afzelius M, Berger P, Goldner P 2022 Opt. Mater. X 14 100153
Google Scholar
[47] Cardona M 2001 Solid State Commun. 121 7
Google Scholar
[48] Macfarlane R M, Cassanho A, Meltzer R S 1992 Phys. Rev. Lett. 69 542
Google Scholar
[49] Holt D B, Yacobi B G 2007 Characterization of Extended Defects in Semiconductors (Cambridge University Press) pp122–162
[50] Oda O 2001 Encyclopedia of Materials: Science and Technology (Oxford: Elsevier) pp8374–8379
[51] 周宗权 2022 71 070305
Google Scholar
Zhou Z Q 2022 Acta Phys. Sin. 71 070305
Google Scholar
下载:
计量
- 文章访问数: 1892
- PDF下载量: 67
- 被引次数: 0
