间接驱动相关条件下的大空间尺度对流受激拉曼侧向散射

曾嘉乐; 练昌旺; 季雨; 闫锐

doi:10.7498/aps.73.20240045

摘要

利用基于光线追踪和对流放大模型的模拟程序PHANTAM, 对神光III原型装置间接驱动相关条件下的大空间尺度受激拉曼散射进行了研究. 模拟结果表明, 在该参数条件下, 真空腔和充气腔中均会发生较强的对流受激拉曼侧向散射过程. 入射光的焦斑大小是影响对流受激拉曼侧向散射的关键因素: 在光强保持不变的条件下, 真空腔和充气腔中受激拉曼侧向散射的对流增益会随焦斑增大而增大, 而在功率保持不变的条件下, 会随焦斑增大而减小. 因此改变焦斑尺寸是调控受激拉曼侧向散射对流增益的有效途径.

关键词:

Abstract

The large-spatial-scale stimulated Raman scattering relevant to the SG-III prototype indirect drive parameters is investigated by using the code PHANTAM, which is based on ray tracing and convective amplification. The simulations show that strong stimulated Raman side scattering processes occur in both empty hohlraum and gasfilled hohlraum. The incident laser spot size is found to be the critical factor affecting stimulated Raman side scattering: under the constant laser intensity conditions, the convective gain of stimulated Raman side scattering increases with the laser spot size increasing in both types of hohlraums. In our simulations, the wavenumber mismatch leads to a saturation of the convection gain of the stimulated Raman side scattering in empty hohlraum, while in gas-filled hohlraum the convection gain of the stimulated Raman side scattering keeps increasing as the spot size increases. Under constant laser power conditions, the convective gain of stimulated Raman side scattering decreases while laser spot size increases, and the convective gain of stimulated Raman side scattering decreases faster in empty hohlraum in our simulations. The convective gain of Raman side scattering can be adjusted by laser spot size.

Keywords:

作者及机构信息

1.
中国科学技术大学近代力学系, 合肥　230026

2.
上海交通大学IFSA协同创新中心, 上海　200240

通信作者: 练昌旺, lcw1993@ustc.edu.cn ; 闫锐, ruiyan@ustc.edu.cn

基金项目: 国家自然科学基金(批准号: 12375243, 12388101)、中国科学院战略性先导科技专项(批准号: XDA25050400)和挑战计划项目资助的课题.

Authors and contacts

1.
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China

2.
Collaborative Innovation Center for IFSA, Shanghai Jiao Tong University, Shanghai 200240, China

Corresponding author: Lian Chang-Wang, lcw1993@ustc.edu.cn ; Yan Rui, ruiyan@ustc.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12375243, 12388101), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA25050400), and the Science Challenge Project.

文章全文 : translate this paragraph

参考文献

[1]	Betti R, Hurricane O A 2016 Nat. Phys. 12 435 Google Scholar
[2]	Craxton R S, Anderson K S, Boehly T R, et al. 2015 Phys. Plasmas 22 110501 Google Scholar
[3]	Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339 Google Scholar
[4]	Zylstra A B, Hurricane O A, Callahan D A, et al. 2022 Nature 601 542 Google Scholar
[5]	Abu-Shawareb H, Acree R, Adams P, et al. 2022 Phys. Rev. Lett. 129 075001 Google Scholar
[6]	Betti R 2022 Nat. Rev. Phys. 5 6 Google Scholar
[7]	Tollefson J, Gibney E 2022 Nature 612 597 Google Scholar
[8]	Hayes A C, Kyrala G, Gooden M, et al. 2023 Phys. Plasmas 30 072704 Google Scholar
[9]	Kruer W L 1988 The Physics of Laser Plasma Interactions (New York: Addison-Wesley) pp73–85
[10]	Strozzi D J, Bailey D S, Michel P, Divol L, Sepke S M, Kerbel G D, Thomas C A, Ralph J E, Moody J D, Schneider M B 2017 Phys. Rev. Lett. 118 025002 Google Scholar
[11]	Montgomery D S 2016 Phys. Plasmas 23 055601 Google Scholar
[12]	Rosenberg M J, Solodov A A, Seka W, et al. 2020 Phys. Plasmas 27 042705 Google Scholar
[13]	Yan R, Li J, Ren C 2014 Phys. Plasmas 21 062705 Google Scholar
[14]	Liu C S, Rosenbluth M N, White R B 1973 Phys. Rev. Lett. 31 697 Google Scholar
[15]	Afeyan B B, Williams E A 1985 Phys. Fluids 28 3397 Google Scholar
[16]	Figueroa H, Joshi C, Azechi H, Ebrahim N A, Estabrook K 1984 Phys. Fluids 27 1887 Google Scholar
[17]	Drake R P, Turner R E, Lasinski B F, Estabrook K G, Campbell E M, Wang C L, Phillion D W, Williams E A, Kruer W L 1984 Phys. Rev. Lett. 53 1739 Google Scholar
[18]	Drake R P, Turner R E, Lasinski B F, et al. 1988 Phys. Fluids 31 3130 Google Scholar
[19]	Renard N, Labaune C, Baldis H A, Bauer B S, Quesnel B, Schifano E, Michard A, Seka W, Estabrook K G 1996 Phys. Rev. Lett. 77 3807 Google Scholar
[20]	Michel P, Rosenberg M J, Seka W, et al. 2019 Phys. Rev. E 99 033203 Google Scholar
[21]	Rosenberg M J, Solodov A A, Myatt J F, et al. 2023 Phys. Plasmas 30 042710 Google Scholar
[22]	Depierreux S, Neuville C, Baccou C, et al. 2016 Phys. Rev. Lett. 117 235002 Google Scholar
[23]	Hironaka S, Sivajeyan J, Wang J, Rosenberg M J, Solodov A, Filkins T, Xiao C, Wang Q, Seka W, Myatt J F 2023 Phys. Plasmas 30 022708 Google Scholar
[24]	Short R W 2020 Phys. Plasmas 27 042703 Google Scholar
[25]	Michel P, Divol L, Dewald E L, Milovich J L, Hohenberger M, Jones O S, Hopkins L B, Berger R L, Kruer W L, Moody J D 2015 Phys. Rev. Lett. 115 055003 Google Scholar
[26]	Dewald E L, Hartemann F, Michel P, et al. 2016 Phys. Rev. Lett. 116 075003 Google Scholar
[27]	Moody J D, Datte P, Krauter K, et al. 2010 Rev. Sci. Instrum 81 10D921 Google Scholar
[28]	Hall G N, Jones O S, Strozzi D J, et al. 2017 Phys. Plasmas 24 052706 Google Scholar
[29]	Hao L, Zhao Y, Yang D, et al. 2014 Phys. Plasmas 21 072705 Google Scholar
[30]	Strozzi D J, Williams E A, Hinkel D E, Froula D H, London R A, Callahan D A 2008 Phys. Plasmas 15 102703 Google Scholar
[31]	龚韬 2015 博士学位论文 (合肥: 中国科学技术大学) Gong T 2015 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[32]	Xiao C Z, Wang Q, Myatt J F 2023 Phys. Rev. E 107 025203 Google Scholar
[33]	Hao L, Yang D, Li X, et al. 2019 AIP Adv. 9 095201 Google Scholar
[34]	Colaïtis A, Igumenshchev I, Mathiaud J, Goncharov V 2021 J. Comput. Phys. 443 110537 Google Scholar
[35]	Debayle A, Ruyer C, Morice O, Masson-Laborde P E, Loiseau P, Benisti D 2019 Phys. Plasmas 26 092705 Google Scholar
[36]	Colaïtis A, Follett R K, Palastro J P, Igumenschev I, Goncharov V 2019 Phys. Plasmas 26 072706 Google Scholar
[37]	Follett R K, Edgell D H, Froula D H, Goncharov V N, Igumenshchev I V, Shaw J G, Myatt J F 2017 Phys. Plasmas 24 103128 Google Scholar
[38]	Kaiser T B 2000 Phys. Rev. E 61 895 Google Scholar
[39]	Forslund D W, Kindel J M, Lindman E L 1975 Physics of Fluids 18 1002 Google Scholar
[40]	Drake J F, Kaw P K, Lee Y C, Schmid G, Liu C S, Rosenbluth M N 1974 Phys. Fluids 17 778 Google Scholar
[41]	Rosenbluth M N 1972 Phys. Rev. Lett. 29 565 Google Scholar
[42]	Huo W Y, Ren G, Lan K, et al. 2010 Physics of Plasmas 17 123114 Google Scholar
[43]	Huo W Y, Lan K, Li Y, et al. 2012 Phys. Rev. Lett. 109 145004 Google Scholar
[44]	Huo W Y, Yang D, Lan K, et al. 2014 Physics of Plasmas 21 022704 Google Scholar
[45]	Xiao C Z, Zhuo H B, Yin Y, Liu Z J, Zheng C Y, Zhao Y, He X T 2018 Plasma Phys. Control. Fusion 60 025020 Google Scholar
[46]	Landau L D, Ter-Haar D 1965 Collected Papers of L.D. Landau (Oxford: Pergamon) pp445–460

施引文献

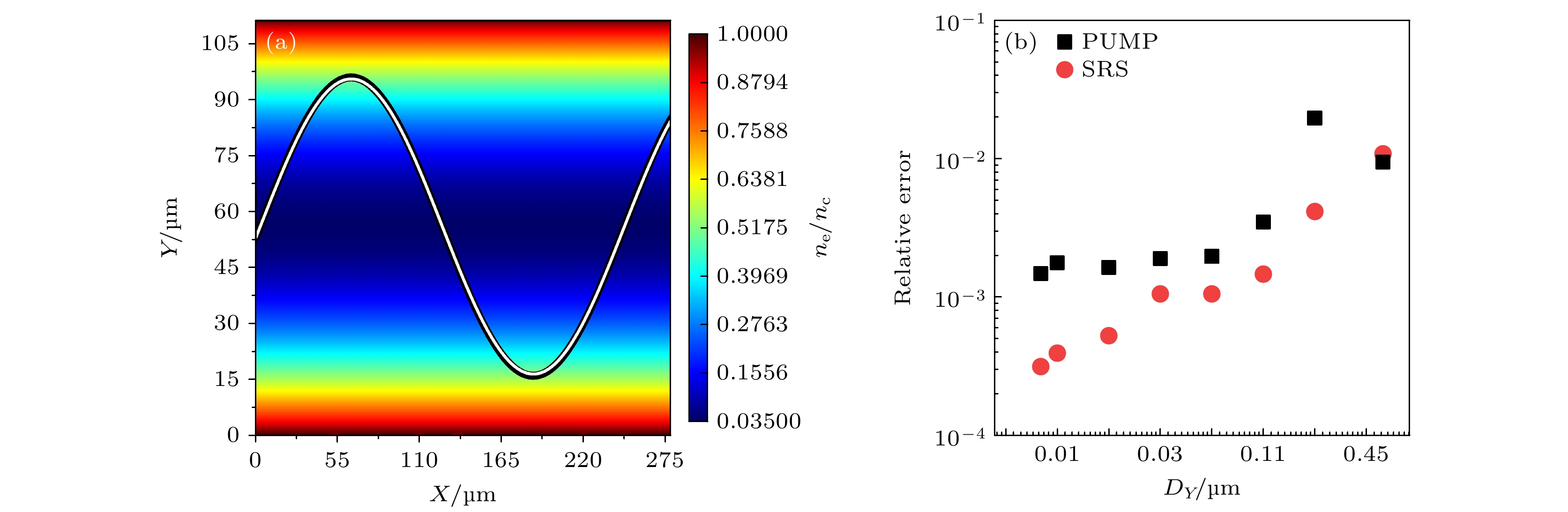
图 1 光线追踪模块校验结果　(a)入射光轨迹在等离子体中传播的轨迹图, 背景为等离子体的电子密度分布, 白线和黑线分别代表D_X = D_Y = 0.05 μm时, 入射光轨迹的模拟结果和理论结果; (b)模拟结果和理论结果在一个周期内的相对误差随D_Y的变化. D_X和D_Y分别代表X方向和Y方向的网格精度, 定义为D_X = X_max/N_X, D_Y = Y_max/N_Y, X_max, Y_max分别为X方向和Y方向的长度, N_X和N_Y则分别代表X方向和Y方向的网格数

Fig. 1. Benchmark results of the ray tracing module: (a) Pump ray trajectory of simulation (white line) and theory (black line) superimposed on the electron density with D_X = D_Y = 0.05 μm; (b) relative error between the theory and simulation results over a period vs. D_Y. The grid size D_X and D_Y are defined as D_X = X_max/N_X and D_Y = Y_max/N_Y, the X_max and Y_max are the lengths of the X and Y directions, the N_X and N_Y are the number of grids in the X and Y directions, respectively.

下载: 全尺寸图片幻灯片

图 2 (a)均匀等离子体中SRBS的增益因子$ G_{{\mathrm{B}}} $随电子温度的变化, 此时固定电子密度为$ n_{{\mathrm{e}}0} =0.05 n_{{\mathrm{c}}} $; (b) SRBS的增益因子$ G_{{\mathrm{B}}} $随电子密度的变化, 此时固定电子温度为$ T_{{\mathrm{e}}} $ = 3.0 keV

Fig. 2. (a) SRBS gain ($ G_{{\mathrm{B}}} $) vs. electron temperature for the uniform plasma for the const density $ n_{{\mathrm{e}}0} =0.05 n_{{\mathrm{c}}}$; (b) $ G_{{\mathrm{B}}} $ vs. electron density for the const temperature $ T_{{\mathrm{e}}} $ = 3.0 keV.

下载: 全尺寸图片幻灯片

图 3 SRSS的增益因子$ G_{{\mathrm{S}}} $随真空中SRSS的波长λ的变化, 其中$ \lambda = 2\pi c/ \omega_{{\mathrm{s}}} $

Fig. 3. SRSS gain ($ G_{{\mathrm{S}}} $) vs. SRSS wavelength in the vacuum (λ), $ \lambda = 2\pi c/ \omega_{{\mathrm{s}}} $.

下载: 全尺寸图片幻灯片

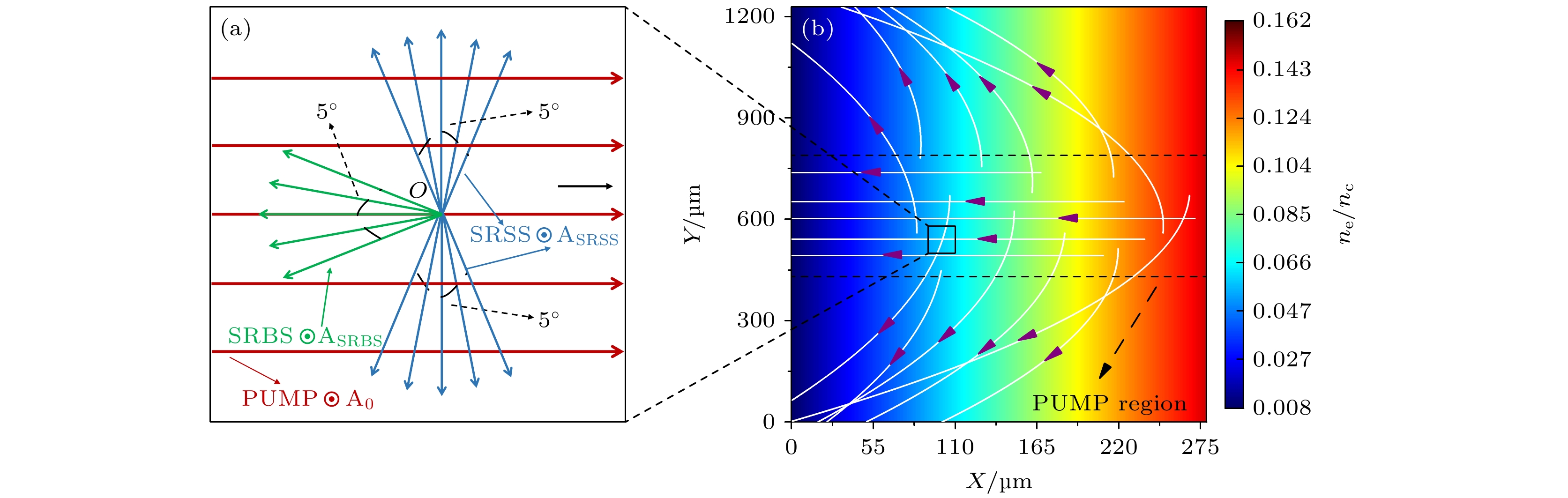
图 4 SRS散射光设置示意图　(a)散射光初始传播方向示意图, 红色箭头代表入射光的传播方向, 蓝色、绿色箭头代表SRSS和SRBS的初始传播方向, 红色、蓝色、绿色的圆圈则代表入射光、SRSS、SRBS散的偏振方向; (b)散射光传播轨迹示意图, 背景为等离子体的电子密度分布, 白色实线代表散射光的传播轨迹, 紫色的箭头代表散射光传播的方向, 黑色虚线代表入射光经过的区域

Fig. 4. Schematic of SRS configuration: (a) Schematic of the initial propagation direction of SRS, the red arrow represents the propagation direction of the incident light, the blue and green arrows represent the initial propagation direction of SRSS and SRBS, and the red, blue and green circles represent the polarisation direction of the incident light, SRSS and SRBS; (b) schematic of the SRS ray trajectory, superimposed on a plot of the electron density, the white line and violet arrow are the trajectory and direction of SRS ray, the black dashed line represents the region incident light passes.

下载: 全尺寸图片幻灯片

图 5 SRSS阈值随入射角度的变化. 蓝色线条、红色实点分别代表本文所用公式、Short所用公式计算出的阈值随入射光入射角度的变化

Fig. 5. SRSS threshold vs. incidence angle. The blue line and the red dots are the results of this article and Short, respectively.

下载: 全尺寸图片幻灯片

图 6 真空腔模拟结果　(a) SRS散射光光强的空间分布(焦斑直径取200 μm, 与Case I对应), 白色长虚线区域为SRSS光强较大的区域, 白色短点虚线区域为入射光所在区域; (b) SRS散射光光强的空间分布(焦斑直径取1200 μm, 与Case II对应); (c) SRBS频谱(D = 200 μm时与Case I对应, D = 1200 μm时与Case II对应); (d) SRSS频谱

Fig. 6. Simulation results of empty hohlraum: (a) Profile of SRS light intensity (spot diameter is taken as 200 μm, corresponds to Case I), the white dashed line is the region where the SRSS light intensity is stronger, and the white dotted line is the region where the incident light is located; (b) profile of SRS light intensity (spot diameter is taken as 1200 μm, corresponds to Case II); (c) spectrum of SRBS (D = 200 μm corresponds to Case I, and D = 1200 μm corresponds to Case II); (d) spectrum of SRSS.

下载: 全尺寸图片幻灯片

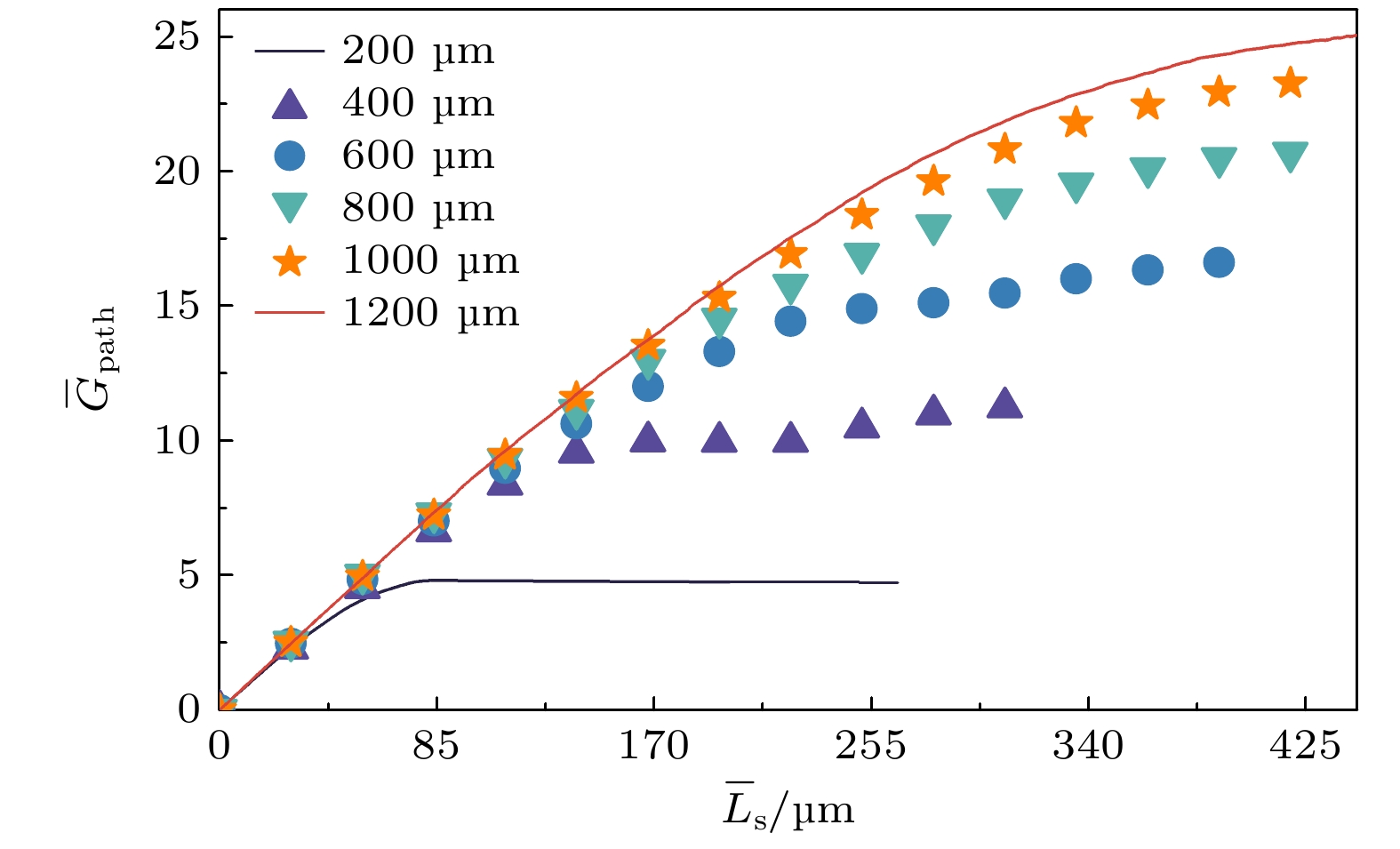
图 7 $0.1 n_{{\mathrm{c}}} $处产生的SRS的相关统计量随平均路程的变化, 实线代表SRSS, 虚线代表SRBS　(a)散射光对流增益与耦合系数随传播路程的变化; (b)入射光光强, 以及等离子体的密度和温度随传播路程的变化. 除(19)式$ \bar{G}_{{\mathrm{path}}} $外, 其余各个物理量的统计方式与$ \bar{\varGamma}_{\alpha} $保持一致, 详见(20)式

Fig. 7. Statistical physical quantities vs. average distance of SRS generated at $0.1 n_{{\mathrm{c}}} $, the solid line and the dashed line are the physical quantities of SRSS and SRBS, respectively. (a) $ \bar{G}_{{\mathrm{path}}} $ and coupling coefficient vs. average distance; (b) incident light intensity, electron density, and electron temperature of plasma vs. average distance. Statistical methods of each physical quantity are consistent with $ \bar{\varGamma}_{\alpha} $ shown in Eq. (20), except for $ \bar{G}_{{\mathrm{path}}} $ defined in Eq. (19).

下载: 全尺寸图片幻灯片

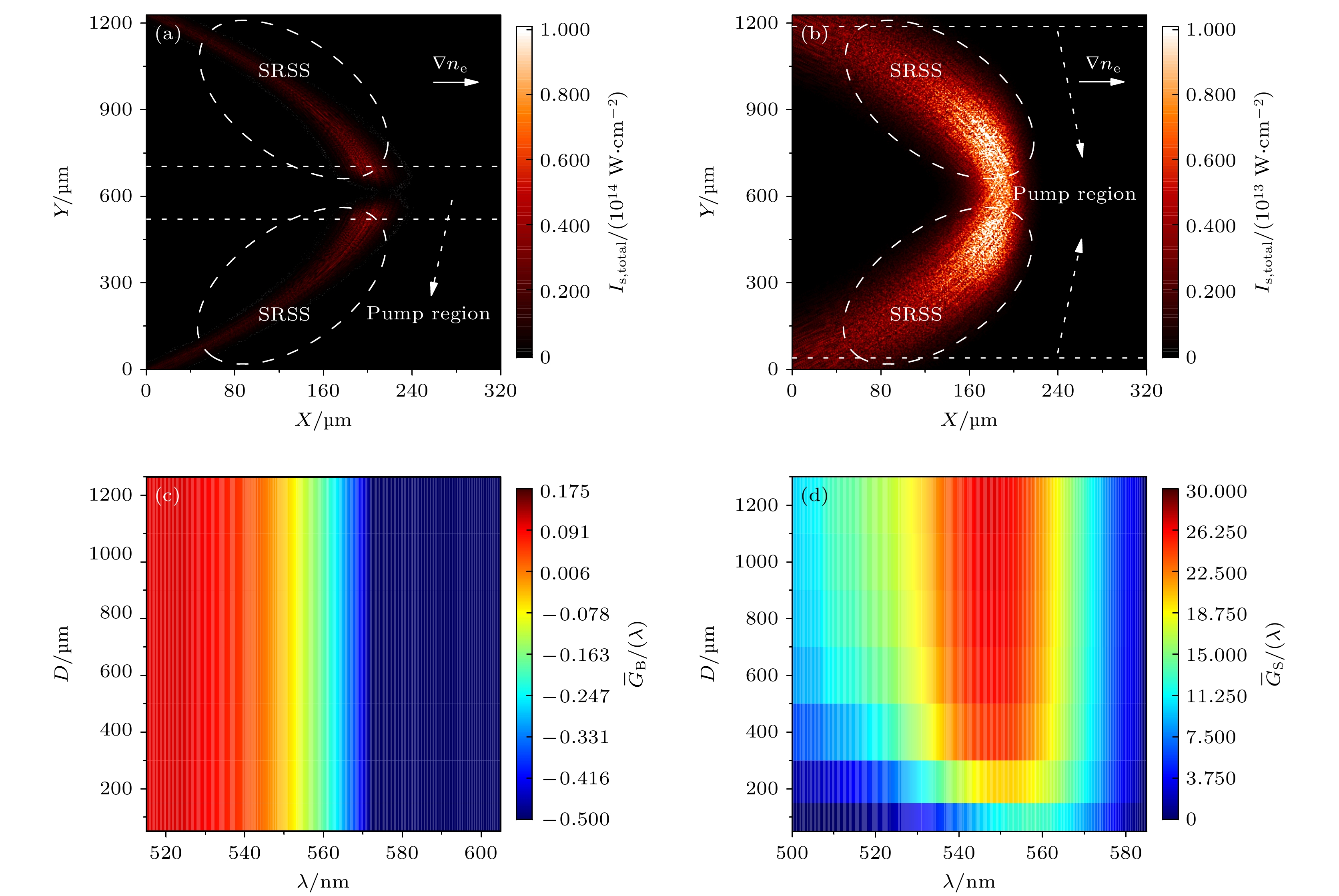
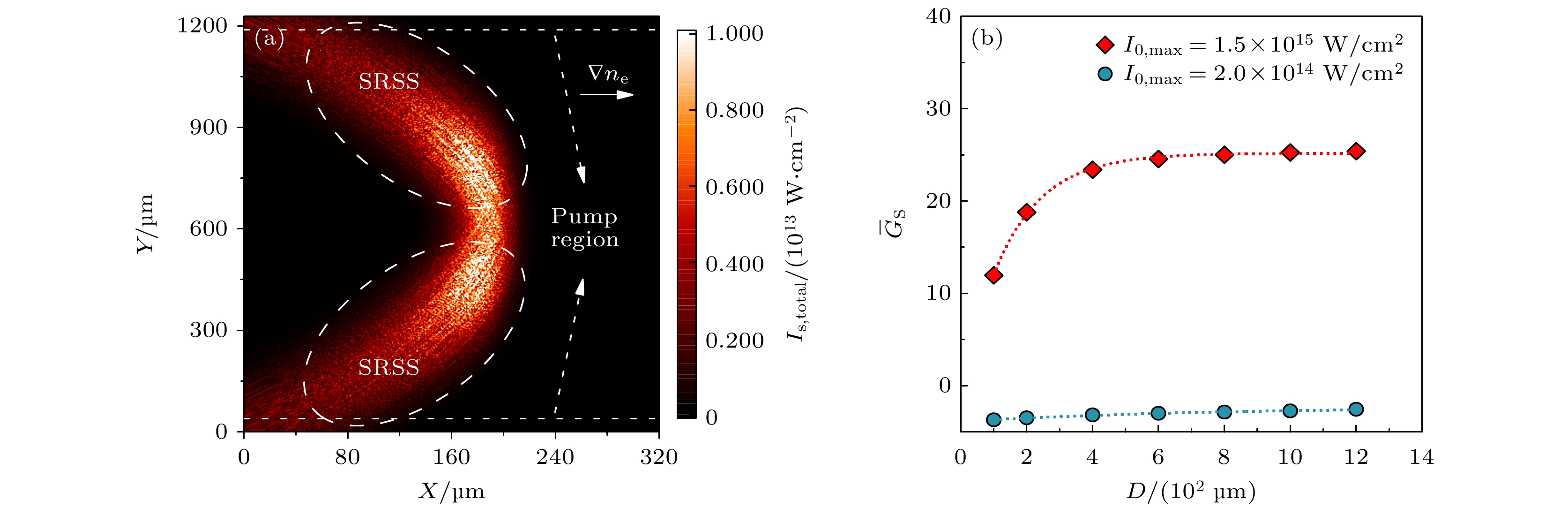
图 8 充气腔模拟结果　(a) SRS散射光光强的空间分布(焦斑直径取200 μm, 与Case III对应), 白色长虚线区域为SRSS光强较大的区域, 白色短点虚线区域为入射光所在区域; (b) SRS散射光光强的空间分布(焦斑直径取1200 μm, 与Case IV对应); (c) SRBS频谱(D = 200 μm时与Case III对应, D = 1200 μm时与Case IV对应); (d) SRSS频谱, 黑色虚线左侧为对流模区间, 而虚线右侧通常被认为是绝对模区间

Fig. 8. Simulation results of gas-filled hohlraum: (a) Profile of SRS light intensity (spot diameter is taken as 200 μm, corresponds to Case III), the white dashed line is the region where the SRSS or SRBS light intensity is stronger, and the white dotted line is the region where the incident light is located; (b) profile of SRS light intensity (spot diameter is taken as 1200 μm); (c) spectrum of SRBS (D = 200 μm corresponds to Case III, and D = 1200 μm corresponds to Case IV); (d) spectrum of SRSS, the left side of the black dotted line is convective mode dominant region, and the right side is usually treated as absolute mode region.

下载: 全尺寸图片幻灯片

图 9 充气腔在$0.05 n_{{\mathrm{c}}} $处产生的SRSS的平均增益$ \bar{G}_{{\mathrm{path}}} $在不同焦斑下随SRSS的平均路程的变化

Fig. 9. Average gain ($ \bar{G}_{{\mathrm{path}}} $) vs. average distance for SRSS generated at $ 0.05n_{{\mathrm{c}}} $ with different spot size in the gas-filled hohlraum.

下载: 全尺寸图片幻灯片

图 10 光强保持不变的条件下SRSS增益随焦斑直径的变化　(a)真空腔; (b)充气腔. 红色实点、蓝色实点分别代表不同入射光光强的模拟结果, 红色虚线、蓝色虚线则代表对数据点的拟合

Fig. 10. SRSS gain vs. spot diameter for the constant light intensity: (a) Empty hohlraum; (b) gas-filled hohlraum. The red dots and blue dots are the simulation results of different incident light intensity, the red dashed line and the blue dashed line represent the fitting results of data points, respectively.

下载: 全尺寸图片幻灯片

图 11 功率保持不变的条件下SRSS增益随焦斑直径的变化　(a)真空腔; (b)充气腔. 红色实点、蓝色实点分别代表不同入射光功率时的模拟结果, 红色虚线、蓝色虚线则代表对数据点的拟合

Fig. 11. SRSS gain vs. spot diameter for the constant power: (a) Empty hohlraum; (b) gas-filled hohlraum. The red dots and blue dots are the simulation results of different incident light power, the red dashed line and the blue dashed line represent the fitting results of data points, respectively.

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

表 1 部分模拟算例参数设置

Table 1. Parameters setting of several simulation cases.

Case $ I_{0, {\mathrm{max}}} $/(10¹⁵ W·cm^–2) D/μm 腔类型

I 1.5 200 真空腔

II 1.5 1200 真空腔

III 1.5 200 充气腔

IV 1.5 1200 充气腔

下载: 导出CSV

map

[1]	Betti R, Hurricane O A 2016 Nat. Phys. 12 435 Google Scholar
[2]	Craxton R S, Anderson K S, Boehly T R, et al. 2015 Phys. Plasmas 22 110501 Google Scholar
[3]	Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339 Google Scholar
[4]	Zylstra A B, Hurricane O A, Callahan D A, et al. 2022 Nature 601 542 Google Scholar
[5]	Abu-Shawareb H, Acree R, Adams P, et al. 2022 Phys. Rev. Lett. 129 075001 Google Scholar
[6]	Betti R 2022 Nat. Rev. Phys. 5 6 Google Scholar
[7]	Tollefson J, Gibney E 2022 Nature 612 597 Google Scholar
[8]	Hayes A C, Kyrala G, Gooden M, et al. 2023 Phys. Plasmas 30 072704 Google Scholar
[9]	Kruer W L 1988 The Physics of Laser Plasma Interactions (New York: Addison-Wesley) pp73–85
[10]	Strozzi D J, Bailey D S, Michel P, Divol L, Sepke S M, Kerbel G D, Thomas C A, Ralph J E, Moody J D, Schneider M B 2017 Phys. Rev. Lett. 118 025002 Google Scholar
[11]	Montgomery D S 2016 Phys. Plasmas 23 055601 Google Scholar
[12]	Rosenberg M J, Solodov A A, Seka W, et al. 2020 Phys. Plasmas 27 042705 Google Scholar
[13]	Yan R, Li J, Ren C 2014 Phys. Plasmas 21 062705 Google Scholar
[14]	Liu C S, Rosenbluth M N, White R B 1973 Phys. Rev. Lett. 31 697 Google Scholar
[15]	Afeyan B B, Williams E A 1985 Phys. Fluids 28 3397 Google Scholar
[16]	Figueroa H, Joshi C, Azechi H, Ebrahim N A, Estabrook K 1984 Phys. Fluids 27 1887 Google Scholar
[17]	Drake R P, Turner R E, Lasinski B F, Estabrook K G, Campbell E M, Wang C L, Phillion D W, Williams E A, Kruer W L 1984 Phys. Rev. Lett. 53 1739 Google Scholar
[18]	Drake R P, Turner R E, Lasinski B F, et al. 1988 Phys. Fluids 31 3130 Google Scholar
[19]	Renard N, Labaune C, Baldis H A, Bauer B S, Quesnel B, Schifano E, Michard A, Seka W, Estabrook K G 1996 Phys. Rev. Lett. 77 3807 Google Scholar
[20]	Michel P, Rosenberg M J, Seka W, et al. 2019 Phys. Rev. E 99 033203 Google Scholar
[21]	Rosenberg M J, Solodov A A, Myatt J F, et al. 2023 Phys. Plasmas 30 042710 Google Scholar
[22]	Depierreux S, Neuville C, Baccou C, et al. 2016 Phys. Rev. Lett. 117 235002 Google Scholar
[23]	Hironaka S, Sivajeyan J, Wang J, Rosenberg M J, Solodov A, Filkins T, Xiao C, Wang Q, Seka W, Myatt J F 2023 Phys. Plasmas 30 022708 Google Scholar
[24]	Short R W 2020 Phys. Plasmas 27 042703 Google Scholar
[25]	Michel P, Divol L, Dewald E L, Milovich J L, Hohenberger M, Jones O S, Hopkins L B, Berger R L, Kruer W L, Moody J D 2015 Phys. Rev. Lett. 115 055003 Google Scholar
[26]	Dewald E L, Hartemann F, Michel P, et al. 2016 Phys. Rev. Lett. 116 075003 Google Scholar
[27]	Moody J D, Datte P, Krauter K, et al. 2010 Rev. Sci. Instrum 81 10D921 Google Scholar
[28]	Hall G N, Jones O S, Strozzi D J, et al. 2017 Phys. Plasmas 24 052706 Google Scholar
[29]	Hao L, Zhao Y, Yang D, et al. 2014 Phys. Plasmas 21 072705 Google Scholar
[30]	Strozzi D J, Williams E A, Hinkel D E, Froula D H, London R A, Callahan D A 2008 Phys. Plasmas 15 102703 Google Scholar
[31]	龚韬 2015 博士学位论文 (合肥: 中国科学技术大学) Gong T 2015 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[32]	Xiao C Z, Wang Q, Myatt J F 2023 Phys. Rev. E 107 025203 Google Scholar
[33]	Hao L, Yang D, Li X, et al. 2019 AIP Adv. 9 095201 Google Scholar
[34]	Colaïtis A, Igumenshchev I, Mathiaud J, Goncharov V 2021 J. Comput. Phys. 443 110537 Google Scholar
[35]	Debayle A, Ruyer C, Morice O, Masson-Laborde P E, Loiseau P, Benisti D 2019 Phys. Plasmas 26 092705 Google Scholar
[36]	Colaïtis A, Follett R K, Palastro J P, Igumenschev I, Goncharov V 2019 Phys. Plasmas 26 072706 Google Scholar
[37]	Follett R K, Edgell D H, Froula D H, Goncharov V N, Igumenshchev I V, Shaw J G, Myatt J F 2017 Phys. Plasmas 24 103128 Google Scholar
[38]	Kaiser T B 2000 Phys. Rev. E 61 895 Google Scholar
[39]	Forslund D W, Kindel J M, Lindman E L 1975 Physics of Fluids 18 1002 Google Scholar
[40]	Drake J F, Kaw P K, Lee Y C, Schmid G, Liu C S, Rosenbluth M N 1974 Phys. Fluids 17 778 Google Scholar
[41]	Rosenbluth M N 1972 Phys. Rev. Lett. 29 565 Google Scholar
[42]	Huo W Y, Ren G, Lan K, et al. 2010 Physics of Plasmas 17 123114 Google Scholar
[43]	Huo W Y, Lan K, Li Y, et al. 2012 Phys. Rev. Lett. 109 145004 Google Scholar
[44]	Huo W Y, Yang D, Lan K, et al. 2014 Physics of Plasmas 21 022704 Google Scholar
[45]	Xiao C Z, Zhuo H B, Yin Y, Liu Z J, Zheng C Y, Zhao Y, He X T 2018 Plasma Phys. Control. Fusion 60 025020 Google Scholar
[46]	Landau L D, Ter-Haar D 1965 Collected Papers of L.D. Landau (Oxford: Pergamon) pp445–460

[1]	王安静, 方勇华, 李大成, 崔方晓, 吴军, 刘家祥, 李扬裕, 赵彦东. 面阵探测下的污染云团红外光谱仿真. , 2017, 66(11): 114203. doi: 10.7498/aps.66.114203
[2]	毕海亮, 魏来, 范冬梅, 郑殊, 王正汹. 旋转圆柱等离子体中撕裂模和Kelvin-Helmholtz不稳定性的激发特性. , 2016, 65(22): 225201. doi: 10.7498/aps.65.225201
[3]	郑殊, 张甲鹏, 段萍, 魏来, 王先驱. 黏滞等离子体中双撕裂模不稳定性的数值模拟研究. , 2013, 62(2): 025205. doi: 10.7498/aps.62.025205
[4]	燕飞, 张杰, 鲁欣. x射线激光传输过程中的折射和饱和效应. , 2005, 54(2): 715-720. doi: 10.7498/aps.54.715
[5]	段耀勇, 郭永辉, 王文生, 邱爱慈. Z箍缩等离子体不稳定性的数值研究. , 2004, 53(10): 3429-3434. doi: 10.7498/aps.53.3429
[6]	张家泰, 刘松芬, 胡北来. 强激光部分离化等离子体成丝不稳定性. , 2003, 52(7): 1668-1671. doi: 10.7498/aps.52.1668
[7]	黄朝松, 李钧. 等离子体交换不稳定性的模耦合理论. , 1992, 41(5): 783-791. doi: 10.7498/aps.41.783
[8]	王德真, 郭世宠, 蔡诗东. 高β等离子体中低混杂漂移不稳定性. , 1990, 39(6): 67-74. doi: 10.7498/aps.39.67-2
[9]	黄朝松, 任兆杏, 邱励俭. 热电子等离子体的耗散漂移不稳定性. , 1987, 36(9): 1112-1121. doi: 10.7498/aps.36.1112
[10]	徐学桥, 霍裕平. 托卡马克中宏观束-等离子体扭曲模不稳定性研究. , 1986, 35(10): 1259-1270. doi: 10.7498/aps.35.1259
[11]	徐至展, 林康春, 钱爱娣, 张文琦. 激光辐照等离子体中的受激布里渊侧向散射. , 1985, 34(2): 188-195. doi: 10.7498/aps.34.188
[12]	顾永年. 小环径比锐边界等离子体的扭曲模不稳定性. , 1984, 33(4): 554-560. doi: 10.7498/aps.33.554
[13]	贺贤士. 等离子体中调制不稳定性和波包的坍缩过程. , 1983, 32(5): 627-639. doi: 10.7498/aps.32.627
[14]	周玉美, 吴京生. 高β等离子体的离子-离子束不稳定性. , 1983, 32(10): 1319-1322. doi: 10.7498/aps.32.1319
[15]	王中天. 非圆截面等离子体MHD不稳定性的研究. , 1981, 30(5): 573-583. doi: 10.7498/aps.30.573
[16]	陆全康. 关于等离子体的电磁波不稳定性(Ⅱ). , 1981, 30(2): 266-270. doi: 10.7498/aps.30.266
[17]	顾永年, 邱乃贤. 椭圆截面等离子体柱的扭曲不稳定性. , 1980, 29(11): 1367-1377. doi: 10.7498/aps.29.1367
[18]	周玉美, 蔡诗东. 磁化等离子体里高频模和低频模耦合的参量不稳定性. , 1980, 29(7): 916-926. doi: 10.7498/aps.29.916
[19]	王中天. 等离子体环的竖直位移不稳定性. , 1979, 28(4): 593-598. doi: 10.7498/aps.28.593
[20]	陆全康. 关于等离子体的电磁波不稳定性. , 1964, 20(4): 289-296. doi: 10.7498/aps.20.289

计量

文章访问数: 1546
PDF下载量: 99
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

间接驱动相关条件下的大空间尺度对流受激拉曼侧向散射