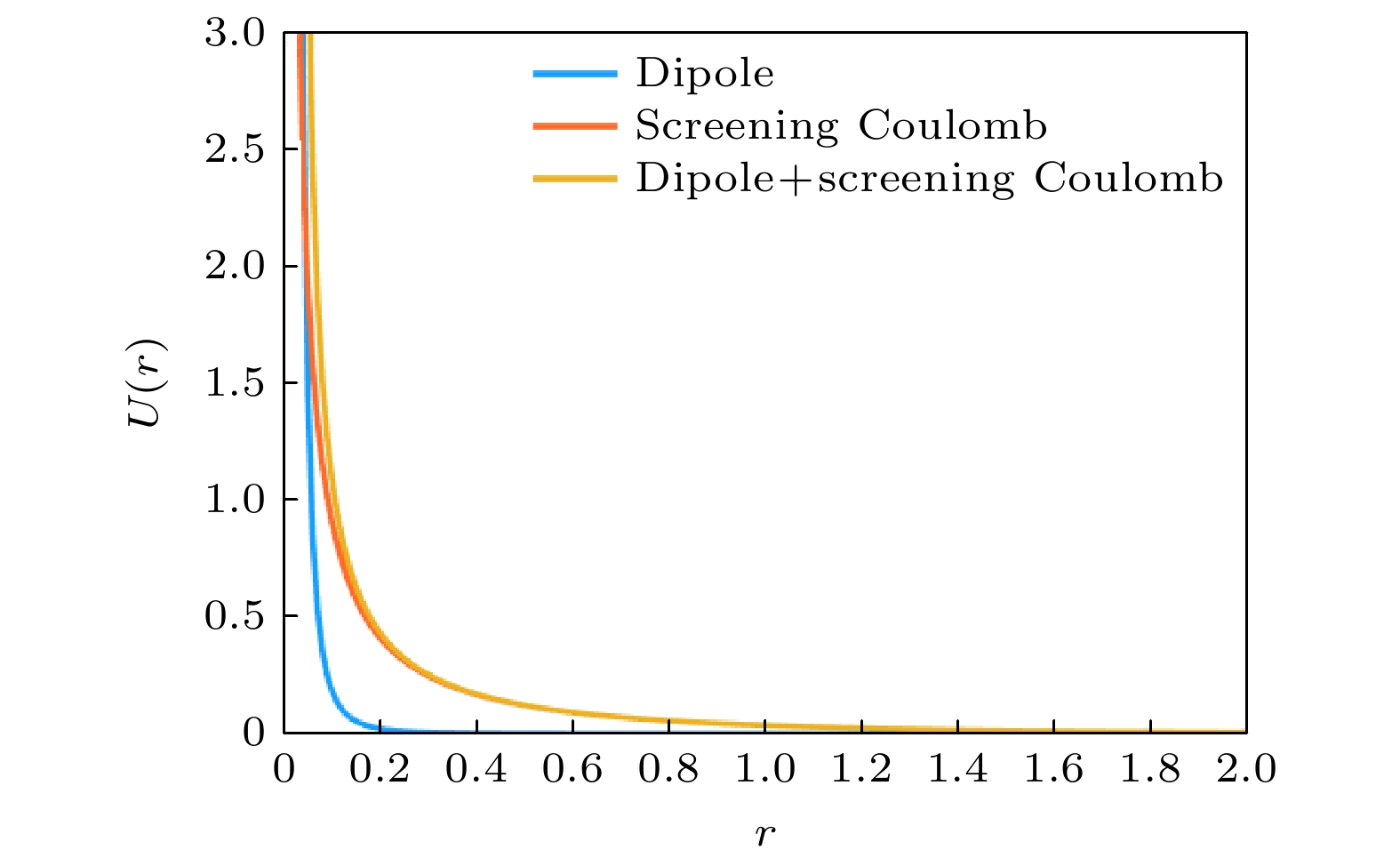
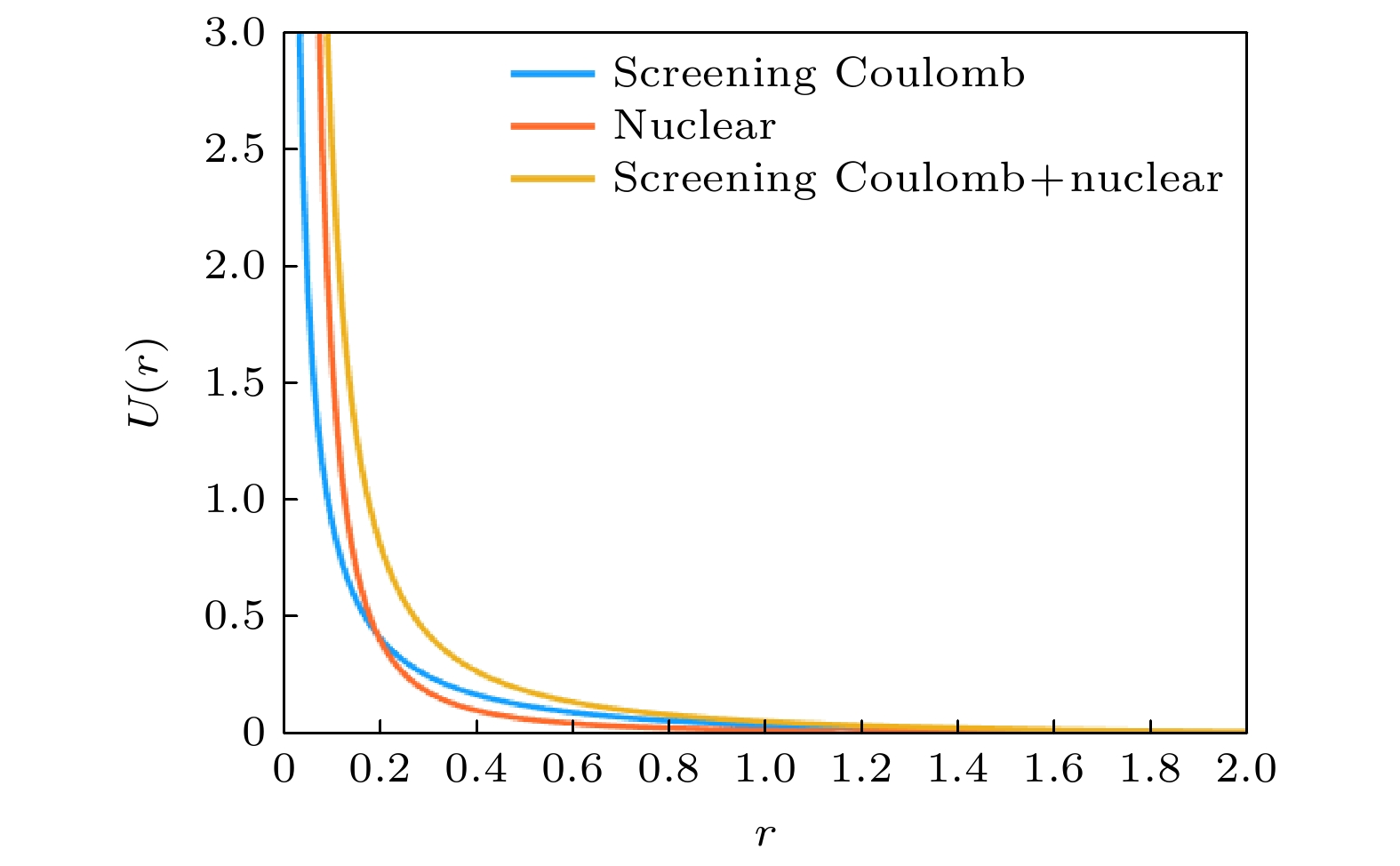
-
利用朗之万分子动力学, 数值研究了无序点钉扎衬底上二维胶体粒子系统的摩擦特性. 本文考虑了三种不同的模型胶体粒子系统, 每种系统中胶体粒子之间的相互作用均被模拟为两种不同力程的排斥势. 研究发现: 每种模型系统均存在两个最大静摩擦力(第一最大静摩擦力
$ f_{{\text{c}}1}^{\text{d}} $ 和第二最大静摩擦力$ f_{{\text{c}}2}^{\text{d}} $ ); 力程相近的短程排斥相互作用之间的干涉会导致粒子间排斥增强, 从而导致$ f_{{\text{c}}1}^{\text{d}} $ 的明显降低和$ f_{{\text{c}}2}^{\text{d}} $ 以上沿外场驱动力方向上运动有序的加强. 本文的研究结果有助于揭示具有不同力程相互作用胶体粒子系统的摩擦机制.Friction occurs in various systems from the nanoscale to the geophysical scale and plays a crucial role. The microscopic mechanism of friction and the origin of the dynamic ordering in interacting particle systems are still controversial. Using Langevin simulations, we study the friction of two-dimensional colloids on the substrate with randomly distributed point-like pinning centers. We consider three different model colloidal systems, and in each system the colloidal particles interact with each other through repulsive interactions that have two different force ranges. We find two maximum static friction forces (the first maximum static friction$ f_{{\text{c}}1}^{\text{d}} $ and the second maximum static friction$ f_{{\text{c2}}}^{\text{d}} $ ). The interference between short-range repulsive interactions with similar force ranges in model-3 colloidal system can lead the repulsion between particles near pinning centers to significantly increase, resulting in a decrease in$ f_{{\text{c}}1}^{\text{d}} $ and an enhanced orderly movement along the direction of external driving forces above$ f_{{\text{c2}}}^{\text{d}} $ . The results provide guidance for revealing the friction mechanism in the colloidal particles with interactions that have different force ranges.-
Keywords:
- friction /
- colloids /
- plastic flow /
- moving order
[1] Vanossi A, Manini N, Urbakh M, Zapperi S, Tosatti E 2013 Rev. Mod. Phys. 85 529
Google Scholar
[2] Michael U, Ernst M 2010 Nat. Mater. 9 8
Google Scholar
[3] Zhang Z Y, Wu C G, Zhang Q, Cao Y G 2020 Friction 8 666
Google Scholar
[4] Ramaswamy M, Lin N Y C, Leahy B D, Ness C, Fiore A M, Swan J W, Cohen I 2017 Phys. Rev. X 7 041005
Google Scholar
[5] Lerose A, Žunkovič B, Marino J, Gambassi A, Silva A 2019 Phys. Rev. B 99 045128
Google Scholar
[6] Driver T, Cooper B, Ayers R, Pipkorn R, Patchkovskii S, Averbukh V, Klug D R, Marangos J P, Frasinski L J, Edelson-Averbukh M 2020 Phys. Rev. X 10 041004
Google Scholar
[7] Marchetti M C, Joanny J F, Ramaswamy S, Liverpool T B, Prost J, Rao M, Simha R A 2013 Rev. Mod. Phys. 85 1143
Google Scholar
[8] Zhang T H, Kuipers B W M, Tian W D, Groenewold J, Kege W K 2015 Soft Matter 11 297
Google Scholar
[9] Gilpin W, Bull M S, Prakash M 2020 Nat. Rev. Phys. 2 74
Google Scholar
[10] Arora P, Sood A K, Ganapathy R 2021 Sci. Adv. 7 eabd0331
Google Scholar
[11] Chen J X, Chen G Y, Kapral R 2018 Sci. Adv. 5 1800028
Google Scholar
[12] Cui R F, Chen Q H, Chen J X 2020 Nanoscale 12 12275
Google Scholar
[13] Mognetti B M, Šarić A, Angioletti-Uberti S, Cacciuto A, Valeriani C, Frenkel D 2013 Phys. Rev. Lett. 111 245702
Google Scholar
[14] Solon A P, Stenhammar J, Wittkowski R, Kardar M, Kafri Y, Cates M E, Tailleur J 2015 Phys. Rev. Lett. 114 198301
Google Scholar
[15] Cao T T, Li Z, Lü W L, Cao Y G 2017 J. Phys. Commun. 1 045008
Google Scholar
[16] Alshareedah I, Kaur T, Ngo J, Seppala H, Kounatse L D, Wang W, Moosa M M, Banerjee P R 2019 J. Am. Chem. Soc. 141 14593
Google Scholar
[17] Mondal M, Mishra C K, Banerjee R, Narasimhan S, Sood A K, Ganapathy R 2020 Sci. Adv. 6 eaay8418
Google Scholar
[18] Theurkauff I, Cottin-Bizonne C, Palacci J, Ybert C, Bocquet L 2012 Phys. Rev. Lett. 108 268303
Google Scholar
[19] Velasco A C, Abkenar M, Gompper G, Auth T 2018 Phys. Rev. E 98 022605
Google Scholar
[20] Rudner M S, Lindner N H 2020 Nat. Rev. Phys. 2 229
Google Scholar
[21] Wittmann R, Brader J M, Sharma A, Marconi U M B 2018 Phys. Rev. E 97 012601
Google Scholar
[22] Skou M G, Skov T G, Jorgensen N B, Nielsen K K, Camacho-Guardian A, Pohl T, Bruun G M, Arlt J J 2021 Nat. Phys. 17 731
Google Scholar
[23] Digregorio P, Levis D, Pagonabarraga I 2018 Phys. Rev. Lett. 121 098003
Google Scholar
[24] Park J, Zhao H B, Kang S D, Lim K, Chen C C, Yu Y S, Braatz R D, Shapiro D A, Hong J, Toney M F, Bazant M Z, Chueh W C 2021 Nat. Mater. 20 991
Google Scholar
[25] Chubak I, Likos C N, Kremer K, Smrek J 2020 Phys. Rev. Res. 2 043249
Google Scholar
[26] Shi X Q, Fausti G, Chaté H, Nardini C, Solon A 2020 Phys. Rev. Lett. 125 168001
Google Scholar
[27] Chattoraj J, Ciamarra M P 2020 Phys. Rev. Lett. 124 028001
Google Scholar
[28] Malescio G, Pellicane G 2003 Nat. Mater. 2 97
Google Scholar
[29] Delfau J B, Ollivier H, López C, Blasius B, Hernández-García E 2016 Phys. Rev. E 94 042120
Google Scholar
[30] Daza F A G, Cuetos A, Patti A 2020 Phys. Rev. E 102 013302
Google Scholar
[31] Li X D, Wu C G, Cao T T, Cao Y G 2019 Physica A 515 279
Google Scholar
[32] Fisher D S 1980 Phys. Rev. B 22 1190
Google Scholar
-
图 1 三种模型胶体粒子系统中粒子间相互作用势随粒子间距离的变化
Fig. 1. Distance dependences of the interaction potentials in three model systems.
图 2 库仑势、磁偶极子势以及库仑+磁偶极子势随距离的函数关系曲线
Fig. 2. Distance dependences of the Coulomb, magnetic dipole and Coulomb + magnetic dipole potentials.
图 3 磁偶极子势、屏蔽库仑势以及磁偶极子+屏蔽库仑势随距离的函数关系曲线
Fig. 3. Distance dependences of the magnetic dipole, screening Coulomb and magnetic dipole + screening Coulomb potentials.
图 4 屏蔽库仑势、排斥核势以及屏蔽库仑+排斥核势随距离的函数关系曲线
Fig. 4. Distance dependences of the screening Coulomb, nuclear and screening Coulomb + nuclear potentials.
图 6 模型1 (a), (a′)、模型2 (b), ( b′)和模型3 (c), (c′)中, 胶体粒子分别在第一最大静摩擦力$ f_{{\text{c}}1}^{\text{d}} $下方(a)—(c)和上方(a′)—(c′)的位形快照, 钉扎中心用×号表示
Fig. 6. Snapshots of particle coordinates below (a)–(c) and above (a′)–(c′) the first maximum static friction $f_{{\mathrm{c}}1}^{\mathrm{d}}$ for models 1 (a), (a′), 2 (b), ( b′) and 3 (c), (c′). The pinning centers are denoted by crosses.
图 7 模型1 ((a), (a′))、模型2 ((b), (b′))和模型3 ((c), (c′))胶体粒子系统在第二最大静摩擦力$f_{{\mathrm{c}}2}^{\mathrm{d}}$之上的运动位形和结构因子
Fig. 7. Flow trajectories of particles and corresponding structure factors along $x$ direction above the second maximum static friction $f_{{\mathrm{c}}2}^{\mathrm{d}}$ for model 1 ((a) and (a′)), model 2 ((b) and (b′)) and model 3 ((c) and (c′)) systems, respectively.
-
[1] Vanossi A, Manini N, Urbakh M, Zapperi S, Tosatti E 2013 Rev. Mod. Phys. 85 529
Google Scholar
[2] Michael U, Ernst M 2010 Nat. Mater. 9 8
Google Scholar
[3] Zhang Z Y, Wu C G, Zhang Q, Cao Y G 2020 Friction 8 666
Google Scholar
[4] Ramaswamy M, Lin N Y C, Leahy B D, Ness C, Fiore A M, Swan J W, Cohen I 2017 Phys. Rev. X 7 041005
Google Scholar
[5] Lerose A, Žunkovič B, Marino J, Gambassi A, Silva A 2019 Phys. Rev. B 99 045128
Google Scholar
[6] Driver T, Cooper B, Ayers R, Pipkorn R, Patchkovskii S, Averbukh V, Klug D R, Marangos J P, Frasinski L J, Edelson-Averbukh M 2020 Phys. Rev. X 10 041004
Google Scholar
[7] Marchetti M C, Joanny J F, Ramaswamy S, Liverpool T B, Prost J, Rao M, Simha R A 2013 Rev. Mod. Phys. 85 1143
Google Scholar
[8] Zhang T H, Kuipers B W M, Tian W D, Groenewold J, Kege W K 2015 Soft Matter 11 297
Google Scholar
[9] Gilpin W, Bull M S, Prakash M 2020 Nat. Rev. Phys. 2 74
Google Scholar
[10] Arora P, Sood A K, Ganapathy R 2021 Sci. Adv. 7 eabd0331
Google Scholar
[11] Chen J X, Chen G Y, Kapral R 2018 Sci. Adv. 5 1800028
Google Scholar
[12] Cui R F, Chen Q H, Chen J X 2020 Nanoscale 12 12275
Google Scholar
[13] Mognetti B M, Šarić A, Angioletti-Uberti S, Cacciuto A, Valeriani C, Frenkel D 2013 Phys. Rev. Lett. 111 245702
Google Scholar
[14] Solon A P, Stenhammar J, Wittkowski R, Kardar M, Kafri Y, Cates M E, Tailleur J 2015 Phys. Rev. Lett. 114 198301
Google Scholar
[15] Cao T T, Li Z, Lü W L, Cao Y G 2017 J. Phys. Commun. 1 045008
Google Scholar
[16] Alshareedah I, Kaur T, Ngo J, Seppala H, Kounatse L D, Wang W, Moosa M M, Banerjee P R 2019 J. Am. Chem. Soc. 141 14593
Google Scholar
[17] Mondal M, Mishra C K, Banerjee R, Narasimhan S, Sood A K, Ganapathy R 2020 Sci. Adv. 6 eaay8418
Google Scholar
[18] Theurkauff I, Cottin-Bizonne C, Palacci J, Ybert C, Bocquet L 2012 Phys. Rev. Lett. 108 268303
Google Scholar
[19] Velasco A C, Abkenar M, Gompper G, Auth T 2018 Phys. Rev. E 98 022605
Google Scholar
[20] Rudner M S, Lindner N H 2020 Nat. Rev. Phys. 2 229
Google Scholar
[21] Wittmann R, Brader J M, Sharma A, Marconi U M B 2018 Phys. Rev. E 97 012601
Google Scholar
[22] Skou M G, Skov T G, Jorgensen N B, Nielsen K K, Camacho-Guardian A, Pohl T, Bruun G M, Arlt J J 2021 Nat. Phys. 17 731
Google Scholar
[23] Digregorio P, Levis D, Pagonabarraga I 2018 Phys. Rev. Lett. 121 098003
Google Scholar
[24] Park J, Zhao H B, Kang S D, Lim K, Chen C C, Yu Y S, Braatz R D, Shapiro D A, Hong J, Toney M F, Bazant M Z, Chueh W C 2021 Nat. Mater. 20 991
Google Scholar
[25] Chubak I, Likos C N, Kremer K, Smrek J 2020 Phys. Rev. Res. 2 043249
Google Scholar
[26] Shi X Q, Fausti G, Chaté H, Nardini C, Solon A 2020 Phys. Rev. Lett. 125 168001
Google Scholar
[27] Chattoraj J, Ciamarra M P 2020 Phys. Rev. Lett. 124 028001
Google Scholar
[28] Malescio G, Pellicane G 2003 Nat. Mater. 2 97
Google Scholar
[29] Delfau J B, Ollivier H, López C, Blasius B, Hernández-García E 2016 Phys. Rev. E 94 042120
Google Scholar
[30] Daza F A G, Cuetos A, Patti A 2020 Phys. Rev. E 102 013302
Google Scholar
[31] Li X D, Wu C G, Cao T T, Cao Y G 2019 Physica A 515 279
Google Scholar
[32] Fisher D S 1980 Phys. Rev. B 22 1190
Google Scholar
下载:
计量
- 文章访问数: 1212
- PDF下载量: 21
- 被引次数: 0
