-
基于单电子有效质量近似理论和传递矩阵方法, 理论研究了稀磁半导体/半导体超晶格结构中电子的自旋极化输运特性. 主要讨论了光场和磁场联合调制对自旋极化输运的影响, 以及不同自旋电子在该超晶格结构中的隧穿时间. 理论和数值计算结果表明, 由于导带电子与掺杂Mn 离子之间的sp-d 电子相互作用引起巨塞曼劈裂, 因此在磁场调制下, 不同自旋电子在该结构中感受到的势函数不同而呈现出自旋过滤效应, 不同自旋电子的共振透射能带的位置和宽度可以通过磁场进行调制. 同时在该结构中考虑光场时, 自旋依赖的透射谱会因为吸收和发射光子而呈现出对光场的强度和频率响应; 最后, 通过不同自旋电子的高斯波包在该结构中随时间的演化给出了不同自旋电子的隧穿时间. 本文研究结果对研究和设计基于稀磁半导体/半导体超晶格结构的高速量子器件具有一定的指导意义.
-
关键词:
- 自旋极化输运 /
- 稀磁半导体/半导体超晶格 /
- 隧穿时间
Based on the single electron effective mass approximation theory and the transfer-matrix method, the spin polarized transport properties of electrons in a diluted-magnetic-semiconductor/semiconductor superlattice are studied. The influence of a light-field and a magnetic-field on spin polarized transport and the tunneling time in the superlattice structure are discussed in more detail. The results show that, due to the sp-d electron interaction between conduction band electrons and doped Mn ions, giant Zeeman splitting occurs. It is shown that a significant spin-dependent transmission and the position and width of the resonant-transmission-band of spin-dependent electron can be manipulated by adjusting the magnetic- and light-field. Considering the light field irradiation, the resonance band of electron is deformed and broadened with the increase of the light field intensity. For the case of a strong magnetic field, the transmission coefficient (TC) in the low-energy region is almost zero when the light field is not added, but with the increase of light intensity, the TC increased significantly in the zone increases significantly, that is, a quasi-bound band appears. These features are due to the energy exchange between electrons and the light field when electrons tunnel through the superlattice structure under light irradiation. In addition, light and magnetic fields can significantly change the spin polarization of electrons. Under a certain magnetic field intensity (B = 2 T), the light field significantly changes the spin polarization of electrons, the main effect is that the width of the spin polarization platform narrows and oscillatory peaks are accompanied on both sides of the platform. This effect is strengthened with the increase of the light field intensity. However, when the magnetic field is stronger (B = 5 T), the opposite is true. These show that the spin polarization can be modulated by the light field. Finally, the tunneling time of spin-up and spin-down electrons is studied by the evolution of Gaussian wave packets in the structure. The results show that the tunneling time depends on a spin of electrons, and it can be seen that the tunneling time of the spin-down electron is shorter than that of the spin-up electron in the superlattice structure. These remarkable properties of spin polarized transport may be beneficial for the devising tunable spin filtering devices based on diluted magnetic semiconductor/semiconductor superlattice structure.-
Keywords:
- spin polarized transport /
- diluted magnetic semiconductors/semiconductors superlattices /
- tunneling time
[1] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, Von Molnar S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[2] Egues J C 1998 Phys. Rev. Lett. 80 4578
Google Scholar
[3] Chang K, Peeters F M 2001 Solid State Commun. 120 181
Google Scholar
[4] Slobodskyy A, Gould C, Slobodskyy T, Becker C R, Schmidt G, Molenkamp L W 2003 Phys. Rev. Lett. 90 246601
Google Scholar
[5] Hijano A, Bergeret F S, Giazotto F, Braggio A 2023 Phys. Rev. Appl. 19 044024
Google Scholar
[6] Zhu Z G, Su G 2004 Phys. Rev. B 70 193310
Google Scholar
[7] Zhai F, Guo Y, Gu B L 2003 J. Appl. Phys. 94 5432
Google Scholar
[8] Yang P F, Zhu R, Guo Y 2015 AIP Advances 5 077115
Google Scholar
[9] Furdyna J K 1988 J. Appl. Phys. 64 R29
Google Scholar
[10] Papp G, Borza S, Peeters F M 2005 J. Appl. Phys. 97 113901
Google Scholar
[11] Chishti S S, Ghosh B, Verma A, Salimath A K 2014 J. Nanoelectron. Optoe 9 44
Google Scholar
[12] Evropeytsev E A, Klimko G V, Komissarova T A, et al. 2014 Semiconductors 48 30
Google Scholar
[13] Ming Y, Gong J, Zhang R Q 2011 J. Appl. Phys. 110 093717
Google Scholar
[14] Havu P, Tuomisto N, Väänänen R, Puska M J, Nieminen R M 2005 Phys. Rev. B 71 235301
Google Scholar
[15] Wójcik P, Adamowski J, Wołoszyn M, Spisak B J 2012 Phys. Rev. B 86 165318
Google Scholar
[16] Gruber T H, Keim M, Fiederling R, Reuscher G, Ossau W, Schmidt G, Molenkamp L W, Waag A 2001 Appl. Phys. Lett. 78 1101
Google Scholar
[17] Schmidt G, Richter G, Grabs P, Gould C, Ferrand D, Molenkamp L W 2001 Phys. Rev. Lett. 87 227203
Google Scholar
[18] Schmidt G, Gould C, Grabs P, Lunde A M, Richter G, Slobodskyy A, Molenkamp L W 2004 Phys. Rev. Lett. 92 226602
Google Scholar
[19] Guo Y, Wang H, Gu B L, Kawazoe Y 2000 J. Appl. Phys. 88 6614
Google Scholar
[20] Guo Y, Chen X Y, Zhai F, Gu B L, Kawazoe Y 2002 Appl. Phys. Lett. 80 4591
Google Scholar
[21] Guo Y, Shen F R, Chen X Y 2012 Appl. Phys. Lett. 101 012410
Google Scholar
[22] 张存喜, 王瑞, 孔令民 2010 59 4980
Google Scholar
Zhang C X, Wang R, Kong L M 2010 Acta Phys. Sin. 59 4980
Google Scholar
[23] Li C L, Ruan R Y, Guo Y 2016 J. Appl. Phys. 119 014306
Google Scholar
[24] Dayem A H, Martin R J 1962 Phys. Rev. Lett. 8 246
Google Scholar
[25] Tien P K, Gordon J P 1963 Phys. Rev. 129 647
Google Scholar
[26] Sun Q F, Wang J, Lin T H 2000 Phys. Rev. B 61 12643
Google Scholar
[27] Bruder C, Schoeller H 1994 Phys. Rev. Lett. 72 1076
Google Scholar
[28] Shibata K, Umeno A, Cha K M, Hirakawa K 2012 Phys. Rev. Lett. 109 077401
Google Scholar
[29] Schoelkopf R J, Kozhevnikov A A, Prober D E 1998 Phys. Rev. Lett. 80 2437
Google Scholar
[30] König B, Zehnder U, Yakovlev D R, Ossau W, Gerhard T, Keim M, Waag A, Landwehr G 1999 Phys. Rev. B 60 2653
Google Scholar
[31] Harada N, Kuroda S 1986 Jap. J. Appl.Phys. 25 L871
Google Scholar
[32] 曾谨言 2000 量子力学(上卷) (北京: 科学出版社) 第721页
Zeng J Y 2000 Quantum Mechanics (Vol. 1) (Beijing: Science Press) p721
-
图 1 光场
$ V_{1}\mathrm{cos}(\omega t) $ 辐照下自旋相关$ {\rm ZnSe}/{\rm Zn}_{1-x}{\rm Mn}_{x}{\rm Se} $ 超晶格势 (a)$ B = 5 $ T; (b)$ B = 2 $ TFig. 1. Spin-dependent potential profiles of the
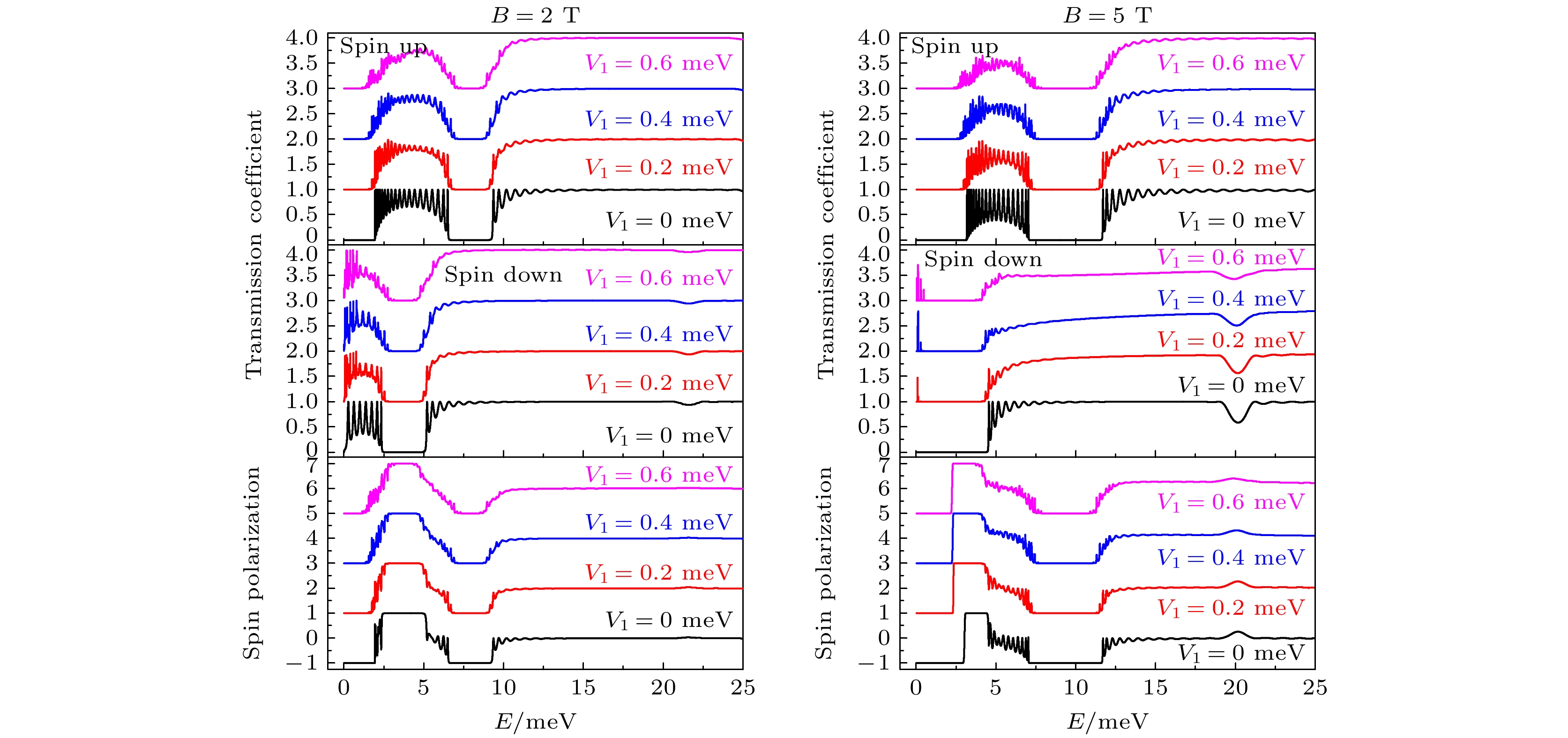
$ {\rm ZnSe}/ $ $ {\rm Zn}_{1-x}{\rm Mn}_{x}{\rm Se} $ superlattice under a light field$ V_{1}\mathrm{cos}(\omega t) $ : (a)$ B = 5 $ T; (b)$ B = 2 $ T.
图 2 光场辐照下, 不同磁场强度电子自旋相关透射系数和自旋极化度, 其中光子能量
$ \hbar \omega = 0.2 $ meV, 光场强度$ V_{1} = 0, $ $ 0.2, \;0.4, \;0.6 $ meVFig. 2. Spin-dependent transmission coefficients and spin polarization for different magnetic induction intensity under the light field, where the energy of photon is
$ \hbar \omega = 0.2 $ meV, and amplitude of the light field is$ V_{1} = 0,\; 0.2,\; 0.4,\; 0.6 $ meV.
图 3 稀磁半导体/半导体超晶格结构中, 不同时刻不同自旋方向电子概率密度
$ |\psi(z, t)|^{2} $ 随坐标z的变化关系曲线 (a)自旋向上; (b) 自旋向下Fig. 3. Spin-dependent electron probability density
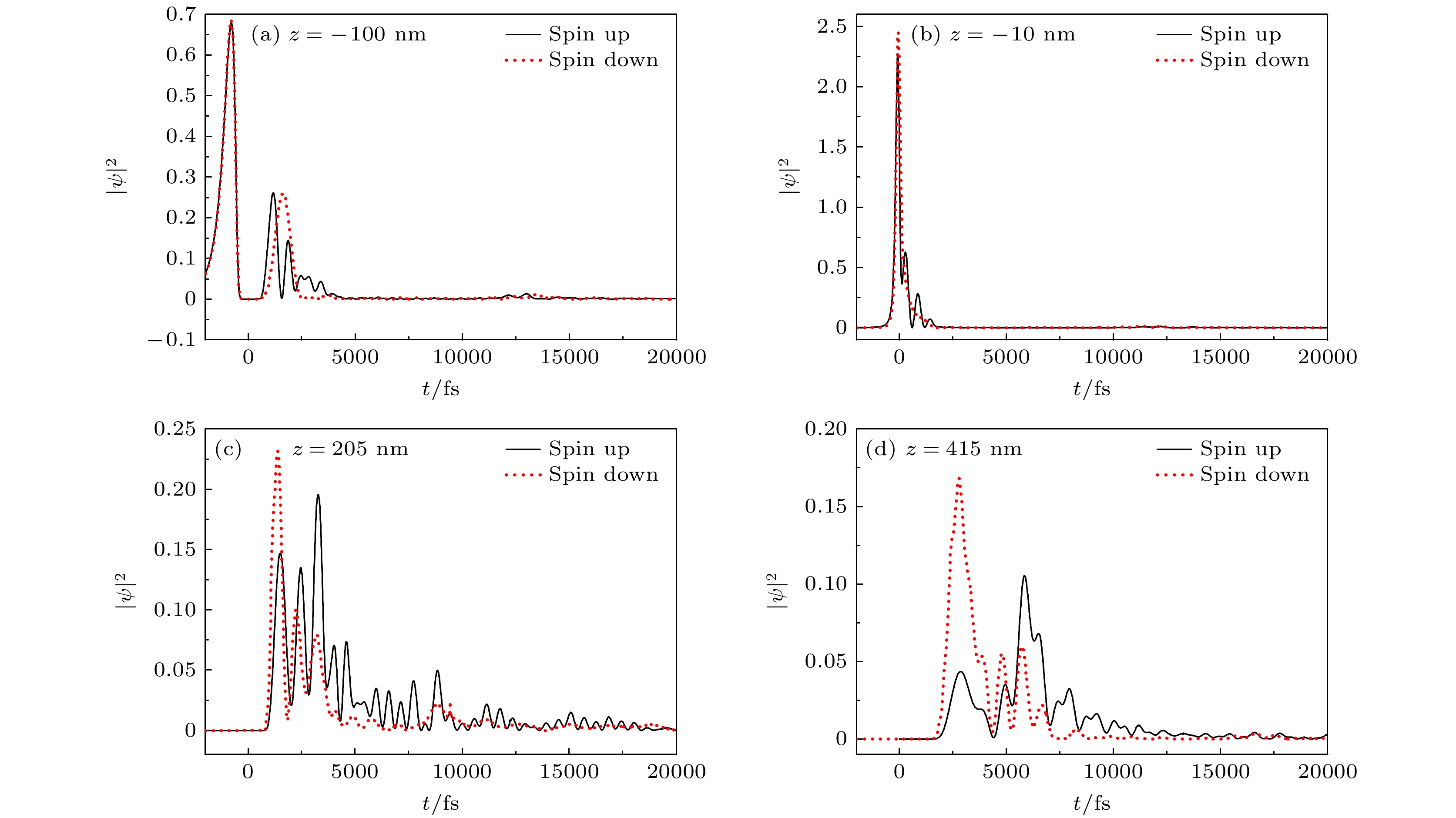
$ |\psi(z, t)|^{2} $ as a function of coordinate z for different times in the superlattices of dilute magnetic semiconductors/semiconductors structure: (a) Spin up; (b) spin down.
图 4 稀磁半导体/半导体(DMS/S) 超晶格结构中, 位置
$ z=-100,\; -10, \;205,\; 415 $ nm 处, 不同自旋方向电子概率密度$ |\psi(z, t)|^{2} $ 随时间t的变化关系曲线Fig. 4. Spin-dependent electron probability density
$ |\psi(z, t)|^{2} $ as a function of time t for different coordinates$ z=-100, \;-10, $ $ 205, \;415 $ nm in the superlattices of dilute magnetic semiconductors/semiconductors structure. -
[1] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, Von Molnar S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488
Google Scholar
[2] Egues J C 1998 Phys. Rev. Lett. 80 4578
Google Scholar
[3] Chang K, Peeters F M 2001 Solid State Commun. 120 181
Google Scholar
[4] Slobodskyy A, Gould C, Slobodskyy T, Becker C R, Schmidt G, Molenkamp L W 2003 Phys. Rev. Lett. 90 246601
Google Scholar
[5] Hijano A, Bergeret F S, Giazotto F, Braggio A 2023 Phys. Rev. Appl. 19 044024
Google Scholar
[6] Zhu Z G, Su G 2004 Phys. Rev. B 70 193310
Google Scholar
[7] Zhai F, Guo Y, Gu B L 2003 J. Appl. Phys. 94 5432
Google Scholar
[8] Yang P F, Zhu R, Guo Y 2015 AIP Advances 5 077115
Google Scholar
[9] Furdyna J K 1988 J. Appl. Phys. 64 R29
Google Scholar
[10] Papp G, Borza S, Peeters F M 2005 J. Appl. Phys. 97 113901
Google Scholar
[11] Chishti S S, Ghosh B, Verma A, Salimath A K 2014 J. Nanoelectron. Optoe 9 44
Google Scholar
[12] Evropeytsev E A, Klimko G V, Komissarova T A, et al. 2014 Semiconductors 48 30
Google Scholar
[13] Ming Y, Gong J, Zhang R Q 2011 J. Appl. Phys. 110 093717
Google Scholar
[14] Havu P, Tuomisto N, Väänänen R, Puska M J, Nieminen R M 2005 Phys. Rev. B 71 235301
Google Scholar
[15] Wójcik P, Adamowski J, Wołoszyn M, Spisak B J 2012 Phys. Rev. B 86 165318
Google Scholar
[16] Gruber T H, Keim M, Fiederling R, Reuscher G, Ossau W, Schmidt G, Molenkamp L W, Waag A 2001 Appl. Phys. Lett. 78 1101
Google Scholar
[17] Schmidt G, Richter G, Grabs P, Gould C, Ferrand D, Molenkamp L W 2001 Phys. Rev. Lett. 87 227203
Google Scholar
[18] Schmidt G, Gould C, Grabs P, Lunde A M, Richter G, Slobodskyy A, Molenkamp L W 2004 Phys. Rev. Lett. 92 226602
Google Scholar
[19] Guo Y, Wang H, Gu B L, Kawazoe Y 2000 J. Appl. Phys. 88 6614
Google Scholar
[20] Guo Y, Chen X Y, Zhai F, Gu B L, Kawazoe Y 2002 Appl. Phys. Lett. 80 4591
Google Scholar
[21] Guo Y, Shen F R, Chen X Y 2012 Appl. Phys. Lett. 101 012410
Google Scholar
[22] 张存喜, 王瑞, 孔令民 2010 59 4980
Google Scholar
Zhang C X, Wang R, Kong L M 2010 Acta Phys. Sin. 59 4980
Google Scholar
[23] Li C L, Ruan R Y, Guo Y 2016 J. Appl. Phys. 119 014306
Google Scholar
[24] Dayem A H, Martin R J 1962 Phys. Rev. Lett. 8 246
Google Scholar
[25] Tien P K, Gordon J P 1963 Phys. Rev. 129 647
Google Scholar
[26] Sun Q F, Wang J, Lin T H 2000 Phys. Rev. B 61 12643
Google Scholar
[27] Bruder C, Schoeller H 1994 Phys. Rev. Lett. 72 1076
Google Scholar
[28] Shibata K, Umeno A, Cha K M, Hirakawa K 2012 Phys. Rev. Lett. 109 077401
Google Scholar
[29] Schoelkopf R J, Kozhevnikov A A, Prober D E 1998 Phys. Rev. Lett. 80 2437
Google Scholar
[30] König B, Zehnder U, Yakovlev D R, Ossau W, Gerhard T, Keim M, Waag A, Landwehr G 1999 Phys. Rev. B 60 2653
Google Scholar
[31] Harada N, Kuroda S 1986 Jap. J. Appl.Phys. 25 L871
Google Scholar
[32] 曾谨言 2000 量子力学(上卷) (北京: 科学出版社) 第721页
Zeng J Y 2000 Quantum Mechanics (Vol. 1) (Beijing: Science Press) p721
下载:
计量
- 文章访问数: 1876
- PDF下载量: 59
- 被引次数: 0
