-
High-energy nuclear physics aims to explore and understand the physics of matter composed of quarks and gluons. However, it is intrinsically difficult to simulate high-energy nuclear physics from the first principle based quantum chromodynamics by using classical computers. In recent years, quantum computing has received intensive attention because it is expected to provide an ultimate solution for simulating high-energy nuclear physics. In this paper, we firstly review recent advances in quantum simulation of high-energy nuclear physics. Then we introduce some standard quantum algorithms, such as state preparation and measurements of light-cone correlation function. Finally, we demonstrate the advantage of quantum computing for solving the real-time evolution and the sign problems by studying hadronic scattering amplitude and phase structure of finite-temperature and finite-density matter, respectively.
-
Keywords:
- high-energy nuclear physics /
- quantum algorithm /
- scattering amplitude /
- phase structure of nuclear matter
[1] Alexandru A, Basar G, Bedaque P F, Vartak S, Warrington N C 2016 Phys. Rev. Lett. 117 081602
Google Scholar
[2] Troyer M, Wiese U J 2005 Phys. Rev. Lett. 94 170201
Google Scholar
[3] Feynman R P 1982 Int. J. Theor. Phys. 21 467
Google Scholar
[4] Jordan S P, Lee K S M, Preskill J 2012 Science 336 1130
Google Scholar
[5] Lamm H, Lawrence S, Yamauchi Y 2020 Phys. Rev. Res. 2 013272
Google Scholar
[6] Mueller N, Tarasov A, Venugopalan R 2020 Phys. Rev. D 102 016007
Google Scholar
[7] Echevarria M G, Egusquiza I L, Rico E, Schnell G 2021 Phys. Rev. D 104 014512
[8] Qian W, Basili R, Pal S, Luecke G, Vary J P 2022 Phys. Rev. Res. 4 043193
Google Scholar
[9] Li T, Guo X, Lai W K, Liu X, Wang E, Xing H, Zhang D B, Zhu S L 2022 Phys. Rev. D 10 5
[10] Li T, Guo X, Lai W K, Liu X, Wang E, Xing H, Zhang D B, Zhu S L 2023 Science China Physics, Mechanics & Astronomy 66 281011
[11] Bauer C W, de Jong W A, Nachman B, Provasoli D 2021 Phys. Rev. Lett. 126 062001
Google Scholar
[12] Bepari K, Malik S, Spannowsky M, Williams S 2022 Phys. Rev. D 106 056002
Google Scholar
[13] Hu Z, Xia R, Kais S 2020 Sci. Rep. 10 3301
Google Scholar
[14] De Jong W A, Metcalf M, Mulligan J, Płoskoń M, Ringer F, Yao X 2021 Phys. Rev. D 104 051501
[15] Yao X 2022 arXiv: 2205.07902 [High Energy Physics-Phenomenology
[16] Zhou Z Y, Su G X, Halimeh J C, Ott R, Sun H, Hauke P, Yang B, Yuan Z S, Berges J, Pan J W 2022 Science 377 abl6277
[17] de Jong W A, Lee K, Mulligan J, Płoskoń M, Ringer F, Yao X 2022 Phys. Rev. D 106 054508
[18] Briceño R A, Guerrero J V, Hansen M T, Sturzu A M 2021 Phys. Rev. D 103 014506
[19] Li T, Lai W K, Wang E, Xing H 2023 arXiv: 2301.04179 [High Energy Physics - Phenomenology
[20] Martinez E A, Muschik C A, Schindler M, et al. 2016 Nature 534 516
Google Scholar
[21] Atas Y Y, Haase J F, Zhang J, Wei V, Pfaendler S M L, Lewis R, Muschik C A 2022 arXiv: 2207.03473 [Quantum Physics
[22] Czajka A M, Kang Z B, Ma H, Zhao F 2022 JHEP 08 209
[23] Davoudi Z, Mueller N, Powers C 2022 arXiv: 2208.13112 [High Energy Physics - Lattice
[24] Tomiya A 2023 PoS LATTICE2022 039
[25] Czajka A M, Kang Z B, Tee Y, Zhao F 2022 arXiv: 2210.03062 [High Energy Physics - Phenomenology
[26] Xie X D, Guo X, Xing H, Xue Z Y, Zhang D B, Zhu S L 2022 Phys. Rev. D 106 054509
[27] McClean J R, Kimchi-Schwartz M E, Carter J, de Jong W A 2017 Phys. Rev. A 95 042308
Google Scholar
[28] Nakanishi K M, Mitarai K, Fujii K 2019 Phys. Rev. Res. 1 033062
Google Scholar
[29] Higgott O, Wang D, Brierley S 2019 Quantum 3 156
Google Scholar
[30] Zhang D B, Yuan Z H, Yin T 2020 arXiv: 2006.15781 [Quantum Physics
[31] Bärtschi A, Eidenbenz S 2019 In Gąsieniec L A, Jansson J, Levcopoulos C, editors, Fundamentals of Computation Theory (Cham: Springer International Publishing) pp126–139
[32] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [Quantum Physics
[33] Wiersema R, Zhou C, de Sereville Y, Carrasquilla J F, Kim Y B, Yuen H 2020 PRX Quantum 1 020319
Google Scholar
[34] Zhang D B, Zhang G Q, Xue Z Y, Zhu S L, Wang Z 2021 Phys. Rev. Lett 127 020502
Google Scholar
[35] Francis A, Zhu D, Huerta Alderete C, Johri S, Xiao X, Freericks J K, Monroe C, Linke N M, Kemper A F 2021 Sci. Adv. 7 eabf2447
Google Scholar
[36] Verdon G, Marks J, Nanda S, Leichenauer S, Hidary J 2019 arXiv: 1910.02071 [Quantum Physics
[37] Wu J, Hsieh T H 2019 Phys. Rev. Lett 123 220502
Google Scholar
[38] Zhu D, Johri S, Linke N M, Landsman K, Alderete C H, Nguyen N H, Matsuura A, Hsieh T, Monroe C 2020 Proc. Natl. Acad. Sci. 117 25402
Google Scholar
[39] Martyn J, Swingle B 2019 Phys. Rev. A 100 032107
Google Scholar
[40] Kliesch M, Gogolin C, Kastoryano M J, Riera A, Eisert J 2014 Phys. Rev. X 4 031019
[41] Pedernales J S, Di Candia R, Egusquiza I L, Casanova J, Solano E 2014 Phys. Rev. Lett. 113 020505
Google Scholar
[42] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge: Cambridge University Press) pp206–208
[43] Lin H W, Nocera E R, Olness F, et al. 2018 Prog. Part. Nucl. Phys. 100 107
Google Scholar
[44] Gao J, Harland-Lang L, Rojo J 2018 Phys. Rep. 742 1
Google Scholar
[45] Lepage G P, Brodsky S J 1980 Phys. Rev. D 22 2157
Google Scholar
[46] Efremov A V, Radyushkin A V 1980 Phys. Lett. B 94 245
Google Scholar
[47] Ji X 2013 Phys. Rev. Lett. 110 262002
Google Scholar
[48] Ji X 2014 Sci. China Phys. Mech. Astron. 57 1407
Google Scholar
[49] Ma Y Q, Qiu J W 2018 Phys. Rev. D 98 074021
Google Scholar
[50] Ma Y Q, Qiu J W 2018 Phys. Rev. Lett. 120 022003
Google Scholar
[51] Radyushkin A V 2017 Phys. Rev. D 96 034025
Google Scholar
[52] Orginos K, Radyushkin A, Karpie J, Zafeiropoulos S 2017 Phys. Rev. D 96 094503
[53] Liang J, Draper T, Liu K F, Rothkopf A, Yang Y B 2020 Phys. Rev. D 101 114503
Google Scholar
[54] Chambers A J, Horsley R, Nakamura Y, Perlt H, Rakow P E L, Schierholz G, Schiller A, Somfleth K, Young R D, Zanotti J M 2017 Phys. Rev. Lett. 118 242001
Google Scholar
[55] Sufian R S, Karpie J, Egerer C, Orginos K, Qiu J W, Richards D G 2019 Phys. Rev. D 99 074507
Google Scholar
[56] Izubuchi T, Jin L, Kallidonis C, Karthik N, Mukherjee S, Petreczky P, Shugert C, Syritsyn S 2019 Phys. Rev. D 100 034516
Google Scholar
[57] Lin H W, Chen J W, Fan Z, Zhang J H, Zhang R 2021 Phys. Rev. D 103 014516
[58] Musch B U, Hagler P, Engelhardt M, Negele J W, Schafer A 2012 Phys. Rev. D 85 094510
[59] Detmold W, Melnitchouk W, Negele J W, Renner D B, Thomas A W 2001 Phys. Rev. Lett. 87 172001
Google Scholar
[60] Hagler Ph, Schroers W, Bratt J, et al. 2008 Phys. Rev. D 77 094502
[61] Alexandrou C, Constantinou M, Dinter S, Drach V, Hadjiyiannakou K, Jansen K, Koutsou G, Vaquero A 2015 JHEP 06 068
[62] Alexandrou C, Bacchio S, Constantinou M, Finkenrath J, Hadjiyiannakou K, Jansen K, Koutsou G, Panagopoulos H, Spanoudes G 2020 Phys. Rev. D 101 094513
[63] Zhang J H, Chen J W, Ji X, Jin L, Lin H W 2017 Phys. Rev. D 95 094514
[64] Zhang J H, Jin L, Lin H W, Schäfer A, Sun P, Yang Y B, Zhang R, Zhao Y, Chen J W 2019 Nucl. Phys. B 939 429
Google Scholar
[65] Hua J, Chu M H, Sun P, Wang W, Xu J, Yang Y B, Zhang J H, Zhang Q A 2021 Phys. Rev. Lett. 127 062002
Google Scholar
[66] Hua J, Chu M H, He J C, et al. 2022 Phys. Rev. Lett. 129 132001
Google Scholar
[67] Luscher M 1986 Commun. Math. Phys. 105 153
Google Scholar
[68] Luscher M 1991 Nucl. Phys. B 354 531
Google Scholar
[69] Briceno R A, Dudek J J, Young R D 2018 Rev. Mod. Phys. 90 025001
Google Scholar
[70] Davoudi Z 2018 PoS LATTICE 2018 014
[71] Hansen M T, Sharpe S R 2019 Ann. Rev. Nucl. Part. Sci. 69 65
Google Scholar
[72] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 124 246
Google Scholar
[73] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 122 345
Google Scholar
[74] Gross D J, Neveu A 1974 Phys. Rev. D 10 3235
Google Scholar
[75] Backens S, Shnirman A, Makhlin Y 2019 Sci. Rep. 9 2
[76] Weinberg P, Bukov M 2017 SciPost Phys. 2 003
Google Scholar
[77] Steiger D S, Häner T, Troyer M 2018 Quantum 2 49
Google Scholar
[78] Collins J 2013 Foundations of Perturbative QCD (Cambridge: Cambridge University Press) pp174–176
[79] Ishikawa T, Jin L, Lin H W, Schäfer A, Yang Y B, Zhang J H, Zhao Y 2019 Sci. China Phys. Mech. Astron. 62 991021
Google Scholar
[80] Jia Y, Liang S, Xiong X, Yu R 2018 Phys. Rev. D 98 054011
Google Scholar
[81] Barry P C, Ji C R, Sato N, Melnitchouk W 2021 Phys. Rev. Lett. 127 232001
Google Scholar
[82] Chernyak V L, Zhitnitsky A R 1984 Phys. Rep. 112 173
Google Scholar
[83] Zhang R, Honkala C, Lin H W, Chen J W 2020 Phys. Rev. D 102 094519
[84] Jordan S P, Lee K S M, Preskill J 2014 Quant. Inf. Comput. 14 1014
[85] Jordan S P, Lee K S M, Preskill J 2014 arXiv: 1404.7115 [High Energy Physics-Theory
[86] Lehmann H, Symanzik H, Zimmerman W 1955 Nuovo Cimento 1 205
Google Scholar
[87] Abdalla E, Abdalla M C B, Rothe K D 1991 Non-perturbative Methods in 2D Quantum Field Theory (Singaproe: World Scientific Publishing House
[88] Lowenstein J, Swieca J 1971 Ann. Phys. 68 172
Google Scholar
[89] Byrnes T, Sriganesh P, Bursill R, Hamer C 2002 Phys. Rev. D 66 013002
Google Scholar
[90] Buyens B, Montangero S, Haegeman J, Verstraete F, Van Acoleyen K 2017 Phys. Rev. D 95 094509
[91] Zinn-Justin J 2002 In New Developments in Quantum Field Theory (Springer), pp217–232
[92] Kogut J, Susskind L 1975 Phys. Rev. D 11 395
[93] Fetter A L, Walecka J D 2012 Quantum Theory of Many-particle Systems (New York: Courier Corporation
[94] Casher A, Kogut J, Susskind L 1974 Phys. Rev. D 10 732
Google Scholar
[95] Hamer C, Kogut J, Crewther D, Mazzolini M 1982 Nucl. Phys. B 208 413
Google Scholar
[96] Buyens B, Verstraete F, Van Acoleyen K 2016 Phys. Rev. D 94 085018
Google Scholar
[97] Johansson J R, Nation P D, Nori F 2012 Comput. Phys. Commun. 183 1760
Google Scholar
[98] Pisarski R D, Alvarez O 1982 Phys. Rev. D 26 3735
Google Scholar
[99] Fodor Z, Katz S D 2004 J. High Energy Phys. 2004 050
[100] D’ Elia M, Lombardo M P 2003 Phys. Rev. D 67 014505
[101] Allton C R, Ejiri S, Hands S J, Kaczmarek O, Karsch F, Laermann E, Schmidt C 2003 Phys. Rev. D 68 014507
-
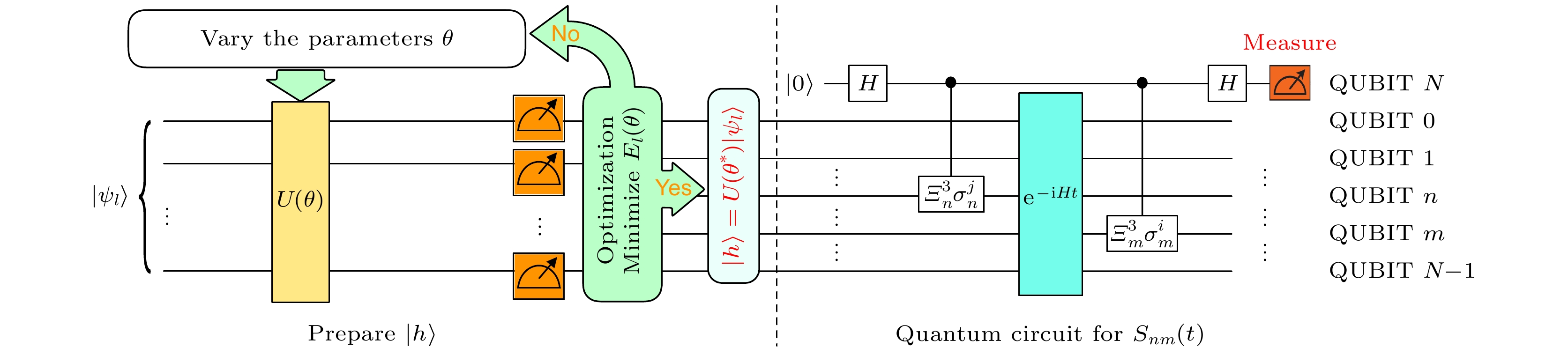
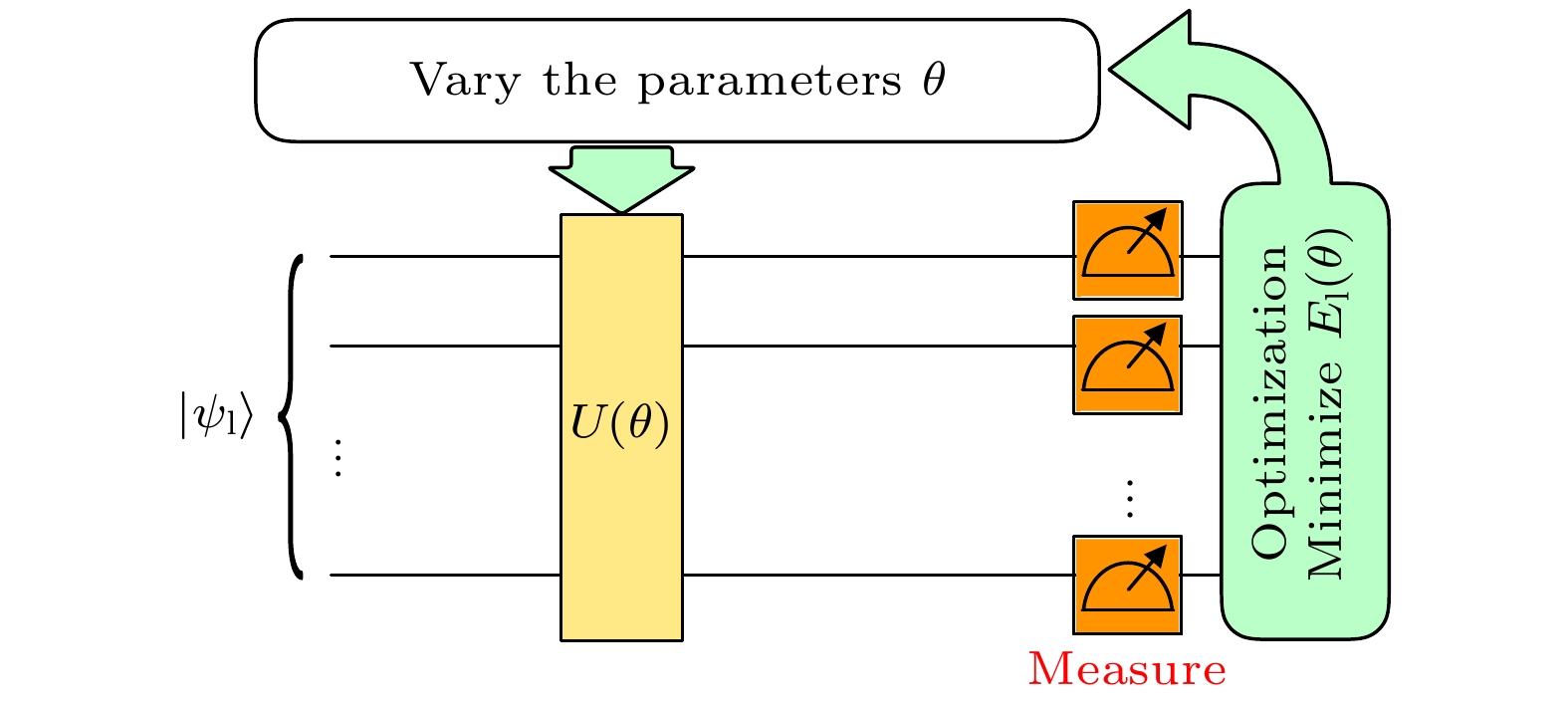
图 1 变分法制备强子态的量子线路图. 其中量子计算机通过拟设U(θ)来生成试探波函数以及测量试探波函数下
$ E_l(\theta) $ 的值. 经典计算机负责更新和优化参数θFig. 1. Variational quantum algorithm for preparation of the hadronic state. The generation of trial state and the measurement of
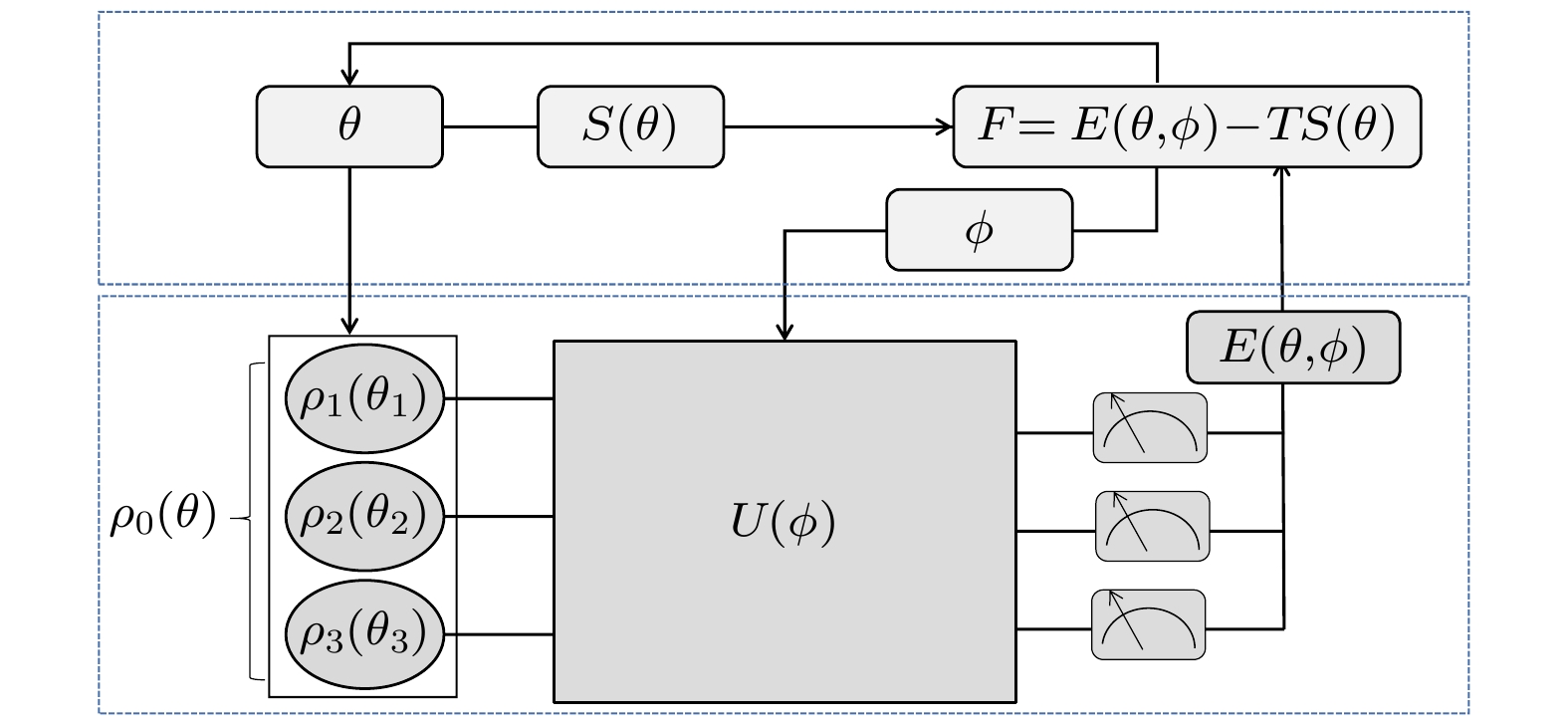
$ E_l(\theta) $ are performed on a quantum computer, while the optimization of parameters θ is done with classical computing.
图 2 可同时制备吉布斯态和计算自由能的变分算法量子线路图. 在量子计算机中执行的是初始混态的制备和参数化幺正演化
$ U(\phi) $ , 而参数$ (\theta, \phi) $ 的优化通过经典计算机来执行Fig. 2. A pictorial representation of the variational quantum algorithm, which can prepare thermal states and compute the corresponding free energy. The preparation of initial mixed state and the evolution
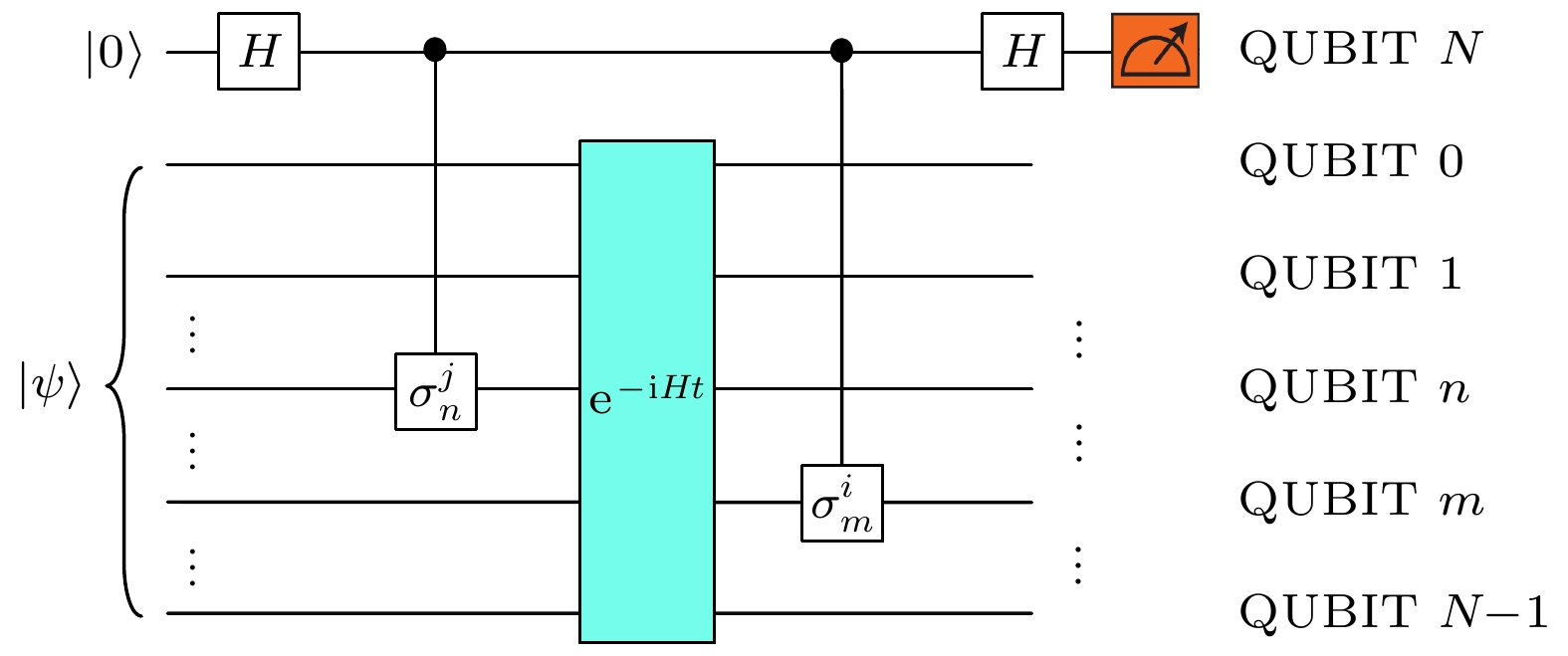
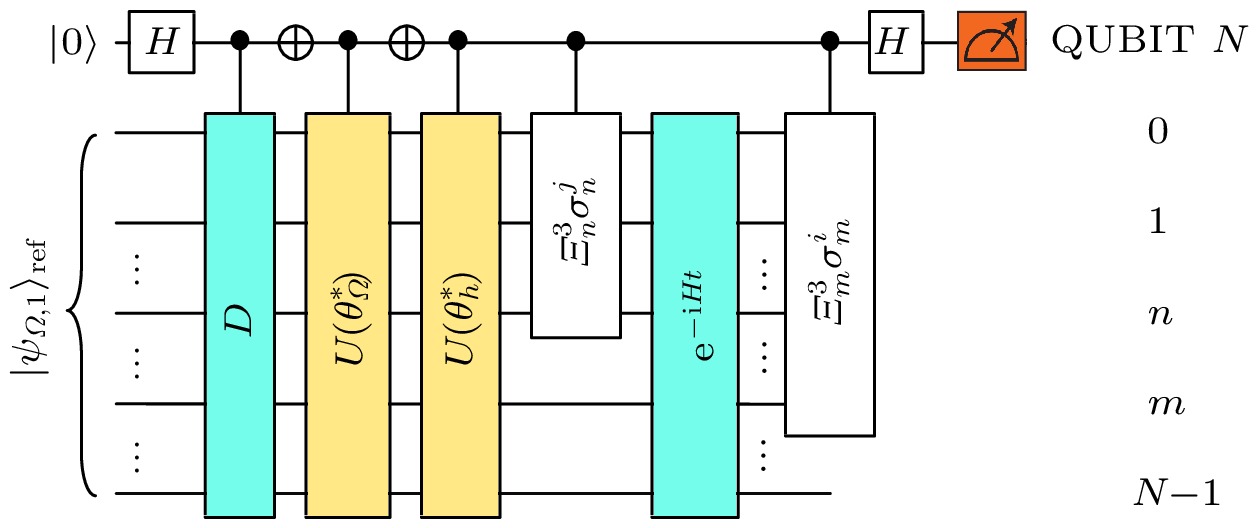
$ U(\phi) $ are done on a quantum computer, while the optimization of$ (\theta, \phi) $ should be done with a classical computer.
图 3 计算动力学两点关联函数量子线路. 在辅助比特上测量
$ \sigma^1 $ 和$ \sigma^2 $ 即可得到关联函数的实部和虚部Fig. 3. Quantum circuit for calculation of the two point correlation function. The real and imaginary part of the correlation function can be obtained by performing measurements of
$ \sigma^1 $ and$ \sigma^2 $ on the auxiliary qubit, respectively.
图 4 部分子分布计算的量子线路. 其中虚线左边部分为制备强子态的量子线路, 右边部分为测量动力学两点关联函数线路
Fig. 4. Quantum circuit for calculation of PDFs. The left side of the dashed line of the circuit is for hadronic state preparation, while the right side is for the correlation function.
图 5 坐标空间夸克场两点关联函数的实部(实线)和虚部(虚线), 其中离散的点是格点计算给出的数值, 线由格点数据结果插值得到
Fig. 5. Real (dashed lines) and imaginary parts (solid lines) of the quark correlation function in position space. The discrete points are the lattice data and the lines are obtained by interpolations.
图 6 量子计算经典模拟获得的PDF(空心点)和格点NJL模型精确对角化获得的PDF(实线), 其中不同插值方法带来的误差由误差棒标记出
Fig. 6. The quark PDF from quantum computing (open markers) and ED (solid lines). The error bars/bands arise from the estimated uncertainties due to different interpolation methods.
图 7 模拟左矢为真空, 右矢为强子的光锥关联函数
$\langle\varOmega|{\cal{O}}| h\rangle$ 的量子线路图Fig. 7. Quantum circuit for the light-cone correlator
$ \langle\varOmega|{\cal{O}}| h\rangle $ 
图 8 1+1维NJL模型LCDA对耦合常数g的依赖, 其中固定
$ N=14 $ ,$ m_{\rm{h}}=1.5 a^{-1} $ Fig. 8. LCDA for the 1+1 dimensional NJL model with
$ N = 14 $ ,$ m_{\rm{h}} = 1.5a^{-1} $ .
图 9 1+1维NJL模型LCDA对强子质量
$ m_{\rm{h}} $ 的依赖, 其中固定$ N=14 $ ,$ g=0.1 $ Fig. 9. Dependence of the LCDA on the hadron mass
$ m_{\rm{h}} $ with fixed bare coupling$ g=0.1 $ in the 1+1 dimensional NJL model
图 10 1+1维NJL模型
$ {\rm Tr}K_\Psi(p) $ 的实部. 图中以$ p^0 $ 为变量, 固定$ p^1=0 $ Fig. 10. Real part of
$ {\rm Tr}K_\Psi(p) $ for the 1+1-dimensional NJL model as a function of$ p^0 a $ with$ p^1=0 $ .
图 11 1+1维单味道NJL模型四点函数
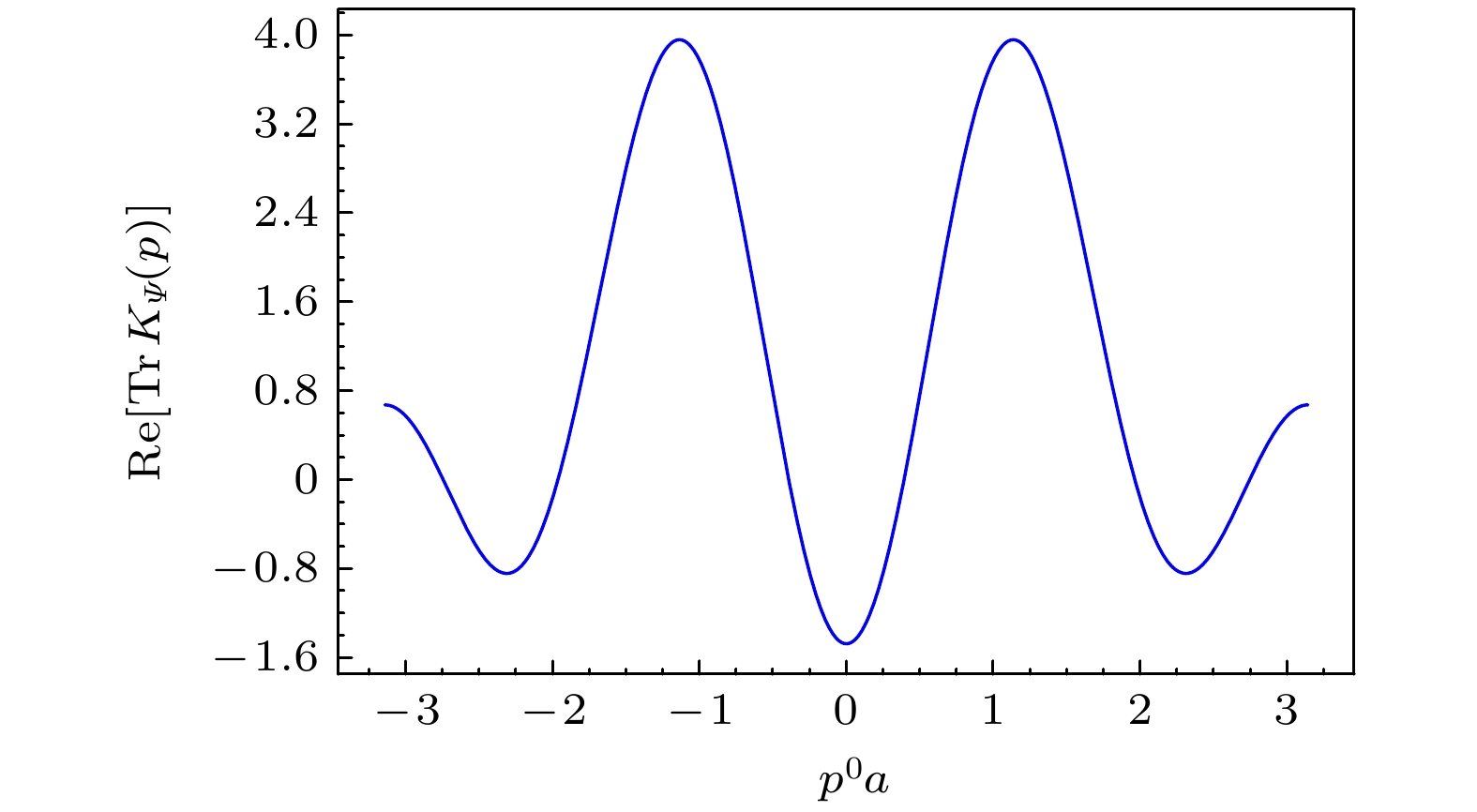
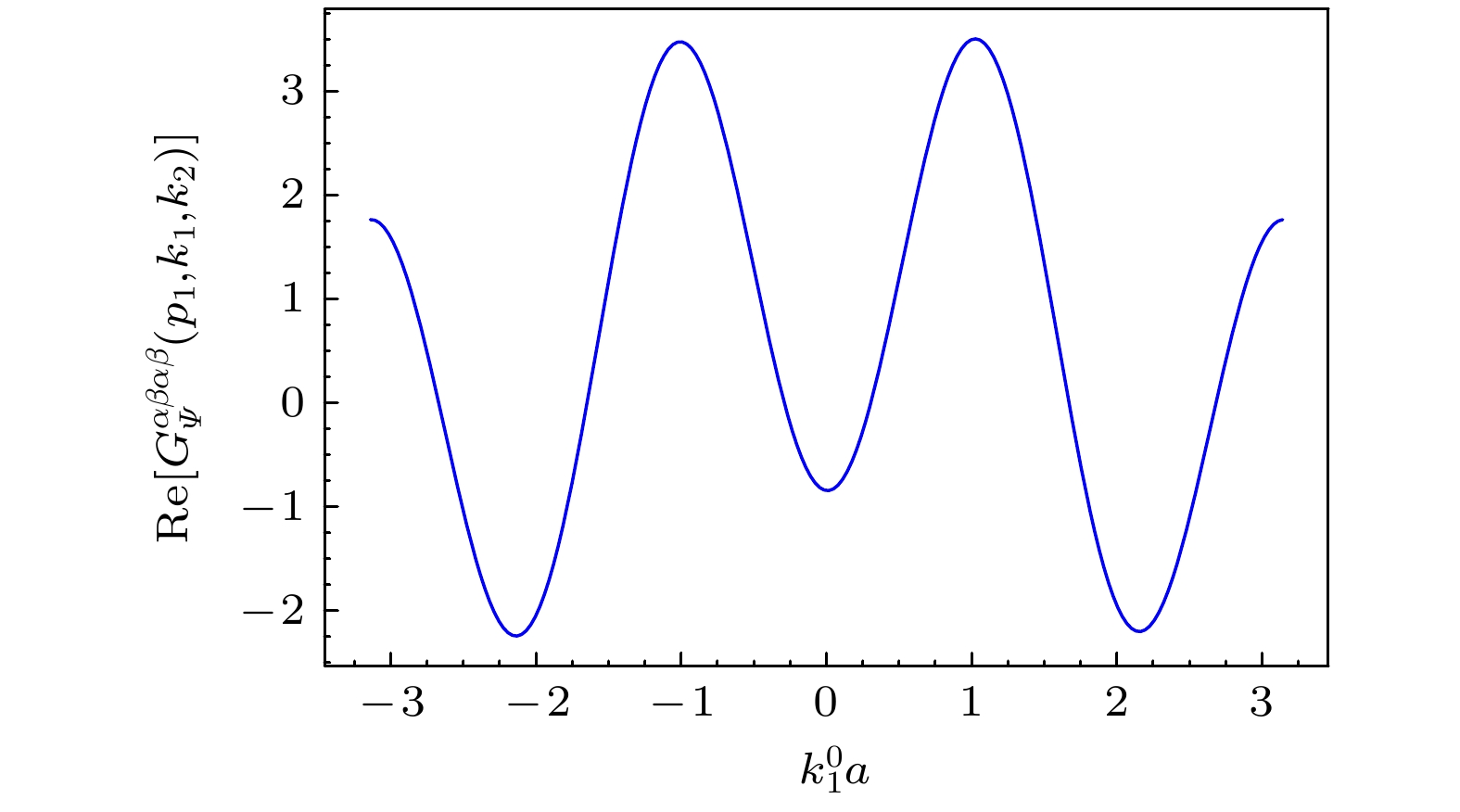
$ G^{\alpha\beta\alpha\beta}_\Psi(p_1, $ $ k_1, k_2) $ 的实部. 其中外腿动量选定为$ k_1=(k_1^0, 0), \, k_2=(0, $ $ \pi/a), \, p_1=(0, 0) $ Fig. 11. Real part of
$ G^{\alpha\beta\alpha\beta}_\Psi(p_1, k_1, k_2) $ in the 1+1-dimensional 1-flavor NJL model as a function of$ k_1^0 a $ , with$ k_1=(k_1^0, 0), \, k_2=(0, \pi/a), \, p_1=(0, 0) $ .
图 12 不同背景电场
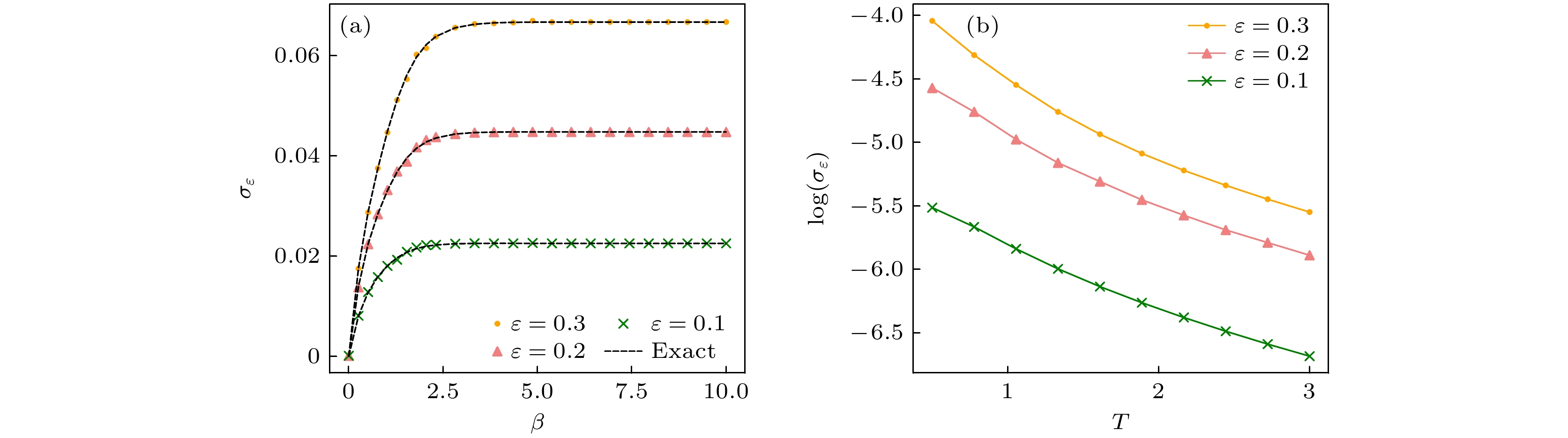
$ \varepsilon $ 下的弦张力. 其中给定$ m=1, \;g=1,\; \varpi=1 $ ,$ N $ = 6 (a) 弦张力对$ \beta $ 的依赖; (b) 弦张力的对数对温度$ T $ 的依赖Fig. 12. String tensions under different
$ \varepsilon $ in the case$ m=1,\; g=1, \;\varpi=1 $ ,$ N $ = 6: (a) The string tension as a function of the inverse temperature$ \beta $ ; (b) logarithm of the string tension as a function of the temperature$ T $ .
图 13 在给定参数
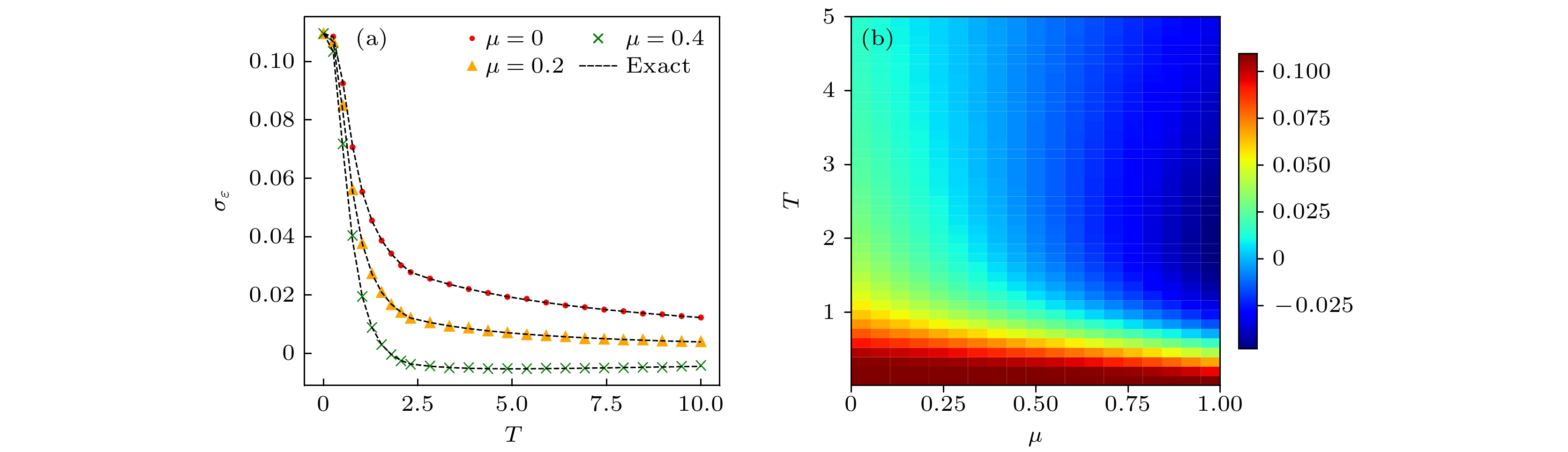
$ \varepsilon=0.5,\; m=1, \;g=1, \;\varpi=1,\; N=6 $ 下的弦张力 (a) 不同化学势 μ下弦张力对温度$ T $ 的依赖; (b) 弦张力对温度$ T $ 和化学势μ的依赖Fig. 13. The string tension in the case
$ \varepsilon=0.5,\; m=1,\; g=1,\; \varpi=1\;, N=6 $ : (a) At different μ, the string tension as a function of the temperature$ T $ ; (b) the string tension as a function of the temperature$ T $ and the chemical potential μ. -
[1] Alexandru A, Basar G, Bedaque P F, Vartak S, Warrington N C 2016 Phys. Rev. Lett. 117 081602
Google Scholar
[2] Troyer M, Wiese U J 2005 Phys. Rev. Lett. 94 170201
Google Scholar
[3] Feynman R P 1982 Int. J. Theor. Phys. 21 467
Google Scholar
[4] Jordan S P, Lee K S M, Preskill J 2012 Science 336 1130
Google Scholar
[5] Lamm H, Lawrence S, Yamauchi Y 2020 Phys. Rev. Res. 2 013272
Google Scholar
[6] Mueller N, Tarasov A, Venugopalan R 2020 Phys. Rev. D 102 016007
Google Scholar
[7] Echevarria M G, Egusquiza I L, Rico E, Schnell G 2021 Phys. Rev. D 104 014512
[8] Qian W, Basili R, Pal S, Luecke G, Vary J P 2022 Phys. Rev. Res. 4 043193
Google Scholar
[9] Li T, Guo X, Lai W K, Liu X, Wang E, Xing H, Zhang D B, Zhu S L 2022 Phys. Rev. D 10 5
[10] Li T, Guo X, Lai W K, Liu X, Wang E, Xing H, Zhang D B, Zhu S L 2023 Science China Physics, Mechanics & Astronomy 66 281011
[11] Bauer C W, de Jong W A, Nachman B, Provasoli D 2021 Phys. Rev. Lett. 126 062001
Google Scholar
[12] Bepari K, Malik S, Spannowsky M, Williams S 2022 Phys. Rev. D 106 056002
Google Scholar
[13] Hu Z, Xia R, Kais S 2020 Sci. Rep. 10 3301
Google Scholar
[14] De Jong W A, Metcalf M, Mulligan J, Płoskoń M, Ringer F, Yao X 2021 Phys. Rev. D 104 051501
[15] Yao X 2022 arXiv: 2205.07902 [High Energy Physics-Phenomenology
[16] Zhou Z Y, Su G X, Halimeh J C, Ott R, Sun H, Hauke P, Yang B, Yuan Z S, Berges J, Pan J W 2022 Science 377 abl6277
[17] de Jong W A, Lee K, Mulligan J, Płoskoń M, Ringer F, Yao X 2022 Phys. Rev. D 106 054508
[18] Briceño R A, Guerrero J V, Hansen M T, Sturzu A M 2021 Phys. Rev. D 103 014506
[19] Li T, Lai W K, Wang E, Xing H 2023 arXiv: 2301.04179 [High Energy Physics - Phenomenology
[20] Martinez E A, Muschik C A, Schindler M, et al. 2016 Nature 534 516
Google Scholar
[21] Atas Y Y, Haase J F, Zhang J, Wei V, Pfaendler S M L, Lewis R, Muschik C A 2022 arXiv: 2207.03473 [Quantum Physics
[22] Czajka A M, Kang Z B, Ma H, Zhao F 2022 JHEP 08 209
[23] Davoudi Z, Mueller N, Powers C 2022 arXiv: 2208.13112 [High Energy Physics - Lattice
[24] Tomiya A 2023 PoS LATTICE2022 039
[25] Czajka A M, Kang Z B, Tee Y, Zhao F 2022 arXiv: 2210.03062 [High Energy Physics - Phenomenology
[26] Xie X D, Guo X, Xing H, Xue Z Y, Zhang D B, Zhu S L 2022 Phys. Rev. D 106 054509
[27] McClean J R, Kimchi-Schwartz M E, Carter J, de Jong W A 2017 Phys. Rev. A 95 042308
Google Scholar
[28] Nakanishi K M, Mitarai K, Fujii K 2019 Phys. Rev. Res. 1 033062
Google Scholar
[29] Higgott O, Wang D, Brierley S 2019 Quantum 3 156
Google Scholar
[30] Zhang D B, Yuan Z H, Yin T 2020 arXiv: 2006.15781 [Quantum Physics
[31] Bärtschi A, Eidenbenz S 2019 In Gąsieniec L A, Jansson J, Levcopoulos C, editors, Fundamentals of Computation Theory (Cham: Springer International Publishing) pp126–139
[32] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [Quantum Physics
[33] Wiersema R, Zhou C, de Sereville Y, Carrasquilla J F, Kim Y B, Yuen H 2020 PRX Quantum 1 020319
Google Scholar
[34] Zhang D B, Zhang G Q, Xue Z Y, Zhu S L, Wang Z 2021 Phys. Rev. Lett 127 020502
Google Scholar
[35] Francis A, Zhu D, Huerta Alderete C, Johri S, Xiao X, Freericks J K, Monroe C, Linke N M, Kemper A F 2021 Sci. Adv. 7 eabf2447
Google Scholar
[36] Verdon G, Marks J, Nanda S, Leichenauer S, Hidary J 2019 arXiv: 1910.02071 [Quantum Physics
[37] Wu J, Hsieh T H 2019 Phys. Rev. Lett 123 220502
Google Scholar
[38] Zhu D, Johri S, Linke N M, Landsman K, Alderete C H, Nguyen N H, Matsuura A, Hsieh T, Monroe C 2020 Proc. Natl. Acad. Sci. 117 25402
Google Scholar
[39] Martyn J, Swingle B 2019 Phys. Rev. A 100 032107
Google Scholar
[40] Kliesch M, Gogolin C, Kastoryano M J, Riera A, Eisert J 2014 Phys. Rev. X 4 031019
[41] Pedernales J S, Di Candia R, Egusquiza I L, Casanova J, Solano E 2014 Phys. Rev. Lett. 113 020505
Google Scholar
[42] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge: Cambridge University Press) pp206–208
[43] Lin H W, Nocera E R, Olness F, et al. 2018 Prog. Part. Nucl. Phys. 100 107
Google Scholar
[44] Gao J, Harland-Lang L, Rojo J 2018 Phys. Rep. 742 1
Google Scholar
[45] Lepage G P, Brodsky S J 1980 Phys. Rev. D 22 2157
Google Scholar
[46] Efremov A V, Radyushkin A V 1980 Phys. Lett. B 94 245
Google Scholar
[47] Ji X 2013 Phys. Rev. Lett. 110 262002
Google Scholar
[48] Ji X 2014 Sci. China Phys. Mech. Astron. 57 1407
Google Scholar
[49] Ma Y Q, Qiu J W 2018 Phys. Rev. D 98 074021
Google Scholar
[50] Ma Y Q, Qiu J W 2018 Phys. Rev. Lett. 120 022003
Google Scholar
[51] Radyushkin A V 2017 Phys. Rev. D 96 034025
Google Scholar
[52] Orginos K, Radyushkin A, Karpie J, Zafeiropoulos S 2017 Phys. Rev. D 96 094503
[53] Liang J, Draper T, Liu K F, Rothkopf A, Yang Y B 2020 Phys. Rev. D 101 114503
Google Scholar
[54] Chambers A J, Horsley R, Nakamura Y, Perlt H, Rakow P E L, Schierholz G, Schiller A, Somfleth K, Young R D, Zanotti J M 2017 Phys. Rev. Lett. 118 242001
Google Scholar
[55] Sufian R S, Karpie J, Egerer C, Orginos K, Qiu J W, Richards D G 2019 Phys. Rev. D 99 074507
Google Scholar
[56] Izubuchi T, Jin L, Kallidonis C, Karthik N, Mukherjee S, Petreczky P, Shugert C, Syritsyn S 2019 Phys. Rev. D 100 034516
Google Scholar
[57] Lin H W, Chen J W, Fan Z, Zhang J H, Zhang R 2021 Phys. Rev. D 103 014516
[58] Musch B U, Hagler P, Engelhardt M, Negele J W, Schafer A 2012 Phys. Rev. D 85 094510
[59] Detmold W, Melnitchouk W, Negele J W, Renner D B, Thomas A W 2001 Phys. Rev. Lett. 87 172001
Google Scholar
[60] Hagler Ph, Schroers W, Bratt J, et al. 2008 Phys. Rev. D 77 094502
[61] Alexandrou C, Constantinou M, Dinter S, Drach V, Hadjiyiannakou K, Jansen K, Koutsou G, Vaquero A 2015 JHEP 06 068
[62] Alexandrou C, Bacchio S, Constantinou M, Finkenrath J, Hadjiyiannakou K, Jansen K, Koutsou G, Panagopoulos H, Spanoudes G 2020 Phys. Rev. D 101 094513
[63] Zhang J H, Chen J W, Ji X, Jin L, Lin H W 2017 Phys. Rev. D 95 094514
[64] Zhang J H, Jin L, Lin H W, Schäfer A, Sun P, Yang Y B, Zhang R, Zhao Y, Chen J W 2019 Nucl. Phys. B 939 429
Google Scholar
[65] Hua J, Chu M H, Sun P, Wang W, Xu J, Yang Y B, Zhang J H, Zhang Q A 2021 Phys. Rev. Lett. 127 062002
Google Scholar
[66] Hua J, Chu M H, He J C, et al. 2022 Phys. Rev. Lett. 129 132001
Google Scholar
[67] Luscher M 1986 Commun. Math. Phys. 105 153
Google Scholar
[68] Luscher M 1991 Nucl. Phys. B 354 531
Google Scholar
[69] Briceno R A, Dudek J J, Young R D 2018 Rev. Mod. Phys. 90 025001
Google Scholar
[70] Davoudi Z 2018 PoS LATTICE 2018 014
[71] Hansen M T, Sharpe S R 2019 Ann. Rev. Nucl. Part. Sci. 69 65
Google Scholar
[72] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 124 246
Google Scholar
[73] Nambu Y, Jona-Lasinio G 1961 Phys. Rev. 122 345
Google Scholar
[74] Gross D J, Neveu A 1974 Phys. Rev. D 10 3235
Google Scholar
[75] Backens S, Shnirman A, Makhlin Y 2019 Sci. Rep. 9 2
[76] Weinberg P, Bukov M 2017 SciPost Phys. 2 003
Google Scholar
[77] Steiger D S, Häner T, Troyer M 2018 Quantum 2 49
Google Scholar
[78] Collins J 2013 Foundations of Perturbative QCD (Cambridge: Cambridge University Press) pp174–176
[79] Ishikawa T, Jin L, Lin H W, Schäfer A, Yang Y B, Zhang J H, Zhao Y 2019 Sci. China Phys. Mech. Astron. 62 991021
Google Scholar
[80] Jia Y, Liang S, Xiong X, Yu R 2018 Phys. Rev. D 98 054011
Google Scholar
[81] Barry P C, Ji C R, Sato N, Melnitchouk W 2021 Phys. Rev. Lett. 127 232001
Google Scholar
[82] Chernyak V L, Zhitnitsky A R 1984 Phys. Rep. 112 173
Google Scholar
[83] Zhang R, Honkala C, Lin H W, Chen J W 2020 Phys. Rev. D 102 094519
[84] Jordan S P, Lee K S M, Preskill J 2014 Quant. Inf. Comput. 14 1014
[85] Jordan S P, Lee K S M, Preskill J 2014 arXiv: 1404.7115 [High Energy Physics-Theory
[86] Lehmann H, Symanzik H, Zimmerman W 1955 Nuovo Cimento 1 205
Google Scholar
[87] Abdalla E, Abdalla M C B, Rothe K D 1991 Non-perturbative Methods in 2D Quantum Field Theory (Singaproe: World Scientific Publishing House
[88] Lowenstein J, Swieca J 1971 Ann. Phys. 68 172
Google Scholar
[89] Byrnes T, Sriganesh P, Bursill R, Hamer C 2002 Phys. Rev. D 66 013002
Google Scholar
[90] Buyens B, Montangero S, Haegeman J, Verstraete F, Van Acoleyen K 2017 Phys. Rev. D 95 094509
[91] Zinn-Justin J 2002 In New Developments in Quantum Field Theory (Springer), pp217–232
[92] Kogut J, Susskind L 1975 Phys. Rev. D 11 395
[93] Fetter A L, Walecka J D 2012 Quantum Theory of Many-particle Systems (New York: Courier Corporation
[94] Casher A, Kogut J, Susskind L 1974 Phys. Rev. D 10 732
Google Scholar
[95] Hamer C, Kogut J, Crewther D, Mazzolini M 1982 Nucl. Phys. B 208 413
Google Scholar
[96] Buyens B, Verstraete F, Van Acoleyen K 2016 Phys. Rev. D 94 085018
Google Scholar
[97] Johansson J R, Nation P D, Nori F 2012 Comput. Phys. Commun. 183 1760
Google Scholar
[98] Pisarski R D, Alvarez O 1982 Phys. Rev. D 26 3735
Google Scholar
[99] Fodor Z, Katz S D 2004 J. High Energy Phys. 2004 050
[100] D’ Elia M, Lombardo M P 2003 Phys. Rev. D 67 014505
[101] Allton C R, Ejiri S, Hands S J, Kaczmarek O, Karsch F, Laermann E, Schmidt C 2003 Phys. Rev. D 68 014507
下载:
计量
- 文章访问数: 2863
- PDF下载量: 145
- 被引次数: 0
