强驱动单态-三重态量子比特的高保真单比特门

刘启沛; 张程贤; 薛正远

doi:10.7498/aps.72.20230906

摘要

半导体量子点量子比特是最有希望实现量子计算的候选者之一. 其中自旋单态-三重态量子比特因具有全电控制和读取准确的优良性质而备受关注. 为增强对电荷噪声的免疫, 通常引进强脉冲驱动以尽可能加快门操作速度. 但是, 强驱动脉冲引起的复杂动力学导致旋波近似不再适用, 反而会阻碍高保真度比特操作的实现. 本文提出了一种增加简单的正交脉冲的方法, 可以很好地抑制强驱动引起的高频振荡项的操作错误. 数值计算结果表明, NOT门的保真度在无噪声时可达99.99%且操作时间只需2 ns. 特别地, 即便电荷噪声强度到了$ 2\ \mu{\rm{eV}} $的水平, NOT门的平均保真度也可高于99.9%. 值得注意的是, 该方案同时也适用于任意单比特量子门的优化. 因此, 本文的脉冲优化方案将有助于获得快速高保真度的自旋单态-三重态量子比特.

关键词:

Abstract

Semiconductor quantum dot qubits are one of the most promising candidates for quantum computing. Among them, singlet-triplet qubits have attracted much attention due to their excellent properties of all-electric control and accurate readout. To improve qubit immunity to charge noise, strong driving pulses are usually introduced to make operation as fast as possible. However, the complex dynamics induced by strong driving pulses make the rotating wave approximation inapplicable and hinder the implementation of high-fidelity qubit operation. In this work, we present a method of utilizing simple quadrature pulses to correct errors of high-frequency oscillatory terms induced by strong driving. A scheme to obtain these pulses is proposed based on a full quantization of the system and derivative removal by adiabatic gate (DRAG) theory, as the former clarifies the elementary processes of strong driving effects and enables the latter to find correction pulse shapes. The numerical simulation results show that, a NOT gate with 99.99% fidelity and gate time as short as 2 ns can be achieved with the help of the control pulses of this method, which indicates that the control error brought by strong driving is no longer a limiting factor. In particular, NOT gate fidelity higher than 99.9% is achievable even when the charge noise is at a level of $ 2\ \mu{\rm{eV}} $. Notice that this method can be applied to any resonant-driving single-qubit rotation but not just NOT gates. Therefore, our approach will facilitate qubits to realize fast, high-fidelity single-qubit gates under charge noise.

Keywords:

作者及机构信息

1.
华南师范大学物理学院, 原子亚原子结构与量子调控教育部重点实验室, 广州　510006

2.
广西大学物理科学与工程技术学院, 南宁　530004

3.
华南师范大学物理前沿科学研究院, 广东省量子调控与量子材料重点实验室, 粤港量子物质实验室, 广州　510006

4.
合肥国家实验室, 合肥　230088

通信作者: 张程贤, cxzhang@gxu.edu.cn ; 薛正远, zyxue83@163.com

基金项目: 国家自然科学基金(批准号: 11905065, 12275090)、广西科技基地和人才专项(批准号: 桂科AD22035186)、广东省重点实验室(批准号: 2020B1212060066)和科技创新2030——“量子通信与量子计算机”重大项目(批准号: 2021ZD0302303)资助的课题.

Authors and contacts

1.
Key Laboratory of Atomic and Subatomic Structure and Quantum Control (Ministry of Education), School of Physics, South China Normal University, Guangzhou 510006, China

2.
School of Physical Science and Technology, Guangxi University, Nanning 530004, China

3.
Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, Guangdong-Hong Kong Joint Laboratory of Quantum Matter, Frontier Research Institute for Physics, South China Normal University, Guangzhou 510006, China

4.
Hefei National Laboratory, Hefei 230088, China

Corresponding author: Zhang Cheng-Xian, cxzhang@gxu.edu.cn ; Xue Zheng-Yuan, zyxue83@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11905065, 12275090), the Guangxi Science Foundation, China (Grant No. AD22035186), the Key Laboratory of Guangdong Province, China (Grant No. 2020B1212060066), and the Innovation Program for Quantum Science and Technology, China (Grant No. 2021ZD0302303).

文章全文 : translate this paragraph

参考文献

[1]	Chatterjee A, Stevenson P, De Franceschi S, Morello A, de Leon N, Kuemmeth F 2021 Nat. Rev. Phys. 3 157 Google Scholar
[2]	王保传, 陈明博, 曹刚, 郭国平 2018 物理 47 725 Google Scholar Wang B C, Chen M B, Cao G, Guo G P 2018 PHYSICS.47 725 Google Scholar
[3]	王宁, 王保传, 郭国平 2022 71 230301 Google Scholar Wang N, Wang B C, Guo G P 2022 Acta Phys. Sin. 71 230301 Google Scholar
[4]	Yoneda J, Takeda K, Otsuka T, et al. 2018 Nat. Nanotech. 13 102 Google Scholar
[5]	Takeda K, Kamioka J, Otsuka T, et al. 2016 Sci. Adv. 2 e1600694 Google Scholar
[6]	Veldhorst M, Hwang J C C, Yang C H, et al. 2014 Nat. Nanotech. 9 981 Google Scholar
[7]	Mills A R, Guinn C R, Gullans M J, Sigillito A J, Feldman M M, Nielsen E, Petta J R 2022 Sci. Adv. 8 eabn5130 Google Scholar
[8]	Xue X, Russ M, Samkharadze N, Undseth B, Sammak A, Scappucci G, Vandersypen L M K 2022 Nature 601 343 Google Scholar
[9]	Noiri A, Takeda K, Nakajima T, Kobayashi T, Sammak A, Scappucci G, Tarucha S 2022 Nature 601 338 Google Scholar
[10]	Loss D, DiVincenzo D P 1998 Phys. Rev. A 57 120 Google Scholar
[11]	Petta J R, Johnson A C, Taylor J M, et al. 2005 Science 309 2180 Google Scholar
[12]	DiVincenzo D P, Bacon D, Kempe J, Burkard G, Whaley K B 2000 Nature 408 339 Google Scholar
[13]	Friesen M, Ghosh J, Eriksson M A, Coppersmith S N 2017 Nat. Commun. 8 15923 Google Scholar
[14]	Wu X, Ward D R, Prance J R, et al. 2014 Proc. Natl. Acad. Sci. USA 111 11938 Google Scholar
[15]	Barthel C, Medford J, Bluhm H, Yacoby A, Marcus C M, Hanson M P, Gossard A C 2012 Phys. Rev. B 85 035306 Google Scholar
[16]	Borjans F, Mi X, Petta J R 2021 Phys. Rev. Appl. 15 044052 Google Scholar
[17]	Eng K, Ladd T D, Smith A, et al. 2015 Sci. Adv. 1 e1500214 Google Scholar
[18]	Andrews R W, Jones C, Reed M D, et al. 2019 Nat. Nanotech. 14 747 Google Scholar
[19]	Bermeister A, Keith D, Culcer D 2014 Appl. Phys. Lett. 105 192102 Google Scholar
[20]	Chan K W, Huang W, Yang C H, et al. 2018 Phys. Rev. Appl. 10 044017 Google Scholar
[21]	Martins F, Malinowski F K, Nissen P D, et al. 2016 Phys. Rev. Lett. 116 116801 Google Scholar
[22]	Reed M D, Maune B M, Andrews R W, et al. 2016 Phys. Rev. Lett. 116 110402 Google Scholar
[23]	Abadillo-Uriel J C, Eriksson M A, Coppersmith S N, Friesen M 2019 Nat. Commun. 10 5641 Google Scholar
[24]	Yang Y C, Coppersmith S N, Friesen M 2017 Phys. Rev. A 95 062321 Google Scholar
[25]	Takeda K, Noiri A, Yoneda J, Nakajima T, Tarucha S 2020 Phys. Rev. Lett. 124 117701 Google Scholar
[26]	Xie W X, Zhang C X, Xue Z Y 2021 Ann. Phys. 533 2100054 Google Scholar
[27]	Abadillo-Uriel, J C, King C, Coppersmith S N, Friesen M 2021 Phys. Rev. A 104 032612 Google Scholar
[28]	Zajac D M, Sigillito A J, Russ M, Borjans F, Taylor J M, Burkard G, Petta J R 2018 Science 359 439 Google Scholar
[29]	Bloch F, Siegert A 1940 Phys. Rev. 57 522 Google Scholar
[30]	Shirley J H 1965 Phys. Rev. 138 B979 Google Scholar
[31]	Cohen-Tannoudji C, Dupont-Roc J, Fabre C 1973 J. Phys. B 6 L214 Google Scholar
[32]	Gambetta J M, Motzoi F, Merkel S T, Wilhelm F K 2011 Phys. Rev. A 83 012308 Google Scholar
[33]	Motzoi F, Wilhelm F K 2013 Phys. Rev. A 88 062318 Google Scholar
[34]	Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (10th Anniversary Ed.) (Cambridge: Cambridge University Press) pp174–177
[35]	Yoneda J, Otsuka T, Takakura T, et al. 2015 Appl. Phys. Exp. 8 084401 Google Scholar
[36]	Nielsen M A 2002 Phys. Lett. A 303 249 Google Scholar
[37]	Elman S J, Bartlett S D, Doherty A C 2017 Phys. Rev. B 96 115407 Google Scholar
[38]	Mi X, Kohler S, Petta J R 2018 Phys. Rev. B 98 161404(R Google Scholar
[39]	Petersson K D, Petta J R, Lu H, Gossard A C 2010 Phys. Rev. Lett. 105 246804 Google Scholar
[40]	Nichol J M, Orona L A, Harvey S P, Fallahi S, Gardner G C, Manfra M J, Yacoby A 2017 npj Quantum Inf. 3 3 Google Scholar

施引文献

图 1 全量子化哈密顿量的裸态能级图

Fig. 1. Energy levels of the full quantized Hamiltonian for the bare states.

下载: 全尺寸图片幻灯片

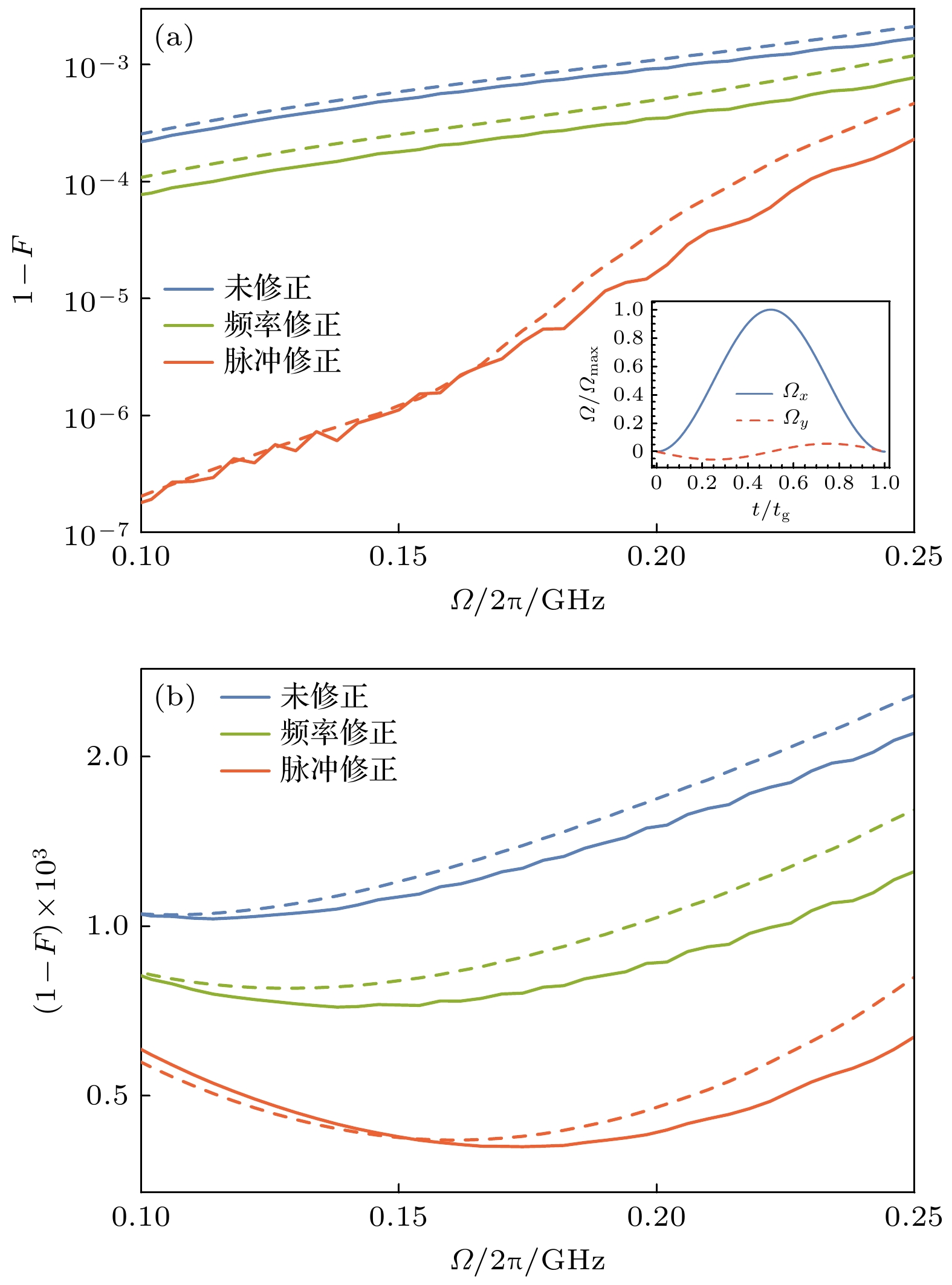
图 2 (a)无噪声时和(b)电荷噪声下的NOT门表现. 频率修正和脉冲修正分别指文献[24]和本文所用的修正方案. 实线和虚线分别对应$\varOmega_x$脉冲的包络为高斯型和三角函数型. 图(a)右下角的插入图为高斯型$\varOmega_x$及其对应的$\varOmega_y$的示意图. 所用参数为$V_{01}=0.6402$, $V_{0 {\rm{f}}}=0.5309$, V_1f = 0.0014

Fig. 2. NOT gate performance under (a) noise-free and (b) charge noise. The frequency correction and the pulse correction refers to the correction scheme used in Ref. [24] and this work, respectively. The Gaussian and trigonometric $\varOmega_x$ pulse envelopes are represented by the solid and dashed lines, respectively. The bottem right insert in panel (a) is a diagram of Gaussian $\varOmega_x$ and its corresponding $\varOmega_y$. Parameters: $ V_ {01} = 0.6402 $, $ V_ {0 {\rm{f}}} = 0.5309 $, $ V_ {1 {\rm{f}}} = 0.0014 $.

下载: 全尺寸图片幻灯片

map

[1]	Chatterjee A, Stevenson P, De Franceschi S, Morello A, de Leon N, Kuemmeth F 2021 Nat. Rev. Phys. 3 157 Google Scholar
[2]	王保传, 陈明博, 曹刚, 郭国平 2018 物理 47 725 Google Scholar Wang B C, Chen M B, Cao G, Guo G P 2018 PHYSICS.47 725 Google Scholar
[3]	王宁, 王保传, 郭国平 2022 71 230301 Google Scholar Wang N, Wang B C, Guo G P 2022 Acta Phys. Sin. 71 230301 Google Scholar
[4]	Yoneda J, Takeda K, Otsuka T, et al. 2018 Nat. Nanotech. 13 102 Google Scholar
[5]	Takeda K, Kamioka J, Otsuka T, et al. 2016 Sci. Adv. 2 e1600694 Google Scholar
[6]	Veldhorst M, Hwang J C C, Yang C H, et al. 2014 Nat. Nanotech. 9 981 Google Scholar
[7]	Mills A R, Guinn C R, Gullans M J, Sigillito A J, Feldman M M, Nielsen E, Petta J R 2022 Sci. Adv. 8 eabn5130 Google Scholar
[8]	Xue X, Russ M, Samkharadze N, Undseth B, Sammak A, Scappucci G, Vandersypen L M K 2022 Nature 601 343 Google Scholar
[9]	Noiri A, Takeda K, Nakajima T, Kobayashi T, Sammak A, Scappucci G, Tarucha S 2022 Nature 601 338 Google Scholar
[10]	Loss D, DiVincenzo D P 1998 Phys. Rev. A 57 120 Google Scholar
[11]	Petta J R, Johnson A C, Taylor J M, et al. 2005 Science 309 2180 Google Scholar
[12]	DiVincenzo D P, Bacon D, Kempe J, Burkard G, Whaley K B 2000 Nature 408 339 Google Scholar
[13]	Friesen M, Ghosh J, Eriksson M A, Coppersmith S N 2017 Nat. Commun. 8 15923 Google Scholar
[14]	Wu X, Ward D R, Prance J R, et al. 2014 Proc. Natl. Acad. Sci. USA 111 11938 Google Scholar
[15]	Barthel C, Medford J, Bluhm H, Yacoby A, Marcus C M, Hanson M P, Gossard A C 2012 Phys. Rev. B 85 035306 Google Scholar
[16]	Borjans F, Mi X, Petta J R 2021 Phys. Rev. Appl. 15 044052 Google Scholar
[17]	Eng K, Ladd T D, Smith A, et al. 2015 Sci. Adv. 1 e1500214 Google Scholar
[18]	Andrews R W, Jones C, Reed M D, et al. 2019 Nat. Nanotech. 14 747 Google Scholar
[19]	Bermeister A, Keith D, Culcer D 2014 Appl. Phys. Lett. 105 192102 Google Scholar
[20]	Chan K W, Huang W, Yang C H, et al. 2018 Phys. Rev. Appl. 10 044017 Google Scholar
[21]	Martins F, Malinowski F K, Nissen P D, et al. 2016 Phys. Rev. Lett. 116 116801 Google Scholar
[22]	Reed M D, Maune B M, Andrews R W, et al. 2016 Phys. Rev. Lett. 116 110402 Google Scholar
[23]	Abadillo-Uriel J C, Eriksson M A, Coppersmith S N, Friesen M 2019 Nat. Commun. 10 5641 Google Scholar
[24]	Yang Y C, Coppersmith S N, Friesen M 2017 Phys. Rev. A 95 062321 Google Scholar
[25]	Takeda K, Noiri A, Yoneda J, Nakajima T, Tarucha S 2020 Phys. Rev. Lett. 124 117701 Google Scholar
[26]	Xie W X, Zhang C X, Xue Z Y 2021 Ann. Phys. 533 2100054 Google Scholar
[27]	Abadillo-Uriel, J C, King C, Coppersmith S N, Friesen M 2021 Phys. Rev. A 104 032612 Google Scholar
[28]	Zajac D M, Sigillito A J, Russ M, Borjans F, Taylor J M, Burkard G, Petta J R 2018 Science 359 439 Google Scholar
[29]	Bloch F, Siegert A 1940 Phys. Rev. 57 522 Google Scholar
[30]	Shirley J H 1965 Phys. Rev. 138 B979 Google Scholar
[31]	Cohen-Tannoudji C, Dupont-Roc J, Fabre C 1973 J. Phys. B 6 L214 Google Scholar
[32]	Gambetta J M, Motzoi F, Merkel S T, Wilhelm F K 2011 Phys. Rev. A 83 012308 Google Scholar
[33]	Motzoi F, Wilhelm F K 2013 Phys. Rev. A 88 062318 Google Scholar
[34]	Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (10th Anniversary Ed.) (Cambridge: Cambridge University Press) pp174–177
[35]	Yoneda J, Otsuka T, Takakura T, et al. 2015 Appl. Phys. Exp. 8 084401 Google Scholar
[36]	Nielsen M A 2002 Phys. Lett. A 303 249 Google Scholar
[37]	Elman S J, Bartlett S D, Doherty A C 2017 Phys. Rev. B 96 115407 Google Scholar
[38]	Mi X, Kohler S, Petta J R 2018 Phys. Rev. B 98 161404(R Google Scholar
[39]	Petersson K D, Petta J R, Lu H, Gossard A C 2010 Phys. Rev. Lett. 105 246804 Google Scholar
[40]	Nichol J M, Orona L A, Harvey S P, Fallahi S, Gardner G C, Manfra M J, Yacoby A 2017 npj Quantum Inf. 3 3 Google Scholar

[1]	王粲, 陆朝阳, 陈明城. 时间旅行的量子门. , 2024, 73(2): 020303. doi: 10.7498/aps.73.20231289
[2]	赵艳军, 谭宁, 王堉琪, 郑亚锐, 王辉, 刘伍明. 规范势下正方形格点超导量子比特电路中的量子态输运. , 2023, 72(10): 100304. doi: 10.7498/aps.72.20222349
[3]	李岩, 任志红. 多量子比特WV纠缠态在Lipkin-Meshkov-Glick模型下的量子Fisher信息. , 2023, 72(22): 220302. doi: 10.7498/aps.72.20231179
[4]	熊凡, 陈永聪, 敖平. 热噪声环境下偶极场驱动的量子比特动力学. , 2023, 72(17): 170302. doi: 10.7498/aps.72.20230625
[5]	胡强, 曾柏云, 辜鹏宇, 贾欣燕, 樊代和. 退相干条件下两比特纠缠态的量子非局域关联检验. , 2022, 71(7): 070301. doi: 10.7498/aps.71.20211453
[6]	徐达, 王逸璞, 李铁夫, 游建强. 微波驱动下超导量子比特与磁振子的相干耦合. , 2022, 71(15): 150302. doi: 10.7498/aps.71.20220260
[7]	丁晨, 李坦, 张硕, 郭楚, 黄合良, 鲍皖苏. 基于辅助单比特测量的量子态读取算法. , 2021, 70(21): 210303. doi: 10.7498/aps.70.20211066
[8]	汪野, 张静宁, 金奇奂. 相干时间超过10 min的单离子量子比特. , 2019, 68(3): 030306. doi: 10.7498/aps.68.20181729
[9]	于宛让, 计新. 基于超绝热捷径技术快速制备超导三量子比特Greenberger-Horne-Zeilinger态. , 2019, 68(3): 030302. doi: 10.7498/aps.68.20181922
[10]	黄江. 弱测量对四个量子比特量子态的保护. , 2017, 66(1): 010301. doi: 10.7498/aps.66.010301
[11]	赵娜, 刘建设, 李铁夫, 陈炜. 超导量子比特的耦合研究进展. , 2013, 62(1): 010301. doi: 10.7498/aps.62.010301
[12]	高峰, 王叶兵, 田晓, 许朋, 常宏. 锶原子三重态谱线的观测及在光钟中的应用. , 2012, 61(17): 173201. doi: 10.7498/aps.61.173201
[13]	乔盼盼, 艾合买提·阿不力孜, 蔡江涛, 路俊哲, 麦麦提依明·吐孙, 日比古·买买提明. 利用热平衡态超导电荷量子比特实现量子隐形传态. , 2012, 61(24): 240303. doi: 10.7498/aps.61.240303
[14]	吴世海, 胡明亮, 李季, 惠小强. 用约瑟夫森电荷比特系统实现一种特殊量子态的传输. , 2011, 60(1): 010302. doi: 10.7498/aps.60.010302
[15]	张国锋, 邢钊. 基于非均匀外场的双量子比特自旋XYZ模型的swap门操作. , 2010, 59(3): 1468-1472. doi: 10.7498/aps.59.1468
[16]	孙震, 安忠, 李元, 刘文, 刘德胜, 解士杰. 高聚物中极化子和三重态激子的碰撞过程研究. , 2009, 58(6): 4150-4155. doi: 10.7498/aps.58.4150
[17]	高宽云, 赵翠兰. 量子环中量子比特的性质. , 2008, 57(7): 4446-4449. doi: 10.7498/aps.57.4446
[18]	刘承师, 马本堃. 在强交变电场驱动下线形三量子点分子中激子的动态局域化行为. , 2003, 52(8): 2027-2032. doi: 10.7498/aps.52.2027
[19]	厉彦民, 章立源. 三重态双极化子系统的超导与铁磁共存. , 1987, 36(2): 157-164. doi: 10.7498/aps.36.157
[20]	厉彦民, 章立源. 三重态双极化子的超导A相与B相. , 1986, 35(12): 1616-1623. doi: 10.7498/aps.35.1616

计量

文章访问数: 2614
PDF下载量: 83
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

强驱动单态-三重态量子比特的高保真单比特门