-
传播子在路径积分理论中扮演着核心角色, 因此在路径积分理论可使用的多个现代量子物理领域中有重要价值. 然而, 由于其一直未能在实验中被直接测量, 基于路径积分表述研究量子系统的实验进展受到了严重制约. 最近, 基于波函数直接测量方法, 我们提出了传播子测量方案, 并利用单光子实验首次成功实现了传播子的实验测量. 此外, 在这项研究中还首次演示了量子力学的最小作用量原理. 该研究成功解决了路径积分实验研究中的技术难题. 本文综述了此领域的研究进展, 具体为简述波函数直接测量的基本概念和研究进展, 并详细介绍传播子测量的理论模型、实验设计和实验结果. 最后, 介绍了一个重要的应用范例, 即通过传播子测量实现最小作用量原理的实验演示. 本文综述的传播子测量研究进展, 将为今后使用该方法开展相关实验研究提供重要的参考.The propagator plays a central role in path integral theory and therefore has significant value in various fields of modern quantum physics, where path integral representations can be used. However, owing to the fact that it has not been directly measured in experiment, progress of experimental studies of quantum systems based on path integral representations has been seriously limited. Recently, we proposed a propagator measurement scheme based on the direct measurement of the wave function and successfully performed the first experimental measurement of the propagator by using a single photon experiment. Furthermore, in this study, the quantum principle of least action is demonstrated for the first time. This research successfully addresses the technical challenges of path integral experimental studies. In this work, we review the research progress in this field, including a brief introduction to the basic concepts and research progress of direct wave function measurement, and a detailed description of the theoretical model, experimental design, and experimental results of propagator measurement. Finally, we introduce an important application example, which can serve as the experimental demonstration of the quantum principle of least action through propagator measurement. The research progress of propagator measurement reviewed in this work will provide important references for future experimental studies by using this method.
-
Keywords:
- quantum measurement /
- propagator /
- path integrals /
- quantum principle of least action
[1] Feynman R P 1948 Rev. Mod. Phys. 20 367
Google Scholar
[2] Feynman R P 2005 Feynman’s Thesis—A New Approach to Quantum Theory (Singapore: World Scientific Publishing Co Pte Ltd) pp1–69
[3] Feynman R P, Hibbs A R, Styer D F 2010 Quantum Mechanics and Path Integrals (Chelmsford: Courier Corporation) pp1–384
[4] Wen Y L, Wang Y F, Tian L M, Zhang S C, Li J F, Du J S, Yan H, Zhu S L 2023 Nat. Photonics 17 717
Google Scholar
[5] Von Neumann J 2018 Mathematical Foundations of Quantum Mechanics (New Edition) (Princeton: Princeton university press) pp271–288
[6] Aharonov Y, Albert D Z, Vaidman L 1988 Phys. Rev. Lett. 60 1351
Google Scholar
[7] Lundeen J S, Sutherland B, Patel A, Stewart C, Bamber C 2011 Nature 474 188
Google Scholar
[8] Hofheinz M, Wang H, Ansmann M, Bialczak R C, Lucero E, Neeley M, O’Connell A D, Sank D, Wenner J, MartinisJ M, ClelandA N 2009 Nature 459 546
Google Scholar
[9] Cramer M, Plenio M B, Flammia S T, Somma R, Gross D, Bartlett S D, Landon-Cardinal O, Poulin D, Liu Y K 2010 Nat. Commun. 1 149
Google Scholar
[10] Ritchie N W M, Story J G, Hulet R G 1991 Phys. Rev. Lett. 66 1107
Google Scholar
[11] Hosten O, Kwiat P 2008 Science 319 787
Google Scholar
[12] Starling D J, Dixon P B, Jordan A N, Howell J C 2009 Phys. Rev. A 80 041803
Google Scholar
[13] Zhou L, Turek Y, Sun C P, Nori F 2013 Phys. Rev. A 88 053815
Google Scholar
[14] Zhou X X, Xiao Z C, Luo H L, Wen S C 2012 Phys. Rev. A 85 043809
Google Scholar
[15] Rodenburg B, Mirhosseini M, Magaña-Loaiza O S, Boyd R W 2014 JOSA B 3 1
Google Scholar
[16] Magaña-Loaiza O S, Mirhosseini M, Rodenburg B, Boyd R W 2014 Phys. Rev. Lett. 112 200401
Google Scholar
[17] Starling D J, Dixon P B, Williams N S, Jordan A N, Howell J C 2010 Phys. Rev. A 82 011802
Google Scholar
[18] Xu X Y, Kedem Y, Sun K, Vaidman L, Li C F, Guo G C 2013 Phys. Rev. Lett. 111 033604
Google Scholar
[19] Starling D J, Dixon P B, Jordan A N, Howell J C 2010 Phys. Rev. A 82 063822
Google Scholar
[20] Brunner N, Simon C 2010 Phys. Rev. Lett. 105 010405
Google Scholar
[21] Strübi G, Bruder C 2013 Phys. Rev. Lett. 110 083605
Google Scholar
[22] Hallaji M, Feizpour A, Dmochowski G, Sinclair J, Steinberg A M 2017 Nat. Phys. 13 540
Google Scholar
[23] Du S J, Peng Y G, Feng H R, Han F, Yang L W, Zheng Y J 2020 Chin. Phys. B 29 074202
Google Scholar
[24] Zhang C Y, Fang M F 2021 Chin. Phys. B 30 010303
Google Scholar
[25] Dressel J, Malik M, Miatto F M, Jordan A N, Boyd R W 2014 Rev. Mod. Phys. 86 307
Google Scholar
[26] Pfeifer M, Fischer P 2011 Opt. Express 19 16508
Google Scholar
[27] Qiu J D, Li Z X, Xie L G, Luo L, He Y, Ren C L, Zhang Z Y, Du J L 2021 Chin. Phys. B 30 064216
Google Scholar
[28] Fang S Z, Dai Y, Jiang Q W, Tan H T, Li G X, Wu Q L 2021 Chin. Phys. B 30 060601
Google Scholar
[29] Lundeen J S, Resch K J 2005 Phys. Lett. A 334 337
Google Scholar
[30] Salvail J Z, Agnew M, Johnson A S, Bolduc E, Leach J, Boyd R W 2013 Nat. Photonics 7 316
Google Scholar
[31] Malik M, Mirhosseini M, Lavery M P J, Leach J, Padgett M J, Boyd R W 2014 Nat. Commun. 5 3115
Google Scholar
[32] Thekkadath G S, Giner L, Chalich Y, Horton M J, Banker J, Lundeen J S 2016 Phys. Rev. Lett. 117 120401
Google Scholar
[33] Xiao Y, Kedem Y, Xu J S, Li C F, Guo G C 2017 Opt. Express 25 14463
Google Scholar
[34] Xiao Y, Wiseman H M, Xu J S, Kedem Y, Li C F, Guo G C 2019 Sci. Adv. 5 eaav9547
Google Scholar
[35] Cohen E, Pollak E 2018 Phys. Rev. A 98 042112
Google Scholar
[36] Bolduc E, Gariepy G, Leach J 2016 Nat. Commun. 7 10439
Google Scholar
[37] Pan W W, Xu X Y, Kedem Y, Wang Q Q, Chen Z, Jan M, Sun K, Xu J S, Han Y J, Li C F, Guo G C 2019 Phys. Rev. Lett. 123 150402
Google Scholar
[38] Chen M C, Li Y, Liu R Z, Wu D, Su Z E, Wang X L, Li L, Liu N L, Lu C Y, Pan J W 2021 Phys. Rev. Lett. 127 030402
Google Scholar
[39] Kobayashi H, Tamate S, Nakanishi T, Sugiyama K, Kitano M 2010 Phys. Rev. A 81 012104
Google Scholar
[40] Shi Z M, Mirhosseini M, Margiewicz J, Malik M, Rivera F, Zhu Z Y, Boyd R W 2015 Optica 2 388
Google Scholar
[41] Maccone L, Rusconi C C 2014 Phys. Rev. A 89 022122
Google Scholar
[42] Mirhosseini M, Magaña-Loaiza O S, Hashemi Rafsanjani S M, Boyd R W 2014 Phys. Rev. Lett. 113 090402
Google Scholar
[43] Xu L, Xu H C, Jiang T, Xu F X, Zheng K M, Wang B, Zhang A N, Zhang L J 2021 Phys. Rev. Lett. 127 180401
Google Scholar
[44] Piacentini F, Avella A, Levi M P, Gramegna M, Brida G, Degiovanni I P, Cohen E, Lussana R, Villa F, Tosi A, Zappa F, Genovese M 2016 Phys. Rev. Lett. 117 170402
Google Scholar
[45] Shojaee E, Jackson C S, Riofrío C A, Kalev A, Deutsch I H 2018 Phys. Rev. Lett. 112 130404
Google Scholar
[46] Bamber C, Lundeen J S 2014 Phys. Rev. Lett. 112 070405
Google Scholar
[47] Wu S J 2013 Sci. Rep. 3 1193
Google Scholar
[48] Kocsis S, Braverman B, Ravets S, Stevens M J, Mirin R P, Shalm L K, Steinberg A M 2011 Science 332 1170
Google Scholar
[49] Wen Y L, Zhang S C, Yan H, Zhu S L 2022 Chin. Phys. B 31 034206
Google Scholar
[50] 温永立, 张善超, 颜辉, 朱诗亮 2021 70 110301
Google Scholar
Wen Y L, Zhang S C, Yan H, Zhu S L 2021 Acta Phys. Sin. 70 110301
Google Scholar
[51] Romito A, Gefen Y 2014 Phys. Rev. B 90 085417
Google Scholar
[52] Vallone G, Dequal D 2016 Phys. Rev. Lett. 116 040502
Google Scholar
[53] Zhang S C, Zhou Y R, Mei Y F, Liao K Y, Wen Y L, Li J F, Zhang X D, Du S W, Yan H, Zhu S L 2019 Phys. Rev. Lett. 123 190402
Google Scholar
[54] Zhang C R, Hu M J, Hou Z B, Tang J F, Zhu J, Xiang G Y, Li C F, Guo G C, Zhang Y S 2020 Phys. Rev. A 101 012119
Google Scholar
[55] Zhang C R, Hu M J, Xiang G Y, Zhang Y S, Li C F, Guo G C 2020 Chin. Phys. Lett. 37 080301
Google Scholar
[56] Zhou Y Y, Zhao J, Hay D, McGonagle K, Boyd R W, Shi Z M 2021 Phys. Rev. Lett. 127 040402
Google Scholar
[57] Yang M, Xiao Y, Liao Y W, Liu Z H, Xu X Y, Xu J S, Li C F, Guo G C 2020 Laser Photonics Rev. 14 1900251
Google Scholar
[58] Calderaro L, Foletto G, Dequal D, Villoresi P, Vallone G 2018 Phys. Rev. Lett. 121 230501
Google Scholar
[59] Knarr S H, Lum D J, Schneeloch J, Howell J C 2018 Phys. Rev. A 98 023854
Google Scholar
[60] Pan Y M, Zhang J, Cohen E, Wu C W, Chen P X, Davidson N 2020 Nat. Phys. 16 1206
Google Scholar
[61] Rojo A, Bloch A 2018 The Principle of Least Action: History and Physics (Cambridg: Cambridge University Press) pp1–266
[62] 朱诗亮, 温永立, 颜辉 2023 物理 52 502
Google Scholar
Zhu S L, Wen Y L, Yan H 2023 Physics 52 502
Google Scholar
[63] Salières P, Carré B, Le Déroff L, Grasbon F, Paulus G G, Walther H, Kopold R, Becker W, Milosevic D B, Sanpera A, Lewenstein M 2001 Science 292 902
Google Scholar
[64] Gibbons G W, Hawking S W, Perry M J 1978 Nucl. Phys. B 138 141
Google Scholar
[65] Fujikawa K 1979 Phys. Rev. Lett. 42 1195
Google Scholar
[66] Ord G N, Gualtieri J A 2002 Phys. Rev. Lett. 89 250403
Google Scholar
[67] Caldeira A O, Leggett A J 1983 Physica A 121 587
Google Scholar
[68] Mühlbacher L, Rabani E 2008 Phys. Rev. Lett. 100 176403
Google Scholar
[69] Pollock E L, Ceperley D M 1984 Phys. Rev. B 30 2555
Google Scholar
[70] Reisenberger M P, Rovelli C 1997 Phys. Rev. D 56 3490
Google Scholar
[71] Hartle J B, Hawking S W 1983 Phys. Rev. D 28 2960
Google Scholar
[72] Ashtekar A, Campiglia M, Henderson A 2010 Phys. Rev. D 82 124043
Google Scholar
[73] Fujikawa K 1982 Phys. Rev. D 25 2584
Google Scholar
[74] Hartle J B, Hawking S W 1976 Phys. Rev. D 13 2188
Google Scholar
-
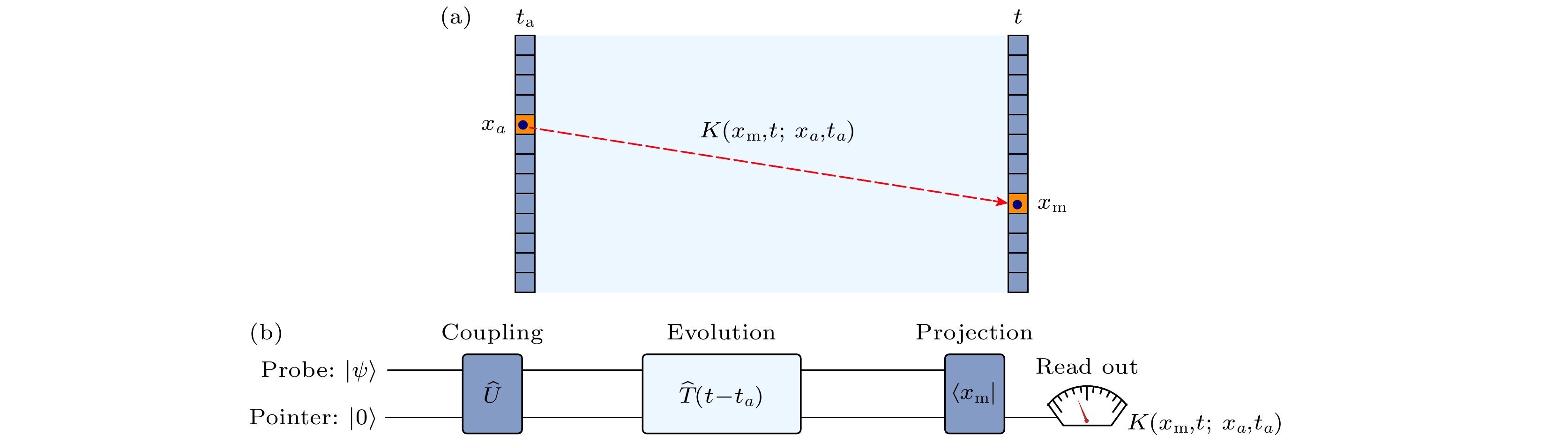
图 1 路径积分示意图及测量方法 (a) 传播子, 粒子从
$ (x_a, t_a) $ 传播到$ (x_{\rm{m}}, t) $ ; (b) 测量传播子的量子线路. 为了测量$ K(x_{\rm{m}}, t; $ $ x_a, t_a) $ , 首先需要制备量子态$ |\psi\rangle $ 和指针$ |0\rangle $ . 然后, 在$ t_a $ 时刻, 耦合操作$ {\hat{U}} $ 将系统的位置波函数与指针进行耦合. 演化之后, 将系统投影到t时刻的位置$ x_{\rm{m}} $ 上, 从指针读出$ K(x_{\rm{m}}, t;x_a, t_a) $ Fig. 1. Path integration diagram and measurement method: (a) Propagators: the propagation from
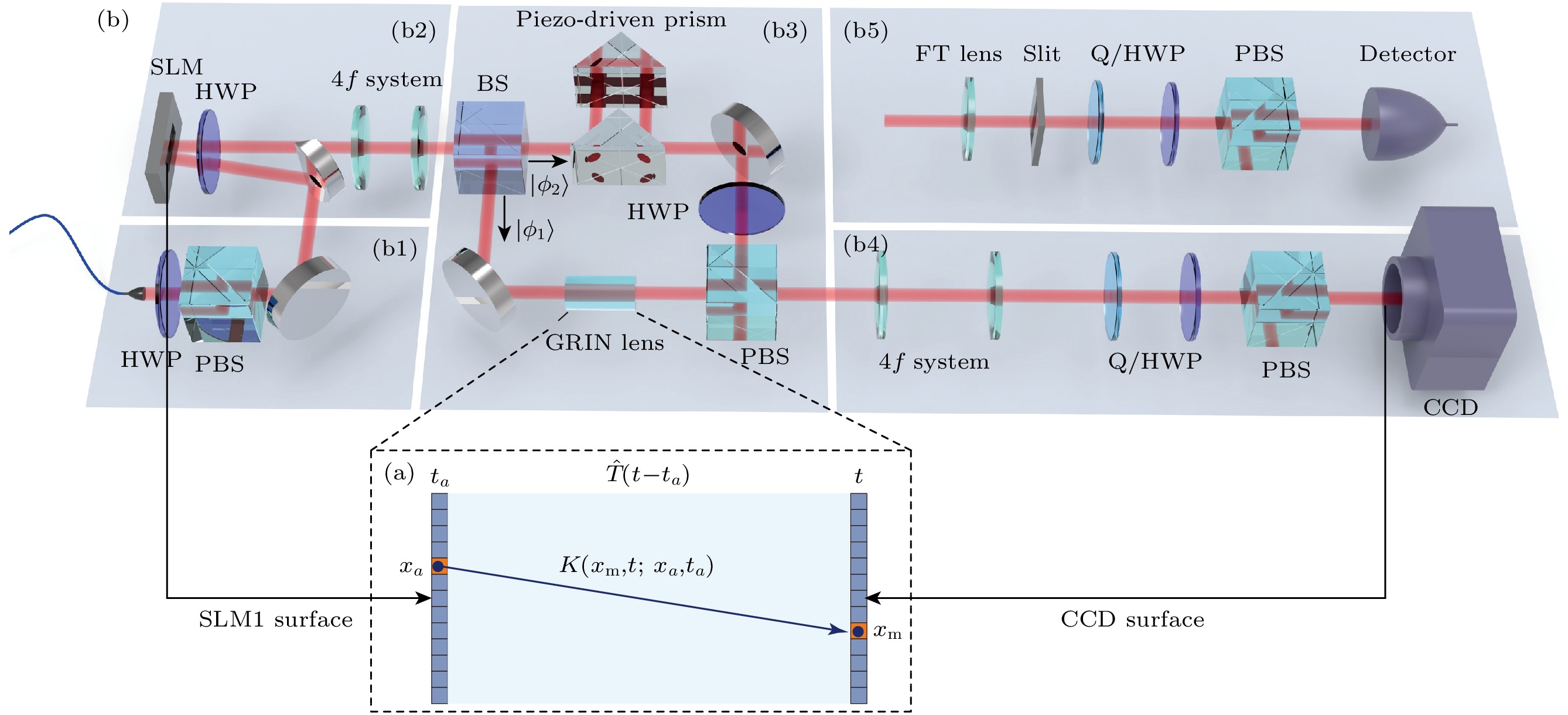
$ (x_a, t_a) $ to$ (x_{\rm{m}}, t) $ ; (b) protocol to measure the propagators. To measure$ K(x_{\rm{m}}, t;x_a, t_a) $ , the quantum state$ |\psi\rangle $ and pointer$ |0\rangle $ are prepared first. Then, at time$ t_a $ , a coupling operation$ {\hat{U}} $ couples the positional wave function of the probe system with the pointer. After the evolution, the system is projected to position$ x_{\rm{m}} $ at t, and$ K(x_{\rm{m}}, t;x_a, t_a) $ can be read out from the pointer
图 2 实验示意图 (a)演化和探测区域; (b1)初态制备; (b2)系统位置波函数与指针耦合; (b3)态的演化; (b4)位置的后选择与指针的读出; (b5)波函数的测量
Fig. 2. Schematic diagram of the experiment: (a) The evolution and detection region; (b1) initial state preparation; (b2) coupling of wave function and pointer; (b3) state evolution; (b4) post-selection of position and the readout of the pointer; (b5) measurement of the wave function
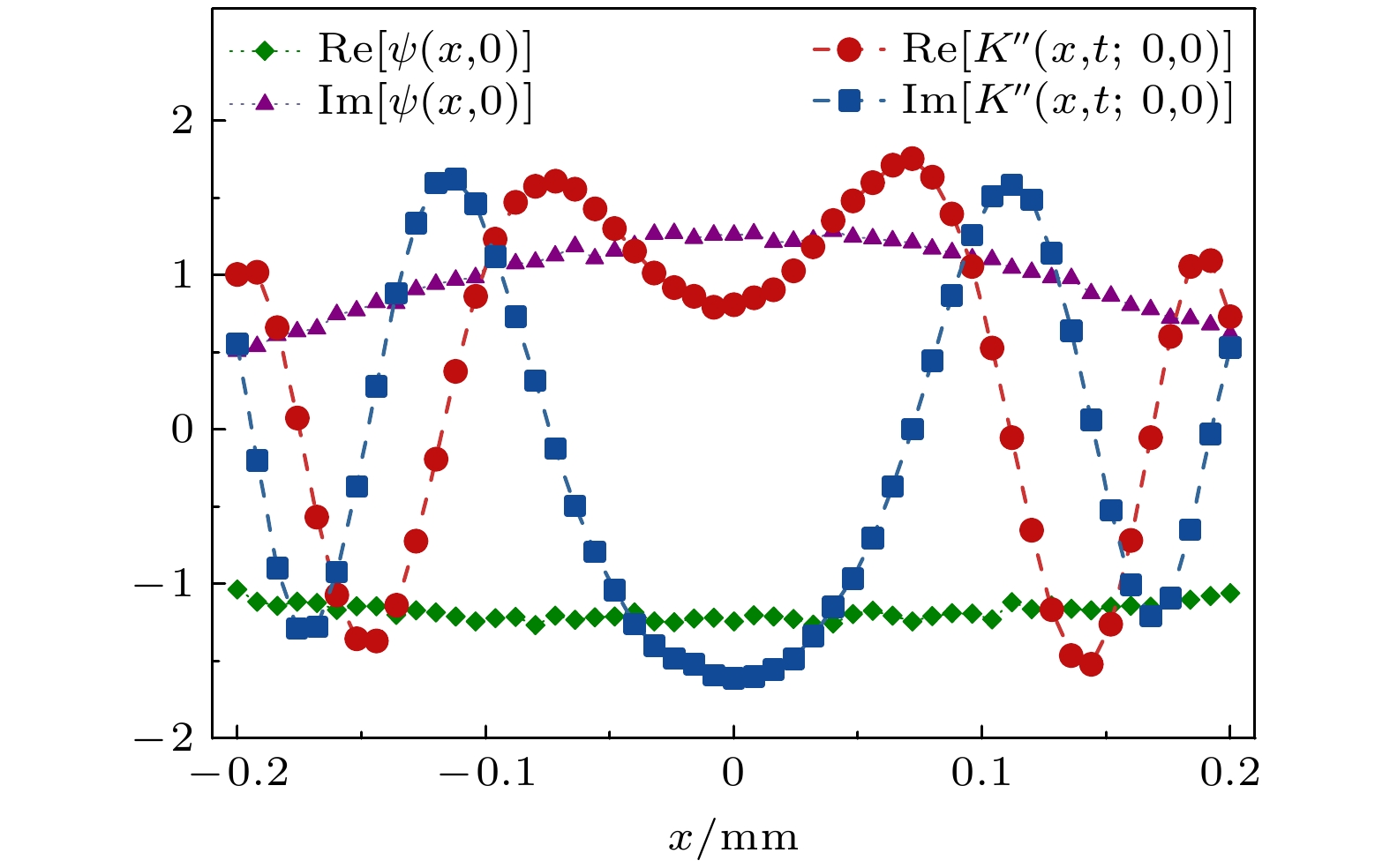
图 3
$ t=20 $ mm/c (c为真空中的光速)的$ K^{\prime\prime}(x, t;0, 0) $ 和波函数$ \psi(x, 0) $ 的实验测量结果. 蓝色方块和红色圆点分别展示了$ K^{\prime\prime}(x, t;0, 0) $ 的实部和虚部. 绿色菱形和紫色三角形分别展示了$ \psi(x, 0) $ 的实部与虚部Fig. 3. Measured wave function of single photon and
$ K^{\prime\prime}(x, t=20{\rm{\; mm/{\rm{c}}}};0, 0) $ . The green diamond and purple triangle represent the real and imaginary parts of the wave function, respectively. The red dot and the blue square show the real and imaginary parts of the$ K^{\prime\prime}(x, t= $ $ 20{\rm{\; mm/{\rm{c}}}};0, 0) $ at$ t=20 $ mm/c
图 4
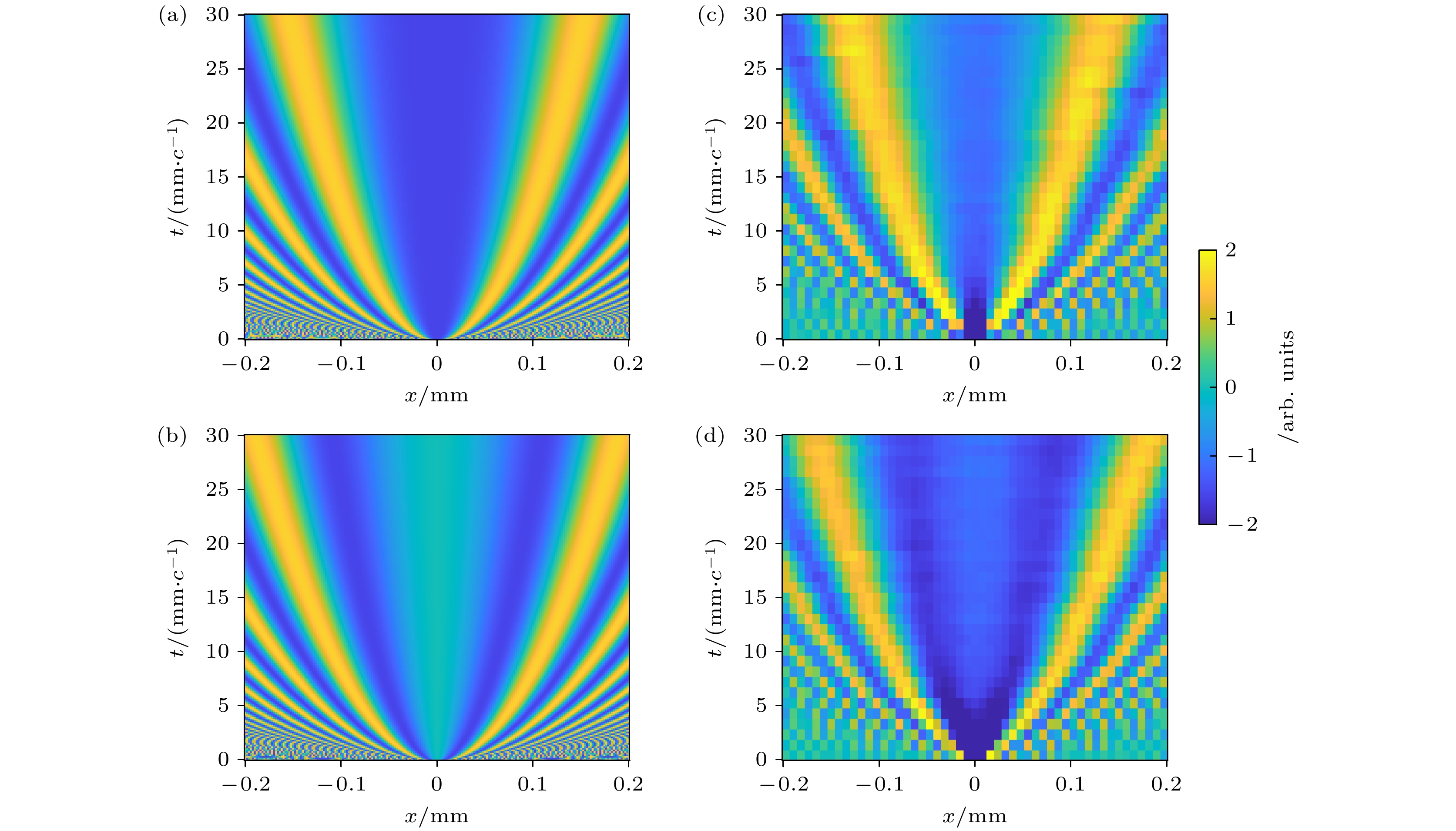
$ K_{\rm{f}}(x, t;x_a, t_a) $ 以x和t为变量的理论与实验结果. 纵轴是演化时间t, 横轴是横向位置x, 颜色代表实部或者虚部的幅度大小. 对演化时间t 每间隔1 mm/c从$ 0 $ 测量到30 mm/c, 横向位置每间隔8 μm从$ -0.2 $ mm测量到0.2 mmFig. 4. Theoretical and experimental results of
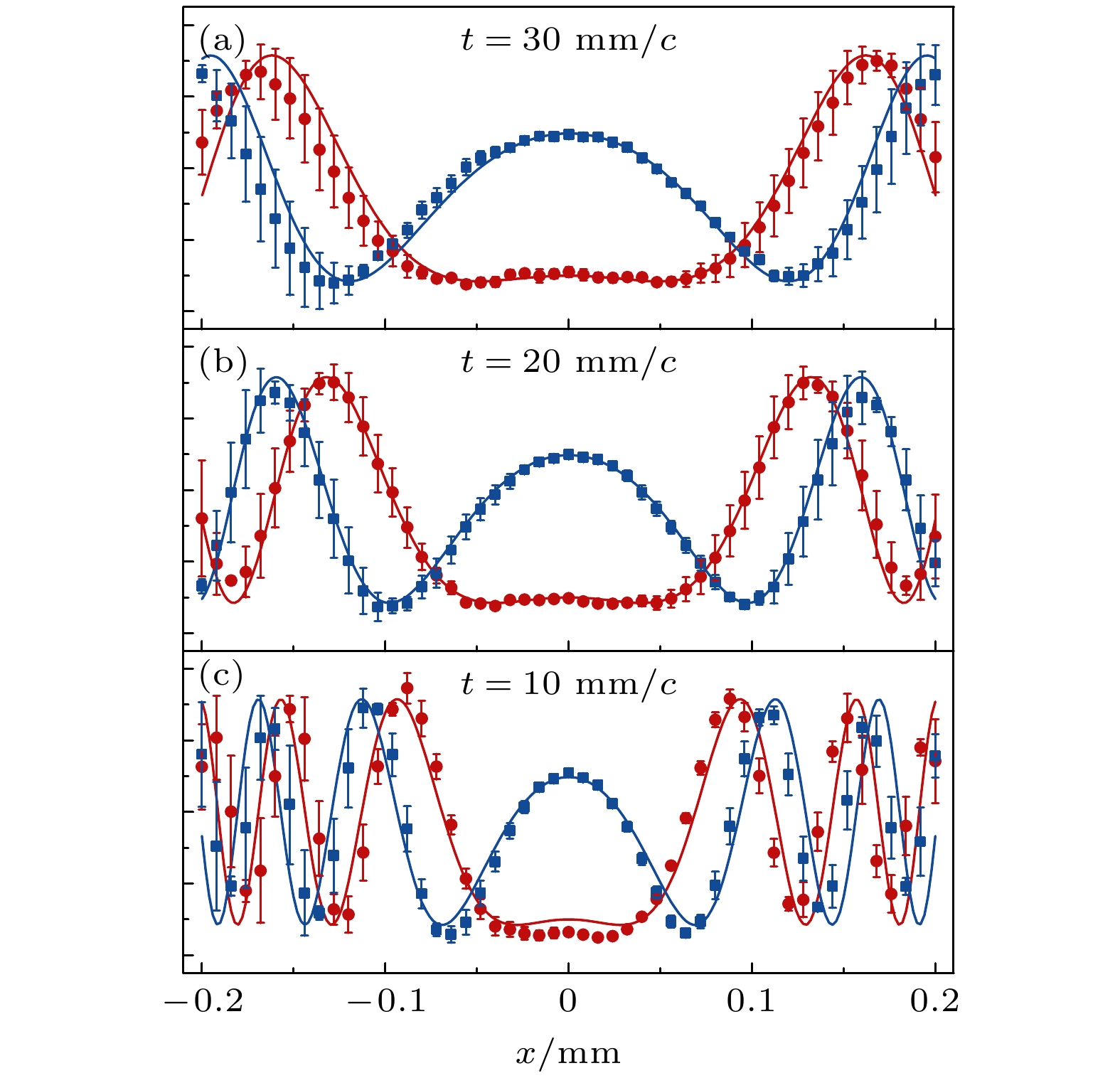
$ K_{\rm{f}}(x_b, t_b;x_a, t_a) $ over time. The vertical axis is the evolution time t, the horizontal axis is the transverse position x. The colormaps represent the magnitude of the real or imaginary part of$ K_{\rm{f}}(x, t;x_a, t_a) $ . Evolution time is measured from$ 0 $ to 30 mm/c at 1 mm/c interval. Transverse positions are measured from$ -0.2 $ mm to 0.2 mm at 8 μm intervals.
图 5 在自由空间中测到的传播子 红线和蓝线是理论计算的传播子实部和虚部的结果, 红色圆圈和蓝色方块是实验测到的数据
Fig. 5. Measured propagators of photons in free space. The red and blue lines are the results of theoretical calculations of the real and imaginary parts of the propagators, and the red circles and blue squares are experimentally measured data.
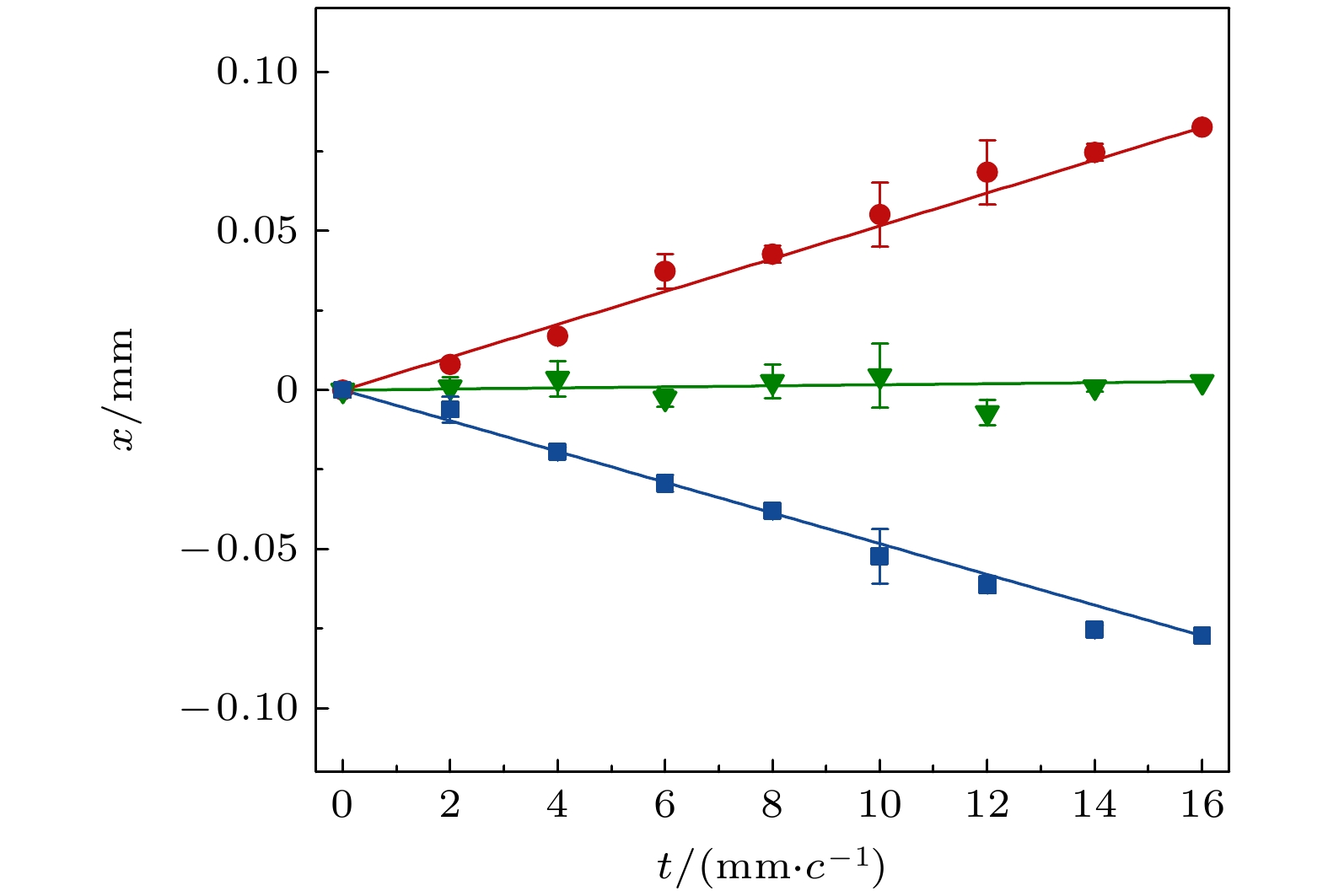
图 6 由最小作用量原理得到的光子自由演化时的经典路径. 实线展示的是理论计算所得的自由演化的经典路径, 离散点为通过传播子的实验数据求得的自由演化的经典路径位置
Fig. 6. The classical path of photons in free evolution derived from the principle of least action. The solid line shows the classical path in free evolution obtained from the theoretical calculation, and the discrete point is the classical path position in free evolution obtained from the experimental data of the propagator.
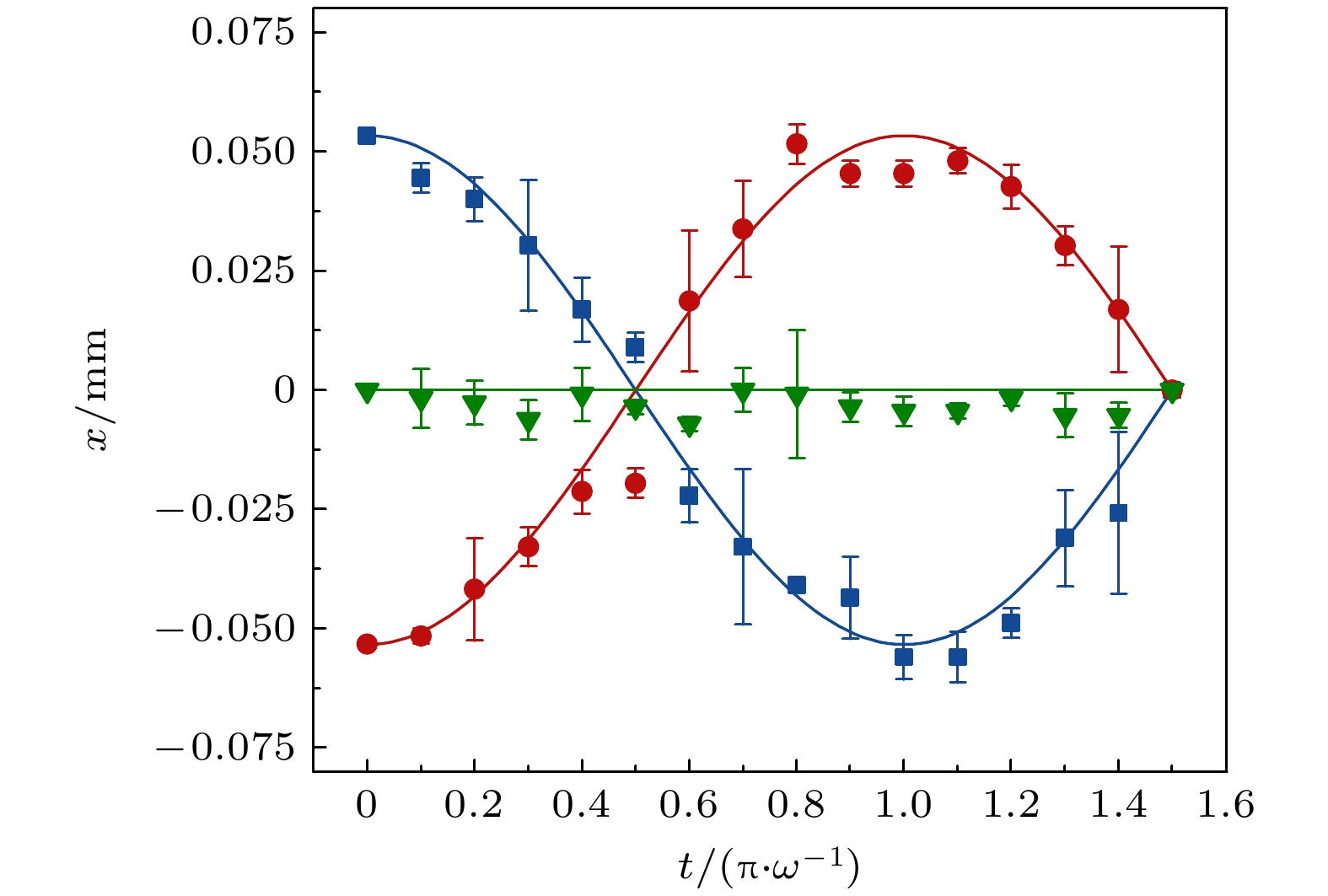
图 7 在谐振子势场中的经典路径. 实线展示的是理论计算所得的在谐振势中的经典路径, 离散点为通过传播子的实验数据求得的在谐振势中的经典路径位置
Fig. 7. Classical trajectories in the harmonic potential. The solid line shows the classical path in the harmonic potential obtained by theoretical calculation, and the discrete point is the classical path position in the harmonic potential obtained by the experimental data of the propagator
-
[1] Feynman R P 1948 Rev. Mod. Phys. 20 367
Google Scholar
[2] Feynman R P 2005 Feynman’s Thesis—A New Approach to Quantum Theory (Singapore: World Scientific Publishing Co Pte Ltd) pp1–69
[3] Feynman R P, Hibbs A R, Styer D F 2010 Quantum Mechanics and Path Integrals (Chelmsford: Courier Corporation) pp1–384
[4] Wen Y L, Wang Y F, Tian L M, Zhang S C, Li J F, Du J S, Yan H, Zhu S L 2023 Nat. Photonics 17 717
Google Scholar
[5] Von Neumann J 2018 Mathematical Foundations of Quantum Mechanics (New Edition) (Princeton: Princeton university press) pp271–288
[6] Aharonov Y, Albert D Z, Vaidman L 1988 Phys. Rev. Lett. 60 1351
Google Scholar
[7] Lundeen J S, Sutherland B, Patel A, Stewart C, Bamber C 2011 Nature 474 188
Google Scholar
[8] Hofheinz M, Wang H, Ansmann M, Bialczak R C, Lucero E, Neeley M, O’Connell A D, Sank D, Wenner J, MartinisJ M, ClelandA N 2009 Nature 459 546
Google Scholar
[9] Cramer M, Plenio M B, Flammia S T, Somma R, Gross D, Bartlett S D, Landon-Cardinal O, Poulin D, Liu Y K 2010 Nat. Commun. 1 149
Google Scholar
[10] Ritchie N W M, Story J G, Hulet R G 1991 Phys. Rev. Lett. 66 1107
Google Scholar
[11] Hosten O, Kwiat P 2008 Science 319 787
Google Scholar
[12] Starling D J, Dixon P B, Jordan A N, Howell J C 2009 Phys. Rev. A 80 041803
Google Scholar
[13] Zhou L, Turek Y, Sun C P, Nori F 2013 Phys. Rev. A 88 053815
Google Scholar
[14] Zhou X X, Xiao Z C, Luo H L, Wen S C 2012 Phys. Rev. A 85 043809
Google Scholar
[15] Rodenburg B, Mirhosseini M, Magaña-Loaiza O S, Boyd R W 2014 JOSA B 3 1
Google Scholar
[16] Magaña-Loaiza O S, Mirhosseini M, Rodenburg B, Boyd R W 2014 Phys. Rev. Lett. 112 200401
Google Scholar
[17] Starling D J, Dixon P B, Williams N S, Jordan A N, Howell J C 2010 Phys. Rev. A 82 011802
Google Scholar
[18] Xu X Y, Kedem Y, Sun K, Vaidman L, Li C F, Guo G C 2013 Phys. Rev. Lett. 111 033604
Google Scholar
[19] Starling D J, Dixon P B, Jordan A N, Howell J C 2010 Phys. Rev. A 82 063822
Google Scholar
[20] Brunner N, Simon C 2010 Phys. Rev. Lett. 105 010405
Google Scholar
[21] Strübi G, Bruder C 2013 Phys. Rev. Lett. 110 083605
Google Scholar
[22] Hallaji M, Feizpour A, Dmochowski G, Sinclair J, Steinberg A M 2017 Nat. Phys. 13 540
Google Scholar
[23] Du S J, Peng Y G, Feng H R, Han F, Yang L W, Zheng Y J 2020 Chin. Phys. B 29 074202
Google Scholar
[24] Zhang C Y, Fang M F 2021 Chin. Phys. B 30 010303
Google Scholar
[25] Dressel J, Malik M, Miatto F M, Jordan A N, Boyd R W 2014 Rev. Mod. Phys. 86 307
Google Scholar
[26] Pfeifer M, Fischer P 2011 Opt. Express 19 16508
Google Scholar
[27] Qiu J D, Li Z X, Xie L G, Luo L, He Y, Ren C L, Zhang Z Y, Du J L 2021 Chin. Phys. B 30 064216
Google Scholar
[28] Fang S Z, Dai Y, Jiang Q W, Tan H T, Li G X, Wu Q L 2021 Chin. Phys. B 30 060601
Google Scholar
[29] Lundeen J S, Resch K J 2005 Phys. Lett. A 334 337
Google Scholar
[30] Salvail J Z, Agnew M, Johnson A S, Bolduc E, Leach J, Boyd R W 2013 Nat. Photonics 7 316
Google Scholar
[31] Malik M, Mirhosseini M, Lavery M P J, Leach J, Padgett M J, Boyd R W 2014 Nat. Commun. 5 3115
Google Scholar
[32] Thekkadath G S, Giner L, Chalich Y, Horton M J, Banker J, Lundeen J S 2016 Phys. Rev. Lett. 117 120401
Google Scholar
[33] Xiao Y, Kedem Y, Xu J S, Li C F, Guo G C 2017 Opt. Express 25 14463
Google Scholar
[34] Xiao Y, Wiseman H M, Xu J S, Kedem Y, Li C F, Guo G C 2019 Sci. Adv. 5 eaav9547
Google Scholar
[35] Cohen E, Pollak E 2018 Phys. Rev. A 98 042112
Google Scholar
[36] Bolduc E, Gariepy G, Leach J 2016 Nat. Commun. 7 10439
Google Scholar
[37] Pan W W, Xu X Y, Kedem Y, Wang Q Q, Chen Z, Jan M, Sun K, Xu J S, Han Y J, Li C F, Guo G C 2019 Phys. Rev. Lett. 123 150402
Google Scholar
[38] Chen M C, Li Y, Liu R Z, Wu D, Su Z E, Wang X L, Li L, Liu N L, Lu C Y, Pan J W 2021 Phys. Rev. Lett. 127 030402
Google Scholar
[39] Kobayashi H, Tamate S, Nakanishi T, Sugiyama K, Kitano M 2010 Phys. Rev. A 81 012104
Google Scholar
[40] Shi Z M, Mirhosseini M, Margiewicz J, Malik M, Rivera F, Zhu Z Y, Boyd R W 2015 Optica 2 388
Google Scholar
[41] Maccone L, Rusconi C C 2014 Phys. Rev. A 89 022122
Google Scholar
[42] Mirhosseini M, Magaña-Loaiza O S, Hashemi Rafsanjani S M, Boyd R W 2014 Phys. Rev. Lett. 113 090402
Google Scholar
[43] Xu L, Xu H C, Jiang T, Xu F X, Zheng K M, Wang B, Zhang A N, Zhang L J 2021 Phys. Rev. Lett. 127 180401
Google Scholar
[44] Piacentini F, Avella A, Levi M P, Gramegna M, Brida G, Degiovanni I P, Cohen E, Lussana R, Villa F, Tosi A, Zappa F, Genovese M 2016 Phys. Rev. Lett. 117 170402
Google Scholar
[45] Shojaee E, Jackson C S, Riofrío C A, Kalev A, Deutsch I H 2018 Phys. Rev. Lett. 112 130404
Google Scholar
[46] Bamber C, Lundeen J S 2014 Phys. Rev. Lett. 112 070405
Google Scholar
[47] Wu S J 2013 Sci. Rep. 3 1193
Google Scholar
[48] Kocsis S, Braverman B, Ravets S, Stevens M J, Mirin R P, Shalm L K, Steinberg A M 2011 Science 332 1170
Google Scholar
[49] Wen Y L, Zhang S C, Yan H, Zhu S L 2022 Chin. Phys. B 31 034206
Google Scholar
[50] 温永立, 张善超, 颜辉, 朱诗亮 2021 70 110301
Google Scholar
Wen Y L, Zhang S C, Yan H, Zhu S L 2021 Acta Phys. Sin. 70 110301
Google Scholar
[51] Romito A, Gefen Y 2014 Phys. Rev. B 90 085417
Google Scholar
[52] Vallone G, Dequal D 2016 Phys. Rev. Lett. 116 040502
Google Scholar
[53] Zhang S C, Zhou Y R, Mei Y F, Liao K Y, Wen Y L, Li J F, Zhang X D, Du S W, Yan H, Zhu S L 2019 Phys. Rev. Lett. 123 190402
Google Scholar
[54] Zhang C R, Hu M J, Hou Z B, Tang J F, Zhu J, Xiang G Y, Li C F, Guo G C, Zhang Y S 2020 Phys. Rev. A 101 012119
Google Scholar
[55] Zhang C R, Hu M J, Xiang G Y, Zhang Y S, Li C F, Guo G C 2020 Chin. Phys. Lett. 37 080301
Google Scholar
[56] Zhou Y Y, Zhao J, Hay D, McGonagle K, Boyd R W, Shi Z M 2021 Phys. Rev. Lett. 127 040402
Google Scholar
[57] Yang M, Xiao Y, Liao Y W, Liu Z H, Xu X Y, Xu J S, Li C F, Guo G C 2020 Laser Photonics Rev. 14 1900251
Google Scholar
[58] Calderaro L, Foletto G, Dequal D, Villoresi P, Vallone G 2018 Phys. Rev. Lett. 121 230501
Google Scholar
[59] Knarr S H, Lum D J, Schneeloch J, Howell J C 2018 Phys. Rev. A 98 023854
Google Scholar
[60] Pan Y M, Zhang J, Cohen E, Wu C W, Chen P X, Davidson N 2020 Nat. Phys. 16 1206
Google Scholar
[61] Rojo A, Bloch A 2018 The Principle of Least Action: History and Physics (Cambridg: Cambridge University Press) pp1–266
[62] 朱诗亮, 温永立, 颜辉 2023 物理 52 502
Google Scholar
Zhu S L, Wen Y L, Yan H 2023 Physics 52 502
Google Scholar
[63] Salières P, Carré B, Le Déroff L, Grasbon F, Paulus G G, Walther H, Kopold R, Becker W, Milosevic D B, Sanpera A, Lewenstein M 2001 Science 292 902
Google Scholar
[64] Gibbons G W, Hawking S W, Perry M J 1978 Nucl. Phys. B 138 141
Google Scholar
[65] Fujikawa K 1979 Phys. Rev. Lett. 42 1195
Google Scholar
[66] Ord G N, Gualtieri J A 2002 Phys. Rev. Lett. 89 250403
Google Scholar
[67] Caldeira A O, Leggett A J 1983 Physica A 121 587
Google Scholar
[68] Mühlbacher L, Rabani E 2008 Phys. Rev. Lett. 100 176403
Google Scholar
[69] Pollock E L, Ceperley D M 1984 Phys. Rev. B 30 2555
Google Scholar
[70] Reisenberger M P, Rovelli C 1997 Phys. Rev. D 56 3490
Google Scholar
[71] Hartle J B, Hawking S W 1983 Phys. Rev. D 28 2960
Google Scholar
[72] Ashtekar A, Campiglia M, Henderson A 2010 Phys. Rev. D 82 124043
Google Scholar
[73] Fujikawa K 1982 Phys. Rev. D 25 2584
Google Scholar
[74] Hartle J B, Hawking S W 1976 Phys. Rev. D 13 2188
Google Scholar
下载:
计量
- 文章访问数: 2281
- PDF下载量: 85
- 被引次数: 0
