-
量子计算相比于经典计算在处理某些复杂性问题时具有与生俱来的独特优势, 从而受到广泛关注. 要想实现大规模的量子计算, 最关键的在于不断提高量子比特的保真度. 由于量子比特的脆弱性, 环境热噪声对其保真度具有极大影响. 本文基于偶极场驱动量子比特的方式, 采取随机动力学结构分解方法, 并应用久保-爱因斯坦涨落耗散定理研究热噪声环境下的量子比特控制问题. 偶极场具有3个方向的分量, 而不仅仅只限于一个平面, 这种控制方式可以更加灵活地控制量子态. 在不考虑噪声的情况下, 量子态能够100%的到达目标态. 而在噪声环境中, 热噪声会使得实际终态和目标终态存在由热涨落造成的偏差, 成为影响量子保真度的主要因素. 为此本文利用蒙特卡罗优化算法对驱动场进行优化, 以此来进一步提高量子比特保真度. 该方法的可行性在数值计算中得到了验证, 可以为实验提供新的解决方案, 用以进一步指导和评估实验.Quantum computing is a new way to process quantum information by using superposition and entanglement of the quantum system. Quantum state’s vast Hilbert space allows it to perform operations that classical computers cannot. The quantum computing has unique advantages in dealing with some complex problems, so it has attracted wide attention. Computing a single qubit is the first of seven fundamental stages needed to achieve a large-scale quantum computer that is universal, scalable and fault-tolerant. In other words, the primary task of quantum computing is the careful preparation and precise regulation of qubits. At present, the physical systems that can be used as qubits include superconducting qubits, semiconductor qubits, ion trap systems and nitrogen-vacancy (NV) color centers. These physical systems have made great progress of decoherence time and scalability. Owing to the vulnerability of qubits, ambient thermal noise can cause quantum decoherence, which greatly affects the fidelity of qubits. Improving the fidelity of qubits is therefore a key step towards large-scale quantum computing. Based on the dipole field driven qubit, the stochastic dynamic structure decomposition method is adopted and the Kubo-Einstein fluctuation-dissipation theorem is used to study the qubit control in a thermal noise environment. The dipole field has components in three directions, not just in one plane, which allows more flexible control of quantum states. Without considering the noise, the quantum state can reach the target state 100%. In the noisy environment, thermal noise will cause the deviation between the actual final state and the target final state caused by thermal fluctuation, which becomes the main factor affecting the quantum fidelity. The influence of thermal noise is related to temperature and the evolution trajectory of quantum state. Therefore, this paper proposes an optimal scheme to improve the qubit fidelity in the thermal noise environment. The feasibility of this method is verified by numerical calculation, which can provide a new solution for further guiding and evaluating the experiment. The scheme is suitable for qubit systems of various physical control fields, such as semiconductor qubits and nitrogen vacancy center qubits. This work may have more applications in the development of quantum manipulation technology and can also be extended to multi-qubit systems, the details of which will appear in the future work.
-
Keywords:
- qubits /
- dipole fields /
- thermal noise /
- fidelity
[1] Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45
Google Scholar
[2] Grover L K 1997 Phys. Rev. Lett. 79 325
Google Scholar
[3] Shor P W 1994 SIAM J. Comput. 26 1484
[4] Devoret M H, Schoelkopf R J 2013 Science 339 1169
Google Scholar
[5] Chiorescu I, Nakamura Y, Harmans C J, Mooij J E 2003 Science 299 1869
Google Scholar
[6] Blais A, Huang R S, Wallraff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 062320
Google Scholar
[7] Koch J, Yu T M, Gambetta J, et al. 2007 Phys. Rev. A 76 042319
Google Scholar
[8] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[9] Kastner J H, Richmond M, Grosso N, et al. 2004 Nature 430 429
Google Scholar
[10] Veldhorst M, Yang C H, Hwang J C, et al. 2015 Nature 526 410
Google Scholar
[11] Haffner H, Roos C, Blatt R 2008 Phys. Rep. 469 155
Google Scholar
[12] Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504
Google Scholar
[13] Balasubramanian G, Neumann P, Twitchen D, et al. 2009 Nat. Mater. 8 383
Google Scholar
[14] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[15] Ahn J, Weinacht T C, Bucksbaum P H 2000 Science 287 463
Google Scholar
[16] He Y, Gorman S K, Keith D, Kranz L, Keizer J G, Simmons M Y 2019 Nature 571 371
Google Scholar
[17] Sarandy M S, Lidar D A 2005 Phys. Rev. Lett. 95 250503
Google Scholar
[18] Barends R, Shabani A, Lamata L, et al. 2016 Nature 534 222
Google Scholar
[19] Emmanouilidou A, Zhao X G, Ao P, Niu Q 2000 Phys. Rev. Lett. 85 1626
Google Scholar
[20] Guéry-Odelin D, Ruschhaupt A, Kiely A, Torrontegui E, Martínez-Garaot S, Muga J G 2019 Rev. Mod. Phys. 91 045001
Google Scholar
[21] Berry M V 2009 J. Phys. A Math. Theor. 42 365303
Google Scholar
[22] Zurek W H 2003 Rev. Mod. Phys. 75 715
Google Scholar
[23] Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser S J 2005 J. Magn. Reson. 172 296
Google Scholar
[24] Konnov A I, Krotov V F 1999 Avtom. i Telemekhanika 10 77
[25] Wu R B, Chu B, Owens D H, Rabitz H 2018 Phys. Rev. A 97 042122
Google Scholar
[26] Eitan R, Mundt M, Tannor D J 2011 Phys. Rev. A 83 053426
Google Scholar
[27] Hwang B, Goan H S 2012 Phys. Rev. A 85 032321
Google Scholar
[28] Rebentrost P, Serban I, Schulte-Herbrüggen T, Wilhelm F K 2009 Phys. Rev. Lett. 102 090401
Google Scholar
[29] Manzano D 2020 AIP. Adv. 10 025106
Google Scholar
[30] Benedetti C, Paris M G A, Maniscalco S 2014 Phys. Rev. A 89 012114
Google Scholar
[31] Bhattacharya S, Chaudhury P, Chattopadhyay S, Chaudhri J R 2008 Phys. Rev. E 78 021123
Google Scholar
[32] Alscher A, Grabert H 1999 J. Phys. A Math. Gen. 32 4907
Google Scholar
[33] Ao P 2004 J. Phys. A Math. Gen. 37 L25
Google Scholar
[34] Chen Y C, Lebowitz J L, Liverani C 1989 Phys. Rev. B 40 4664
Google Scholar
[35] Kubo R 1966 Rep. Prog. Phys. 29 255
Google Scholar
[36] Kwon C, Ao P, Thouless D J 2005 Proc. Natl. Acad. Sci. U. S. A. 102 13029
Google Scholar
[37] Chen Y C 1987 J. Stat. Phys. 47 17
Google Scholar
[38] 刘学铭 2022 硕士学位论文 (上海: 上海大学)
Liu X M 2022 M. S. Dissertation (Shanghai: Shanghai University) (in Chinese)
[39] Wesenberg J H, Ardavan A, Briggs G A, Morton J J, Schoelkopf R J, Schuster D I, Molmer K 2009 Phys. Rev. Lett. 103 070502
Google Scholar
[40] Takeda K, Noiri A, Nakajima T, Yoneda J, Kobayashi T, Tarucha S 2021 Nat. Nanotechnol. 16 965
Google Scholar
[41] Pla J J, Tan K Y, Dehollain J P, Lim W H, Morton J J L, Jamieson D N, Dzurak A S, Morello A 2012 Nature 489 541
Google Scholar
[42] Tetienne J P, Rondin L, Spinicelli P, Chipaux M, Debuisschert T, Roch J F, Jacques V 2012 New. J. Phys. 14 103033
Google Scholar
[43] Caldeira A O, Leggett A J 1983 Ann. Phys. 149 374
Google Scholar
[44] Feynman R P, Vernon Jr F L 1963 Ann. Phys. 24 118
Google Scholar
-
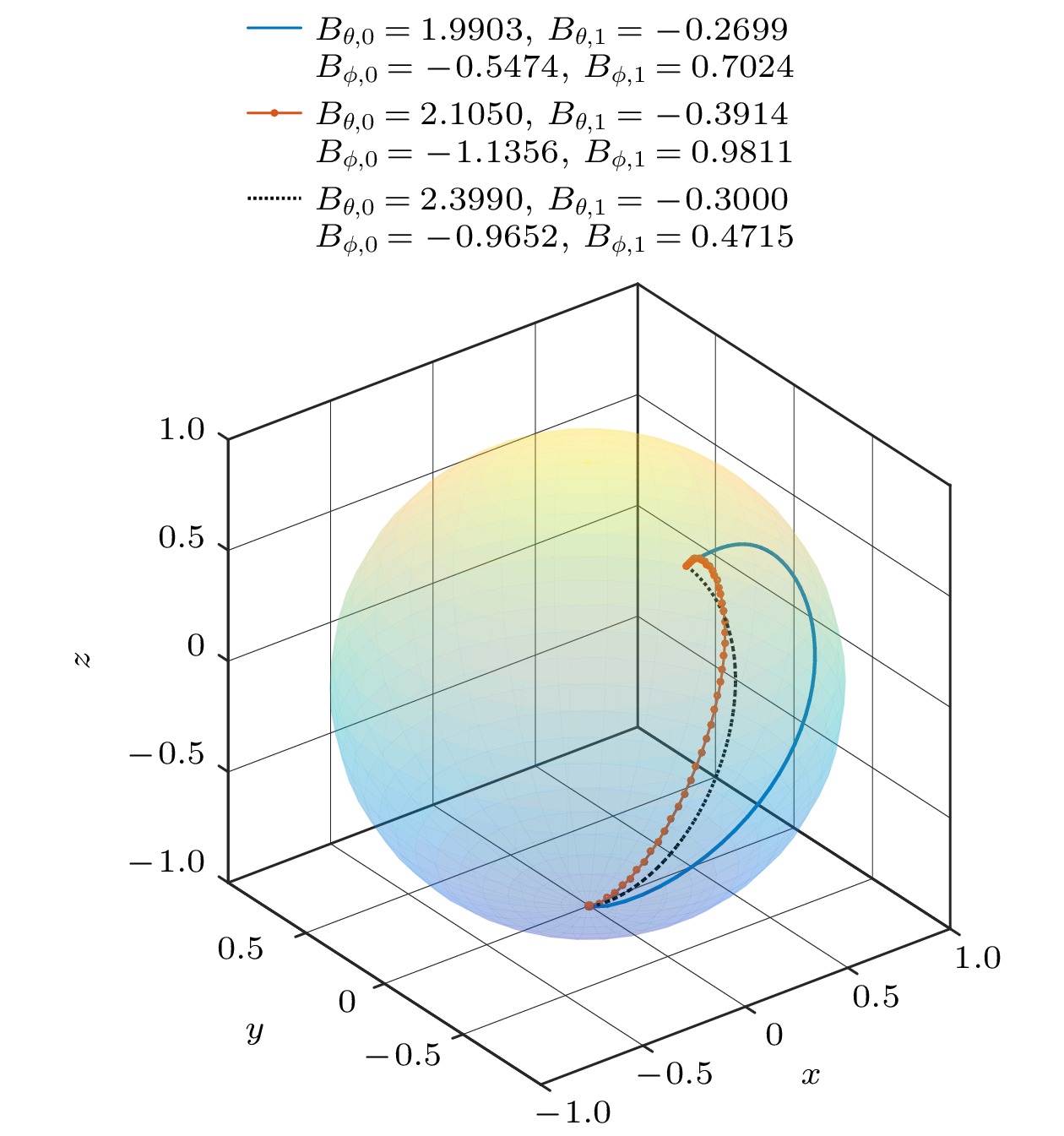
图 1 在无噪声环境下, 初态为
$\left( {{\text{π/2, π}}/6} \right)$ , 末态为$\left( {{\text{π, π}}/3} \right)$ 的量子态在布洛赫球上不同的演化轨迹, 其保真度都为1Fig. 1. In the noiseless environment, the quantum states with initial state
$\left( {{\text{π/2, π}}/6} \right)$ and final state$\left( {{\text{π, π}}/3} \right)$ have different evolutionary trajectora on the Bloch sphere. They all have a fidelity of 1.
图 2 噪声环境下, 初态为
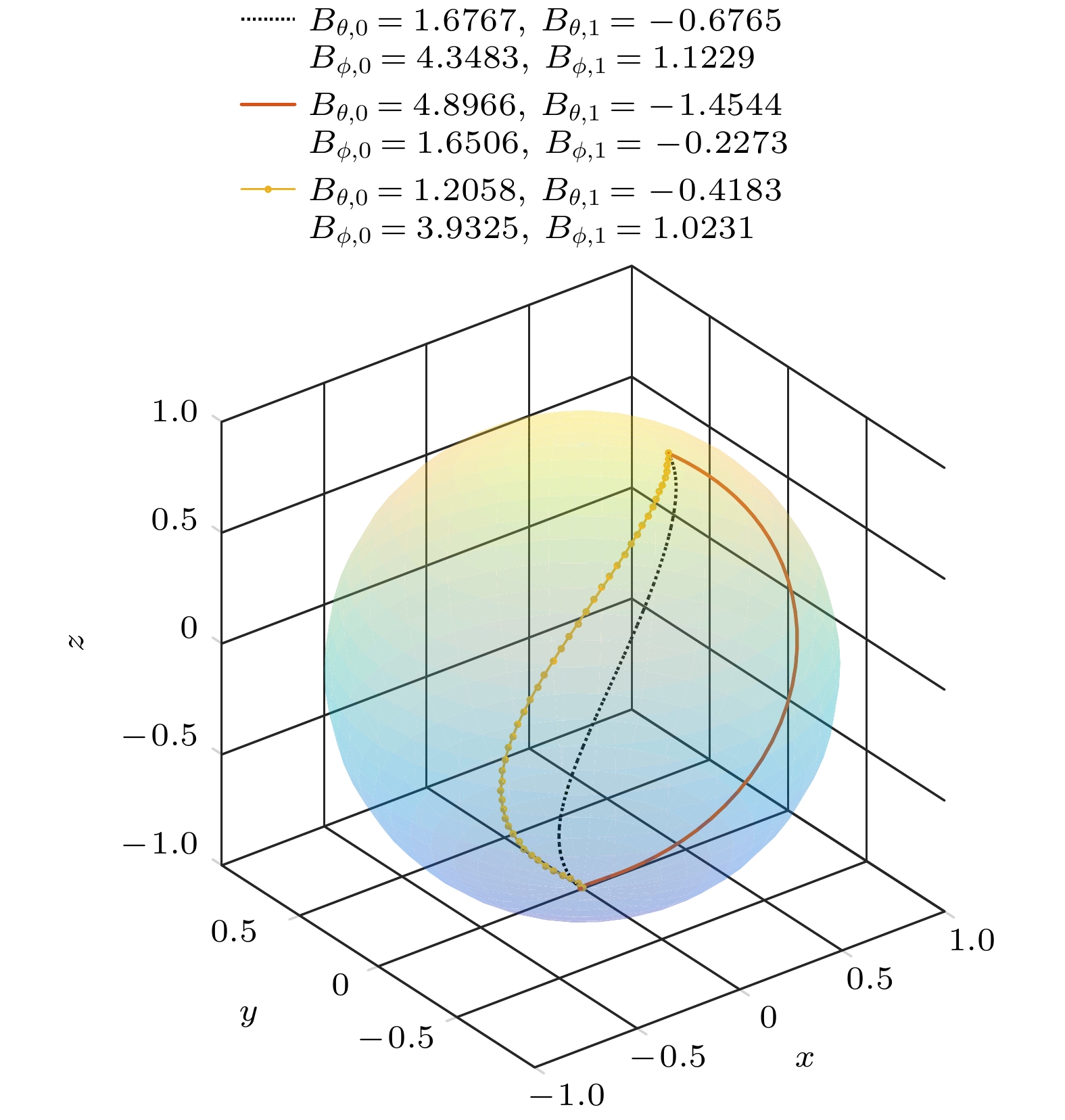
$\left( {{\text{π/2, π}}/6} \right)$ , 末态为$\left( {{\text{π, π}}/3} \right)$ 的量子态在布洛赫球上不同的演化轨迹, 其保真度分别为实线: 0.9996; 点实线: 0.9995; 点线: 0.9996Fig. 2. In the noisy environment, the quantum states of the initial state
$\left( {{\text{π/2, π}}/6} \right)$ and the final state$\left( {{\text{π, π}}/3} \right)$ have different evolution tracks on the Bloch sphere. Their fidelity is respectively solid line: 0.9996; dot solid line: 0.9995; dot line: 0.9996.
图 3 噪声环境下, 初态为
$\left( {{\text{π/2, π}}/6} \right)$ , 末态为$\left( {{\text{π, π}}/3} \right)$ 的量子态在布洛赫球上不同的演化轨迹, 其保真度分别为点线: 0.9988; 实线: 0.9996; 点实线: 0.9986Fig. 3. In the noisy environment, the quantum states of the initial state
$\left( {{\text{π/2, π}}/6} \right)$ and the final state$\left( {{\text{π, π}}/3} \right)$ have different evolution tracks on the Bloch sphere. Their fidelity is respectively dot line: 0.9988; solid line: 0.9996; dot solid line: 0.9986. -
[1] Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45
Google Scholar
[2] Grover L K 1997 Phys. Rev. Lett. 79 325
Google Scholar
[3] Shor P W 1994 SIAM J. Comput. 26 1484
[4] Devoret M H, Schoelkopf R J 2013 Science 339 1169
Google Scholar
[5] Chiorescu I, Nakamura Y, Harmans C J, Mooij J E 2003 Science 299 1869
Google Scholar
[6] Blais A, Huang R S, Wallraff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 062320
Google Scholar
[7] Koch J, Yu T M, Gambetta J, et al. 2007 Phys. Rev. A 76 042319
Google Scholar
[8] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[9] Kastner J H, Richmond M, Grosso N, et al. 2004 Nature 430 429
Google Scholar
[10] Veldhorst M, Yang C H, Hwang J C, et al. 2015 Nature 526 410
Google Scholar
[11] Haffner H, Roos C, Blatt R 2008 Phys. Rep. 469 155
Google Scholar
[12] Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504
Google Scholar
[13] Balasubramanian G, Neumann P, Twitchen D, et al. 2009 Nat. Mater. 8 383
Google Scholar
[14] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1
Google Scholar
[15] Ahn J, Weinacht T C, Bucksbaum P H 2000 Science 287 463
Google Scholar
[16] He Y, Gorman S K, Keith D, Kranz L, Keizer J G, Simmons M Y 2019 Nature 571 371
Google Scholar
[17] Sarandy M S, Lidar D A 2005 Phys. Rev. Lett. 95 250503
Google Scholar
[18] Barends R, Shabani A, Lamata L, et al. 2016 Nature 534 222
Google Scholar
[19] Emmanouilidou A, Zhao X G, Ao P, Niu Q 2000 Phys. Rev. Lett. 85 1626
Google Scholar
[20] Guéry-Odelin D, Ruschhaupt A, Kiely A, Torrontegui E, Martínez-Garaot S, Muga J G 2019 Rev. Mod. Phys. 91 045001
Google Scholar
[21] Berry M V 2009 J. Phys. A Math. Theor. 42 365303
Google Scholar
[22] Zurek W H 2003 Rev. Mod. Phys. 75 715
Google Scholar
[23] Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser S J 2005 J. Magn. Reson. 172 296
Google Scholar
[24] Konnov A I, Krotov V F 1999 Avtom. i Telemekhanika 10 77
[25] Wu R B, Chu B, Owens D H, Rabitz H 2018 Phys. Rev. A 97 042122
Google Scholar
[26] Eitan R, Mundt M, Tannor D J 2011 Phys. Rev. A 83 053426
Google Scholar
[27] Hwang B, Goan H S 2012 Phys. Rev. A 85 032321
Google Scholar
[28] Rebentrost P, Serban I, Schulte-Herbrüggen T, Wilhelm F K 2009 Phys. Rev. Lett. 102 090401
Google Scholar
[29] Manzano D 2020 AIP. Adv. 10 025106
Google Scholar
[30] Benedetti C, Paris M G A, Maniscalco S 2014 Phys. Rev. A 89 012114
Google Scholar
[31] Bhattacharya S, Chaudhury P, Chattopadhyay S, Chaudhri J R 2008 Phys. Rev. E 78 021123
Google Scholar
[32] Alscher A, Grabert H 1999 J. Phys. A Math. Gen. 32 4907
Google Scholar
[33] Ao P 2004 J. Phys. A Math. Gen. 37 L25
Google Scholar
[34] Chen Y C, Lebowitz J L, Liverani C 1989 Phys. Rev. B 40 4664
Google Scholar
[35] Kubo R 1966 Rep. Prog. Phys. 29 255
Google Scholar
[36] Kwon C, Ao P, Thouless D J 2005 Proc. Natl. Acad. Sci. U. S. A. 102 13029
Google Scholar
[37] Chen Y C 1987 J. Stat. Phys. 47 17
Google Scholar
[38] 刘学铭 2022 硕士学位论文 (上海: 上海大学)
Liu X M 2022 M. S. Dissertation (Shanghai: Shanghai University) (in Chinese)
[39] Wesenberg J H, Ardavan A, Briggs G A, Morton J J, Schoelkopf R J, Schuster D I, Molmer K 2009 Phys. Rev. Lett. 103 070502
Google Scholar
[40] Takeda K, Noiri A, Nakajima T, Yoneda J, Kobayashi T, Tarucha S 2021 Nat. Nanotechnol. 16 965
Google Scholar
[41] Pla J J, Tan K Y, Dehollain J P, Lim W H, Morton J J L, Jamieson D N, Dzurak A S, Morello A 2012 Nature 489 541
Google Scholar
[42] Tetienne J P, Rondin L, Spinicelli P, Chipaux M, Debuisschert T, Roch J F, Jacques V 2012 New. J. Phys. 14 103033
Google Scholar
[43] Caldeira A O, Leggett A J 1983 Ann. Phys. 149 374
Google Scholar
[44] Feynman R P, Vernon Jr F L 1963 Ann. Phys. 24 118
Google Scholar
下载:
计量
- 文章访问数: 2917
- PDF下载量: 75
- 被引次数: 0
