-
动力学解耦技术能有效地抑制由低频环境噪声导致的退相干过程, 因此在量子信息领域获得了广泛的应用. 传统的动力学解耦方案通过对简单的二能级体系, 如量子比特, 施加特定的π脉冲序列来实现解耦效果. 随着量子计算研发的深入, 对于像超导量子比特这种天然的多能级系统, 研究者不再局限于二能级子空间, 而是提出和实现了一系列基于多能级体系的量子调控手段和量子算法. 目前对于如何抑制这些体系中的退相干尚缺乏深入研究. 本文利用较易在实验中实现的紧邻能级间的π脉冲, 构建了多种针对多能级系统的动力学解耦序列. 结果表明这些序列可以很好地消除准静态噪声的影响. 此外, 通过计算滤波函数, 还分析了这些序列及其拓展方案对于高斯噪声的抑制作用, 并结合控制函数对滤波效果给出了物理解释. 研究结果对于多能级体系中的相关噪声研究, 包括噪声功率谱密度和关联性的刻画以及退相干的抑制等, 均具有启发意义.
Dynamical decoupling refers to a family of techniques that are widely used to suppress decoherence in various quantum systems, caused by quasi-static environmental noise. They have broad applications in the field of quantum information processing. Conventional dynamical decoupling targets at noise in two-level system such as qubits and often consists of specifically engineered sequences of $ \pi $ pulses that swap between two different states. On the other hand, researchers do not limit their study within simple two-levels systems any more, but go and seek for even more efficient quantum hardware. A variety of quantum algorithms and schemes of quantum control using multi-level systems, such as qutrits and qudits, for quantum information processing have been proposed and implemented successfully. However, decoherence in such a multi-level system is inherently more sophisticated than that in two-level systems. So far there has been little systematic research on how to tackle decoherence problems in such systems.In this work, we propose several sequences of dynamical decoupling for multi-level systems that only rely on $ \pi $ pulses linking neighboring levels, which is easy to implement experimentally. Our results show that these sequences can efficiently suppress quasi-static noise presented in multi-level systems. In addition, by calculating the corresponding filter functions of these sequences, we are able to further analyze their effect on generic Gaussian noise that may not be quasi-static. We also give a physical explanation of the noise filtering mechanism of these sequences by considering their control functions. Other topics discussed in our work include power spectral density and correlation of noise in multi-level systems. Our work may be regarded as a first step towards a more systematic investigation of dynamical decoupling techniques applicable to multi-level systems.-
Keywords:
- multi-level system /
- noise /
- decoherence /
- dynamic decoupling /
- filter function
[1] Clerk A A, Devoret M H, Girvin S M, Marquardt F, Schoelkopf R J 2010 Rev. Mod. Phys. 82 1155
Google Scholar
[2] Hahn E L 1950 Phys. Rev. 80 580
Google Scholar
[3] Slichter C P 1990 Principles of Nuclear Magnetic Resonance (3rd Ed.) (NewYork: Springer) pp1–7
[4] Viola L, Lloyd S 1998 Phys. Rev. A 58 2733
Google Scholar
[5] Carr H Y, Purcell E M 1954 Phys. Rev. 94 630
Google Scholar
[6] Meiboom S, Gill D 1958 Rev. Sci. Instrum. 29 688
Google Scholar
[7] Grégoire I 2005 Ph. D. Dissertation (Paris: Université Pierre et Marie Curie - Paris VI)
[8] Khodjasteh K, Lidar D A 2005 Phys. Rev. Lett. 95 180501
Google Scholar
[9] Khodjasteh K, Lidar D A 2007 Phys. Rev. A 75 062310
Google Scholar
[10] Uhrig G S 2007 Phys. Rev. Lett. 98 100504
Google Scholar
[11] Uhrig G S 2009 Phys. Rev. Lett. 102 120502
Google Scholar
[12] Uhrig G S 2008 New J. Phys. 10 083024
Google Scholar
[13] Uhrig G S, Pasini S 2010 New J. Phys. 12 045001
Google Scholar
[14] Bylander J, Gustavsson S, Yan F, Yoshihara F, Harrabi K, Fitch G, Oliver W D 2011 Nat. Phys. 7 565
Google Scholar
[15] Gustavsson S, Bylander J, Yan F, Forn-Díaz P, Bolkhovsky V, Braje D, Oliver W D 2012 Phys, Rev. Lett. 108 170503
Google Scholar
[16] Qiu J, Zhou Y, Hu C K, Yuan J, Zhang L, Chu J, Huang W, Liu W, Luo K, Ni Z, Pan X, Yu D 2021 Phys. Rev. A 16 054047
Google Scholar
[17] Google 2023 Nature 614 676
Google Scholar
[18] Gottesman D 1999 Chaos Solitons Fractals 10 1749
Google Scholar
[19] Grassl M, Rötteler M, Beth T 2003 Inter. J. Foundat. Compu. Sci. 14 757
Google Scholar
[20] Bullock S S, OLeary D P, Brennen G K 2005 Phys. Rev. Lett. 94 230502
Google Scholar
[21] Campbell E T, Anwar H, Browne D E 2012 Phys. Rev. X 2 041021
Google Scholar
[22] Campbell E T 2014 Phys. Rev. Lett. 113 230501
Google Scholar
[23] Anwar H, Brown B J, Campbell E T, Browne D E 2014 New J. Phys. 16 063038
Google Scholar
[24] Krishna A, Tillich J P 2019 Phys. Rev. Lett. 123 070507
Google Scholar
[25] Chu J, He X, Zhou Y, Yuan J, Zhang L, Guo Q, Hai Y, Han Z, Hu C K, Huang W, Jia H, Yu D 2023 Nat. Phys. 19 126
Google Scholar
[26] Luo K, Huang W, Tao Z, Zhang L, Zhou Y, Chu J, Liu W, Wang B, Cui J, Liu S, Yan F, Yu D 2023 Phys. Rev. Lett. 130 030603
Google Scholar
[27] Blok M S, Ramasesh V V, Schuster T, O’Brien K, Kreikebaum J M, Dahlen D, Morvan A, Yoshida B, Yao N Y, Siddiqi I 2021 Phys. Rev. X 11 021010
Google Scholar
[28] Suslov M V, Lesovik G B, Blatter G 2011 Phys. Rev. A 83 052317
Google Scholar
[29] Bouchard F, Fickler R, Boyd R W, Karimi E 2017 Sci. Adv. 3 e1601915
Google Scholar
[30] Napolitano R J, Fanchini F F, da Silva A H, Bellomo B 2021 Phys. Rev. Research 3 013235
Google Scholar
[31] Mukhtar M, Saw T B, Soh W T, Gong J 2010 Phys. Rev. A 81 012331
Google Scholar
[32] Koch J, Terri M Y, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys, Rev. A 76 042319
Google Scholar
-
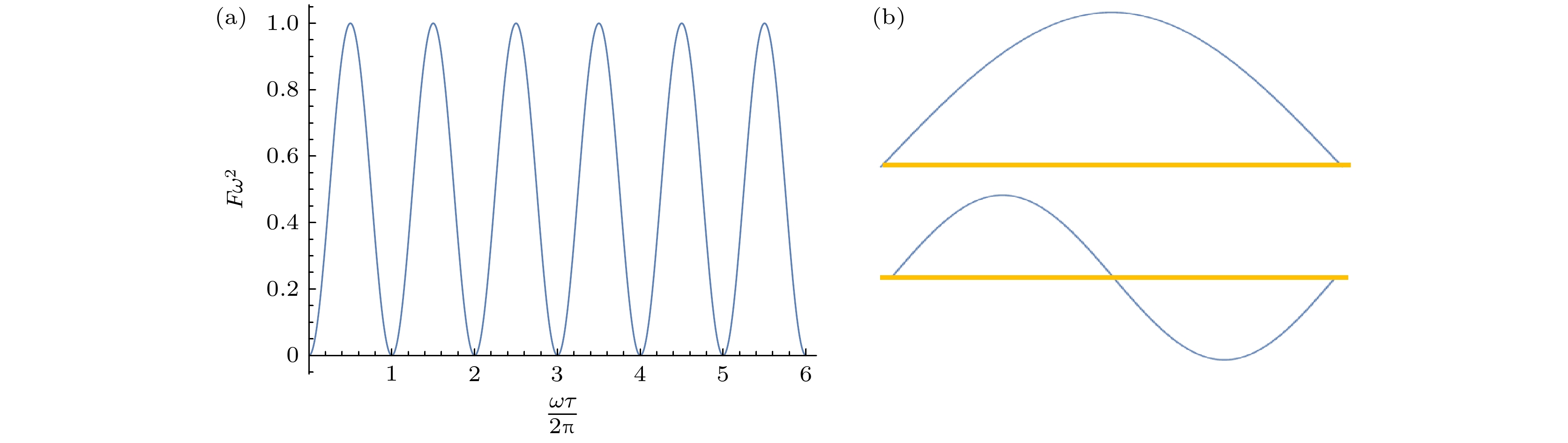
图 1 针对三能级体系的动力学解耦脉冲序列、能级演化及控制函数 (a) 动力学解耦序列, 脉冲施加的时刻分别为
${t}_{1}, {t}_{2}, \cdots, {t}_{6}$ ,$ {t}_{0}, {t}_{6} $ 是整个序列开始和结束的时刻; (b) 不同初态在演化过程中的变化, 每个初态都走遍了不同的能级; (c), (d) 分别是$|0\rangle$ ,$|1\rangle$ 之间和$|0\rangle, \;|2\rangle$ 之间的控制函数Fig. 1. Pulse sequence for dynamical decoupling, state evolution and control function in the case of a three-level system: (a) The pulse sequence;
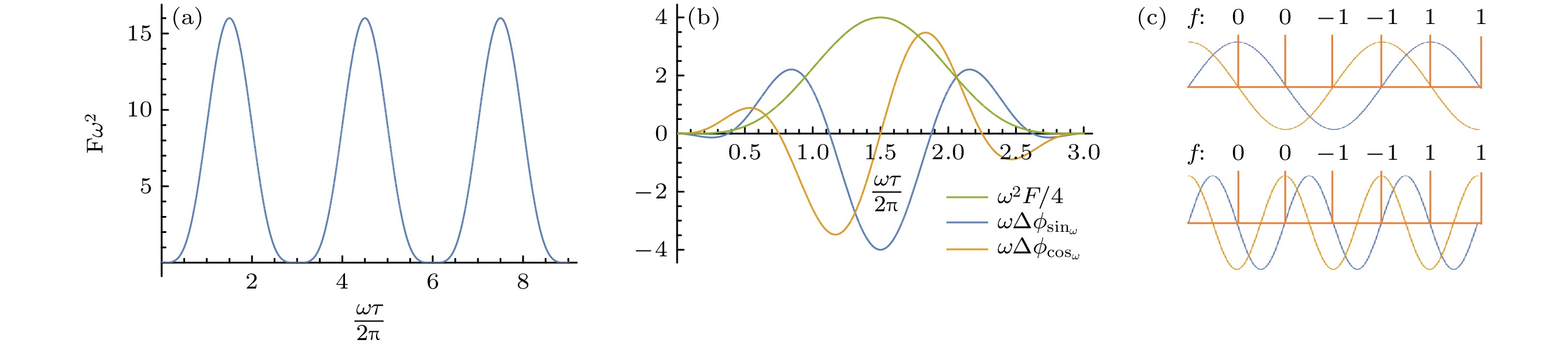
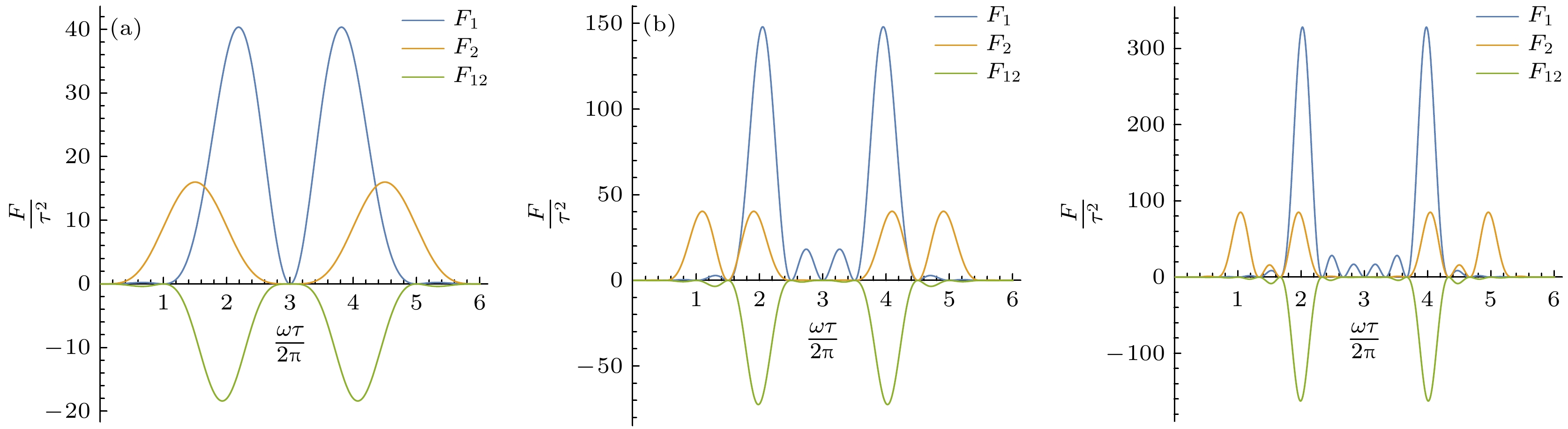
$ \pi $ pulses are applied at time${t}_{1}, {t}_{2}, \cdots, {t}_{6},$ $ {t}_{0}, {t}_{6} $ are the start and end moments of the whole sequence; (b) evolution of different initial states; each state is sequentially flipped into all other states by the$ \pi $ pulses in the sequence; (c), (d) plot the control functions linking states$|0\rangle$ ,$|1\rangle$ and$|0\rangle$ ,$|2\rangle$ , respectively.
图 2 滤波函数 (a)所有
$ \pi $ 脉冲等间隔分布; (b)一次重复中的两个$ \pi $ 脉冲间隔为零Fig. 2. Filter functions: (a) For equal intervals between consecutive pulses; (b) for zero interval between the two pulses during one repetition.
图 3 二能级体系Ramsey过程的滤波函数的周期性 (a) 去掉衰减项后的滤波函数; (b) 操作时间内的噪声周期数
Fig. 3. Periodicity of the Ramsey filter function: (a) The filter function without the attenuation term; (b) noise period during operation time.
图 4 三能级体系滤波函数的周期性 (a)
$F=\dfrac{1}{{\omega }^{2}}16{\rm{s}}{\rm{i}}{\rm{n}}{\left(\dfrac{\omega \tau }{6}\right)}^{4}$ 中的周期部分; (b)$F{\omega }^{2}, \omega \varDelta {\phi }_{{\rm{s}}{\rm{i}}{\rm{n}}\omega }$ 和$ \omega \varDelta {\phi }_{{\rm{c}}{\rm{o}}{\rm{s}}\omega } $ 之间的关系(为了方便比较将$ F{\omega }^{2} $ 除以4); (c) 噪声与控制函数的比较, 上图中噪声周期数为1.5, sin类型的噪声积累了最大的相位, cos类型的噪声与自身完全抵消; 下图中噪声周期数为3, 两种类型的噪声都与自身完全抵消Fig. 4. Periodicity of the filter function in the case of a three-level system; (a) Periodic part of
$ F=\dfrac{1}{{\omega }^{2}}16{\rm{s}}{\rm{i}}{\rm{n}}{\left(\dfrac{\omega \tau }{6}\right)}^{4} $ ; (b) relation among$ F{\omega }^{2}, \omega \varDelta {\phi }_{{\rm{s}}{\rm{i}}{\rm{n}}\omega } $ and$ \omega \varDelta {\phi }_{{\rm{c}}{\rm{o}}{\rm{s}}\omega } $ ; (c) comparison between some periods of noise and control function. The number of noise cycles in the upper figure is 1.5. sin-type of noise accumulates a maximum phase, while the cos-type of noise completely cancels out itself. The number of noise cycles in the bottom figure is 3, and both types of noise completely cancel out themselves.
图 6 电荷比特能级与电荷噪声的关系
Fig. 6. Energy levels of a charge qubit as a function of charge noise.
图 7 m不同时, 重复序列下的滤波函数周期性 (a) m = 1; (b) m = 2; (c) m = 3
Fig. 7. Periodicity of filter functions for repeated sequences with different m: (a) m = 1; (b) m = 2; (c) m = 3.
-
[1] Clerk A A, Devoret M H, Girvin S M, Marquardt F, Schoelkopf R J 2010 Rev. Mod. Phys. 82 1155
Google Scholar
[2] Hahn E L 1950 Phys. Rev. 80 580
Google Scholar
[3] Slichter C P 1990 Principles of Nuclear Magnetic Resonance (3rd Ed.) (NewYork: Springer) pp1–7
[4] Viola L, Lloyd S 1998 Phys. Rev. A 58 2733
Google Scholar
[5] Carr H Y, Purcell E M 1954 Phys. Rev. 94 630
Google Scholar
[6] Meiboom S, Gill D 1958 Rev. Sci. Instrum. 29 688
Google Scholar
[7] Grégoire I 2005 Ph. D. Dissertation (Paris: Université Pierre et Marie Curie - Paris VI)
[8] Khodjasteh K, Lidar D A 2005 Phys. Rev. Lett. 95 180501
Google Scholar
[9] Khodjasteh K, Lidar D A 2007 Phys. Rev. A 75 062310
Google Scholar
[10] Uhrig G S 2007 Phys. Rev. Lett. 98 100504
Google Scholar
[11] Uhrig G S 2009 Phys. Rev. Lett. 102 120502
Google Scholar
[12] Uhrig G S 2008 New J. Phys. 10 083024
Google Scholar
[13] Uhrig G S, Pasini S 2010 New J. Phys. 12 045001
Google Scholar
[14] Bylander J, Gustavsson S, Yan F, Yoshihara F, Harrabi K, Fitch G, Oliver W D 2011 Nat. Phys. 7 565
Google Scholar
[15] Gustavsson S, Bylander J, Yan F, Forn-Díaz P, Bolkhovsky V, Braje D, Oliver W D 2012 Phys, Rev. Lett. 108 170503
Google Scholar
[16] Qiu J, Zhou Y, Hu C K, Yuan J, Zhang L, Chu J, Huang W, Liu W, Luo K, Ni Z, Pan X, Yu D 2021 Phys. Rev. A 16 054047
Google Scholar
[17] Google 2023 Nature 614 676
Google Scholar
[18] Gottesman D 1999 Chaos Solitons Fractals 10 1749
Google Scholar
[19] Grassl M, Rötteler M, Beth T 2003 Inter. J. Foundat. Compu. Sci. 14 757
Google Scholar
[20] Bullock S S, OLeary D P, Brennen G K 2005 Phys. Rev. Lett. 94 230502
Google Scholar
[21] Campbell E T, Anwar H, Browne D E 2012 Phys. Rev. X 2 041021
Google Scholar
[22] Campbell E T 2014 Phys. Rev. Lett. 113 230501
Google Scholar
[23] Anwar H, Brown B J, Campbell E T, Browne D E 2014 New J. Phys. 16 063038
Google Scholar
[24] Krishna A, Tillich J P 2019 Phys. Rev. Lett. 123 070507
Google Scholar
[25] Chu J, He X, Zhou Y, Yuan J, Zhang L, Guo Q, Hai Y, Han Z, Hu C K, Huang W, Jia H, Yu D 2023 Nat. Phys. 19 126
Google Scholar
[26] Luo K, Huang W, Tao Z, Zhang L, Zhou Y, Chu J, Liu W, Wang B, Cui J, Liu S, Yan F, Yu D 2023 Phys. Rev. Lett. 130 030603
Google Scholar
[27] Blok M S, Ramasesh V V, Schuster T, O’Brien K, Kreikebaum J M, Dahlen D, Morvan A, Yoshida B, Yao N Y, Siddiqi I 2021 Phys. Rev. X 11 021010
Google Scholar
[28] Suslov M V, Lesovik G B, Blatter G 2011 Phys. Rev. A 83 052317
Google Scholar
[29] Bouchard F, Fickler R, Boyd R W, Karimi E 2017 Sci. Adv. 3 e1601915
Google Scholar
[30] Napolitano R J, Fanchini F F, da Silva A H, Bellomo B 2021 Phys. Rev. Research 3 013235
Google Scholar
[31] Mukhtar M, Saw T B, Soh W T, Gong J 2010 Phys. Rev. A 81 012331
Google Scholar
[32] Koch J, Terri M Y, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys, Rev. A 76 042319
Google Scholar
下载:
计量
- 文章访问数: 4143
- PDF下载量: 199
- 被引次数: 0
