-
弛豫铁电体材料在通讯、传感、超声、能量转换、航空航天等领域具有重要的应用. 与正常铁电体不同, 弛豫铁电体在冷却过程中出现弥散相变, 体系的宏观极化不会突然产生, 而是出现纳米极性微区, 体系的宏观晶体对称性没有明显的变化. 如何理解弥散相变及其与内部机制之间的相互影响是一个重要的问题. 本研究基于伊辛模型(Ising model), 对自旋变量(在研究中视为电偶极子)引入能量势阱的作用, 并计算了这一系统的相变过程. 结果表明这一改进的伊辛模型使极化率的相变曲线显著变缓, 呈现出具有弥散相变的弛豫体特性. 研究显示, 弛豫体现象出现的一个重要原因是系统内部偶极子受到势阱限制而出现反转受阻, 从而使极化率偏离常规铁电体. 利用这一改进的伊辛模型进一步研究了弛豫铁电体的热滞效应, 分析了热滞的起源, 并与实验结果进行了对比分析, 明确了弛豫体弥散相变和热滞的物理机制.
Relaxor ferroelectric is a very special type of ferroelectric material, which has important applications in communication, sensor, ultrasound, energy conversion, and aerospace industry. Unlike normal ferroelectric, a relaxor undergoes a diffuse phase transition in the cooling process, and its macroscopic polarization does not occur suddenly, but polar nano region appears while the macro-symmetry does not change significantly. As the transition from the paraelecric to the ferroelectric phase is a gradual process with a broad dielectric peak, relaxor ferroelectric has no definite Curie temperature (TC), and the temperature corresponding to the maximum dielectric constant (Tm) and the Burns temperature (TB) are often used as their characteristic temperatures. Here, in order to understand the diffuse phase transition and its internal mechanism, we build a modified Ising model by introducing an energy potential well that affects the spin variable (which is regarded as electric dipole in this research) and simulate the phase transition process using this model, which results in significantly smoothed phase transition with respect to temperature, exhibiting relaxor characteristics with diffuse phase transitions. More precisely, it is found that by applying the energy potential well to the dipoles in the system, the ferroelectric phase transition can be significantly broadened, that is, a diffused phase transition appears, showing strong relaxation characteristics that, as the temperature gradually increases, the average electric dipole moment does not change abruptly while the peak value of its permittivity decreases with the energy potential well. Moreover, at a temperature much higher than the transition temperature of the usual Ising model, the system can still maintain a certain polarization, which is in line with relaxor characteristics. By comparing to a previously proposed statistical model, it is found that the relaxation phenomenon is due to the fact that dipoles in the system are constrained by the given potential well, therefore difficult to flip, making the overall polarizability deviate from that of conventional ferroelectrics. Our results therefore show that the existence of dipole energy potential well is an important factor in the relaxation phenomenon of ferroelectric. This modified Ising model, which accounts for the constrained dipoles statistically, is then used to investigate the thermal hysteresis effect of relaxor ferroelectrics in order to understand its origin. By comparing to experimental results, we are able to clarify the physics of the thermal hysteresis of relaxor ferroelectric, deepening our understanding from the theoretical and simulation perspective. [1] Park S E, Shrout T R 1997 J. Appl. Phys. 82 1804
Google Scholar
[2] Service R F 1997 Science 275 1878
Google Scholar
[3] Zhang S J, Li F 2012 J. Appl. Phys. 111 031301
Google Scholar
[4] Bokov A A, Maglione M, Ye Z G 2007 J. Phys. Condens. Matter 19 092001
Google Scholar
[5] Fu H X, Cohen R E 2000 Nature 403 281
Google Scholar
[6] Zhang S J, Li F, Jiang X N, Kim J, Luo J, Geng X C 2015 Prog. Mater. Sci. 68 1
Google Scholar
[7] Sun E W, Cao W W 2014 Prog. Mater. Sci. 65 124
Google Scholar
[8] Ye Z G 2009 MRS Bull. 34 277
Google Scholar
[9] Liu J, Li F, Zeng Y, Jiang Z, Liu L, Wang D, Ye Z G, Jia C L 2017 Phys. Rev. B 96 054115
Google Scholar
[10] Colla E V, Koroleva E Y, Okuneva N M, Vakhrushev S B 1992 J. Phys. Condens. Matter 4 3671
Google Scholar
[11] Manley M E, Lynn J W, Abernathy D L, Specht E D, Delaire O, Bishop A R, Sahul R, Budai J D 2014 Nat. Commun. 5 3683
Google Scholar
[12] Wang D, Bokov A A, Ye Z G, Hlinka J, Bellaiche L 2016 Nat. Commun. 7 11014
Google Scholar
[13] Sherrington D 2013 Phys. Rev. Lett. 111 227601
Google Scholar
[14] Sherrington D 2014 Phys. Rev. B 89 064105
Google Scholar
[15] Noheda B 2002 Curr. Opin. Solid State Mater. Sci. 6 27
Google Scholar
[16] Jin Y M, Wang Y U, Khachaturyan A G, Li J F, Viehland D 2003 Phys. Rev. Lett. 91 197601
Google Scholar
[17] Kleemann W 2014 Phys. Status Solidi B 251 1993
Google Scholar
[18] Jeong I K, Darling T W, Lee J K, Proffen T, Heffner R H, Park J S, Hong K S, Dmowski W, Egami T 2005 Phys. Rev. Lett. 94 147602
Google Scholar
[19] Hiraka H, Lee S H, Gehring P M, Xu G Y, Shirane G 2004 Phys. Rev. B 70 184105
Google Scholar
[20] Xie L, Li Y L, Yu R, Cheng Z Y, Wei X Y, Yao X, Jia C L, Urban K, Bokov A A, Ye Z G, Zhu J 2012 Phys. Rev. B 85 014118
Google Scholar
[21] Akbarzadeh A R, Prosandeev S, Walter E J, Al-Barakaty A, Bellaiche L 2012 Phys. Rev. Lett. 108 257601
Google Scholar
[22] Xu G, Wen J, Stock C, Gehring P M 2008 Nat. Mater. 7 562
Google Scholar
[23] Manley M E, Abernathy D L, Sahul R, Parshall D E, Lynn J W, Christianson A D, Stonaha P J, Specht E D, Budai J D 2016 Sci. Adv. 2 1501814
Google Scholar
[24] Li F, Zhang S J, Yang T N, Xu Z, Zhang N, Liu G, Wang J J, Wang J L, Cheng Z X, Ye Z G, Luo J, Shrout T R, Chen L Q 2016 Nat. Commun. 7 13807
Google Scholar
[25] Tinte S, Burton B P, Cockayne E, Waghmare U V 2006 Phys. Rev. Lett. 97 137601
Google Scholar
[26] Pasciak M, Welberry T R, Kulda J, Kempa M, Hlinka J 2012 Phys. Rev. B 85 224109
Google Scholar
[27] Takenaka H, Grinberg I, Rappe A M 2013 Phys. Rev. Lett. 110 147602
Google Scholar
[28] Grinberg I, Shin Y H, Rappe A M 2009 Phys. Rev. Lett. 103 197601
Google Scholar
[29] Sepliarsky M, Cohen R E 2011 J. Phys.Condens. Matter 23 435902
Google Scholar
[30] Adam L, Tsuyoshi H, Dorota L 1995 Phys. Rev. Lett. 74 3888
Google Scholar
[31] Newman M E J, Barkema G T 1999 Monte Carlo Methods in Statistical Physics (Oxford: Oxford University Press) p17
[32] Liu L, Ren S, Zhang J, Peng B, Fang L, Wang D 2018 J. Am. Ceram. Soc. 101 2408
Google Scholar
[33] Prosandeev S, Wang D, Akbarzadeh A R, Bellaiche L 2015 J. Phys.Condens. Matter 27 223202
Google Scholar
[34] Prosandeev S, Wang D, Akbarzadeh A, Dkhil B, Bellaiche L 2013 Phys. Rev. Lett. 110 207601
Google Scholar
[35] Liu Y, Phillips L C, Mattana R, Bibes M, Barthelemy A, Dkhil B 2016 Nat. Commun. 7 11614
Google Scholar
[36] Moya X, Kar-Narayan S, Mathur N D 2014 Nat. Mater. 13 439
Google Scholar
[37] Burns G, Dacol F H 1983 Phys. Rev. B 28 2527
Google Scholar
[38] Liu Y, Haibibu A, Xu W H, Han Z B, Wang Q 2020 Adv. Funct. Mater. 30 2000648
Google Scholar
[39] Westphal V, Kleemann W, Glinchuk M D 1992 Phys. Rev. Lett. 68 847
Google Scholar
-
图 1 平均电偶极矩随温度的变化 (a) 初始态为极化状态的升温过程; (b) 初始态随机状态的降温过程
Fig. 1. Temperature dependence of the average electric dipole moment: (a) Heating process from the initial state with all dipoles being +1; (b) cooling process from the initial state with random dipoles.
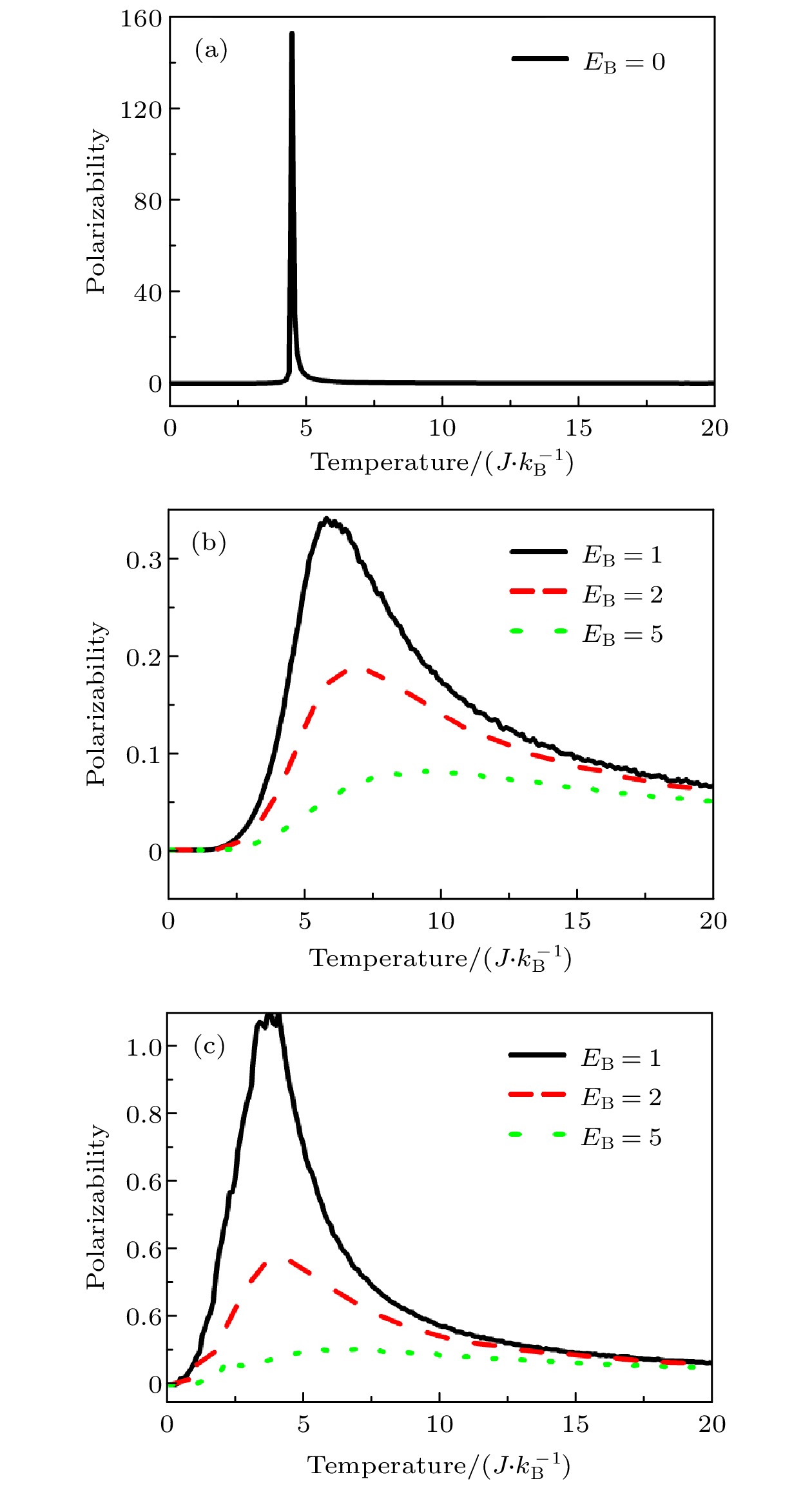
图 2 不同能量势阱下电极化率随温度的变化 (a) 无能量势阱, 初始态为极化态的升温过程; (b) 存在能量势阱, 初始态为极化态的升温过程; (c) 存在能量势阱, 初始态为随机态的降温过程
Fig. 2. Polarizability versus temperature with different
$ {E}_{\mathrm{B}}: $ (a) Heating process from an initial state with all dipoles being +1 for EB = 0; (b) heating process from an initial state with all dipoles being +1 with nonzero EB; (c) cooling process from an initial state with random dipoles with nonzero EB 
图 4 升温和降温过程极化率随温度变化的对比
Fig. 4. Polarizability as a function of temperature in heating/cooling processes.
图 5
$ {E}_{\mathrm{B}}=0.5 $ 时, 不同过程中平均电偶极矩 (a) 极化率(b)随温度变化的对比Fig. 5. Average electric dipole moments (a) and polarizability (b) as functions of temperature during different processes for
$ {E}_{\mathrm{B}}=0.5 $ .$ {E}_{\mathrm{B}} $
(设置值)$ {\chi }_{1} $ $ \gamma $ $ \theta $ $ {E}_{\mathrm{B}} $
(拟合值)$ {\chi }_{2} $ $ {T}_{\mathrm{O}} $ 升温
过程1 2.200 1.78 1.899 2.314 0 2.681 2 0.653 1.40 3.169 2.653 0 3.092 5 0.299 1.39 6.080 6.915 0 2.408 降温
过程1 1.67 1.490 1.65 2.660 0 3.537 2 0.63 1.354 3.07 3.400 0 3.621 5 0.16 1.740 11.32 4.280 0 2.290 
下载: 导出CSV
-
[1] Park S E, Shrout T R 1997 J. Appl. Phys. 82 1804
Google Scholar
[2] Service R F 1997 Science 275 1878
Google Scholar
[3] Zhang S J, Li F 2012 J. Appl. Phys. 111 031301
Google Scholar
[4] Bokov A A, Maglione M, Ye Z G 2007 J. Phys. Condens. Matter 19 092001
Google Scholar
[5] Fu H X, Cohen R E 2000 Nature 403 281
Google Scholar
[6] Zhang S J, Li F, Jiang X N, Kim J, Luo J, Geng X C 2015 Prog. Mater. Sci. 68 1
Google Scholar
[7] Sun E W, Cao W W 2014 Prog. Mater. Sci. 65 124
Google Scholar
[8] Ye Z G 2009 MRS Bull. 34 277
Google Scholar
[9] Liu J, Li F, Zeng Y, Jiang Z, Liu L, Wang D, Ye Z G, Jia C L 2017 Phys. Rev. B 96 054115
Google Scholar
[10] Colla E V, Koroleva E Y, Okuneva N M, Vakhrushev S B 1992 J. Phys. Condens. Matter 4 3671
Google Scholar
[11] Manley M E, Lynn J W, Abernathy D L, Specht E D, Delaire O, Bishop A R, Sahul R, Budai J D 2014 Nat. Commun. 5 3683
Google Scholar
[12] Wang D, Bokov A A, Ye Z G, Hlinka J, Bellaiche L 2016 Nat. Commun. 7 11014
Google Scholar
[13] Sherrington D 2013 Phys. Rev. Lett. 111 227601
Google Scholar
[14] Sherrington D 2014 Phys. Rev. B 89 064105
Google Scholar
[15] Noheda B 2002 Curr. Opin. Solid State Mater. Sci. 6 27
Google Scholar
[16] Jin Y M, Wang Y U, Khachaturyan A G, Li J F, Viehland D 2003 Phys. Rev. Lett. 91 197601
Google Scholar
[17] Kleemann W 2014 Phys. Status Solidi B 251 1993
Google Scholar
[18] Jeong I K, Darling T W, Lee J K, Proffen T, Heffner R H, Park J S, Hong K S, Dmowski W, Egami T 2005 Phys. Rev. Lett. 94 147602
Google Scholar
[19] Hiraka H, Lee S H, Gehring P M, Xu G Y, Shirane G 2004 Phys. Rev. B 70 184105
Google Scholar
[20] Xie L, Li Y L, Yu R, Cheng Z Y, Wei X Y, Yao X, Jia C L, Urban K, Bokov A A, Ye Z G, Zhu J 2012 Phys. Rev. B 85 014118
Google Scholar
[21] Akbarzadeh A R, Prosandeev S, Walter E J, Al-Barakaty A, Bellaiche L 2012 Phys. Rev. Lett. 108 257601
Google Scholar
[22] Xu G, Wen J, Stock C, Gehring P M 2008 Nat. Mater. 7 562
Google Scholar
[23] Manley M E, Abernathy D L, Sahul R, Parshall D E, Lynn J W, Christianson A D, Stonaha P J, Specht E D, Budai J D 2016 Sci. Adv. 2 1501814
Google Scholar
[24] Li F, Zhang S J, Yang T N, Xu Z, Zhang N, Liu G, Wang J J, Wang J L, Cheng Z X, Ye Z G, Luo J, Shrout T R, Chen L Q 2016 Nat. Commun. 7 13807
Google Scholar
[25] Tinte S, Burton B P, Cockayne E, Waghmare U V 2006 Phys. Rev. Lett. 97 137601
Google Scholar
[26] Pasciak M, Welberry T R, Kulda J, Kempa M, Hlinka J 2012 Phys. Rev. B 85 224109
Google Scholar
[27] Takenaka H, Grinberg I, Rappe A M 2013 Phys. Rev. Lett. 110 147602
Google Scholar
[28] Grinberg I, Shin Y H, Rappe A M 2009 Phys. Rev. Lett. 103 197601
Google Scholar
[29] Sepliarsky M, Cohen R E 2011 J. Phys.Condens. Matter 23 435902
Google Scholar
[30] Adam L, Tsuyoshi H, Dorota L 1995 Phys. Rev. Lett. 74 3888
Google Scholar
[31] Newman M E J, Barkema G T 1999 Monte Carlo Methods in Statistical Physics (Oxford: Oxford University Press) p17
[32] Liu L, Ren S, Zhang J, Peng B, Fang L, Wang D 2018 J. Am. Ceram. Soc. 101 2408
Google Scholar
[33] Prosandeev S, Wang D, Akbarzadeh A R, Bellaiche L 2015 J. Phys.Condens. Matter 27 223202
Google Scholar
[34] Prosandeev S, Wang D, Akbarzadeh A, Dkhil B, Bellaiche L 2013 Phys. Rev. Lett. 110 207601
Google Scholar
[35] Liu Y, Phillips L C, Mattana R, Bibes M, Barthelemy A, Dkhil B 2016 Nat. Commun. 7 11614
Google Scholar
[36] Moya X, Kar-Narayan S, Mathur N D 2014 Nat. Mater. 13 439
Google Scholar
[37] Burns G, Dacol F H 1983 Phys. Rev. B 28 2527
Google Scholar
[38] Liu Y, Haibibu A, Xu W H, Han Z B, Wang Q 2020 Adv. Funct. Mater. 30 2000648
Google Scholar
[39] Westphal V, Kleemann W, Glinchuk M D 1992 Phys. Rev. Lett. 68 847
Google Scholar
下载:
计量
- 文章访问数: 6834
- PDF下载量: 168
- 被引次数: 0
