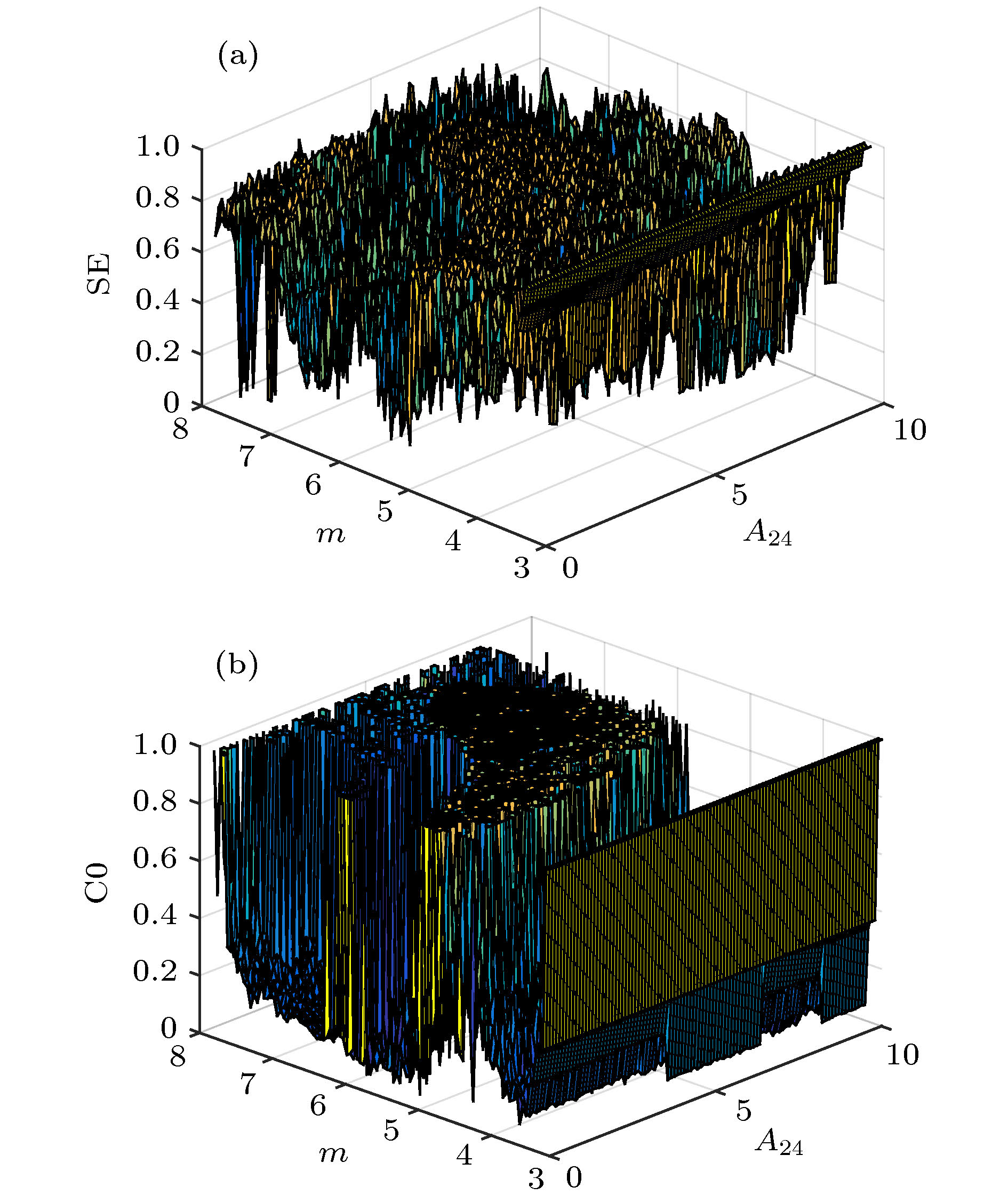
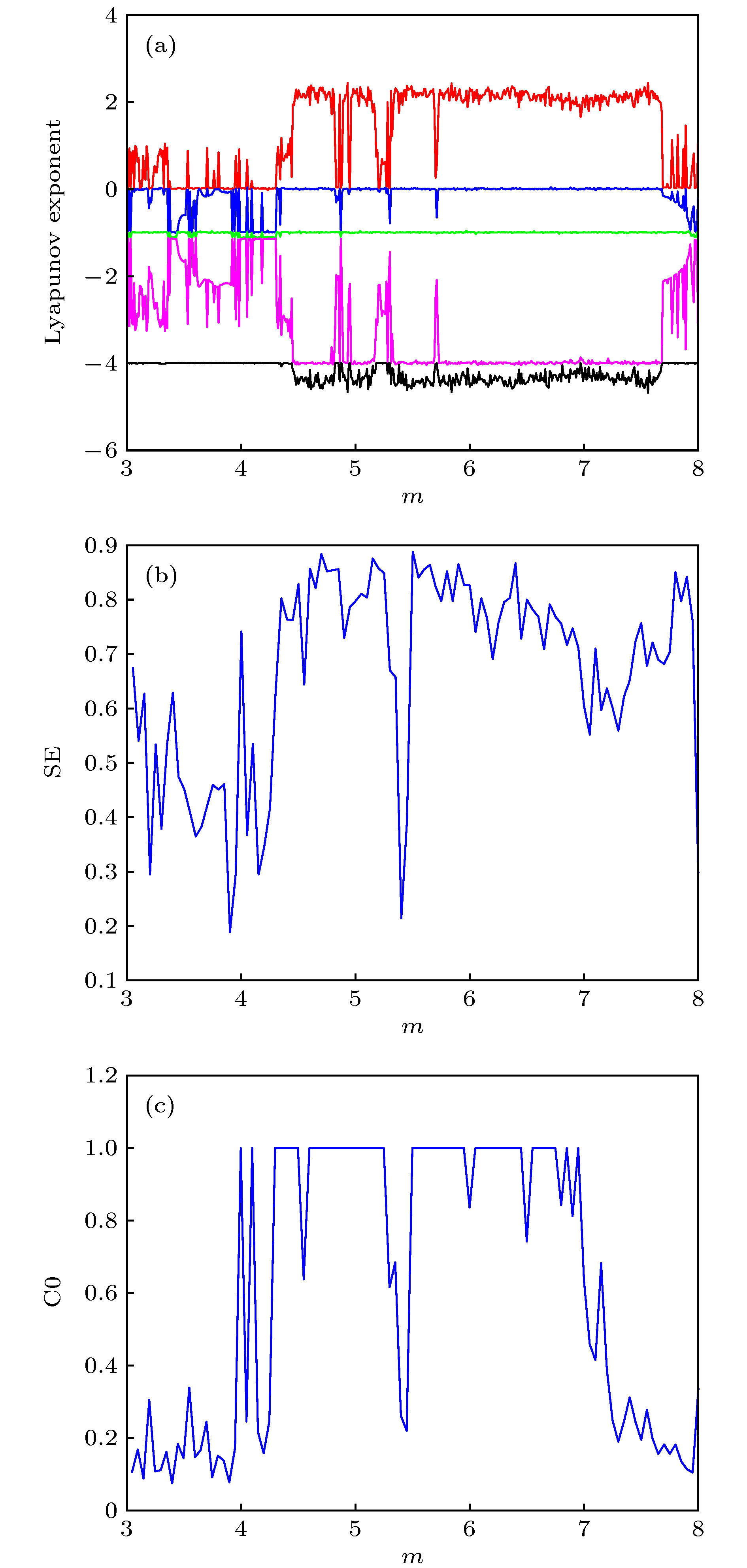
-
大量动物实验表明, 生物神经系统中存在着不规则的混沌现象. 混沌神经网络是一种高度非线性动力系统, 它可以实现一系列复杂的动力学行为, 能够优化全局搜索和神经计算, 还可产生伪随机序列进行信息加密. 基于脑波由不同频率的正弦信号叠加理论, 为使神经网络更具生物特性, 提出了一种基于多频-变频正弦函数和分段型函数的非单调激活函数. 分析表明, 通过调节参数可使该激活函数拥有不同状态的脑电信号, 能够模拟频率不同、类型不同的脑电波同时工作时丰富多变的脑部活动. 基于该激活函数设计了一种新型混沌细胞神经网络. 采用基于结构复杂度的SE复杂度算法和C0复杂度算法分析了神经网络的复杂度; 利用Lyapunov指数谱、分岔图和吸引盆等方法, 详细分析了激活函数参数变化对其动力学特性的影响, 发现此混沌神经网络模型出现了一系列的复杂现象, 如多种不同类型的混沌吸引子、共存混沌吸引子、共存极限环等, 提升了混沌神经网络的性能, 证明了多频正弦混沌神经网络具有丰富的动力学特性, 使得其在信息处理、信息加密等方面也具有较好的前景.A large number of animal experiments show that there is irregular chaos in the biological nervous systems. An artificial chaotic neural network is a highly nonlinear dynamic system, which can realize a series of complex dynamic behaviors, optimize global search and neural computation, and generate pseudo-random sequences for information encryption. According to the superposition theory of sinusoidal signals with different frequencies of brain waves, a non-monotone activation function based on the multifrequency-frequency conversion sinusoidal function and a piecewise function is proposed to make a neural network more consistent with the biological characteristics. The analysis shows that by adjusting the parameters, the activation function can exhibit the EEG signals in its different states, which can simulate the rich and varying brain activities when the brain waves of different frequencies and types work at the same time. According to the activation function we design a new chaotic cellular neural network. The complexity of the chaotic neural network is analyzed by the structural complexity based SE algorithm and C0 algorithm. By means of Lyapunov exponential spectrum, bifurcation diagram and basin of attraction, the effects of the activation function’s parameters on its dynamic characteristics are analyzed in detail, and it is found that a series of complex phenomena appears in the chaotic neural network, such as many different types of chaotic attractors, coexistent chaotic attractors and coexistence limit cycles, which improves the performance of the chaotic neural network, and proves that the multi-frequency sinusoidal chaotic neural network has rich dynamic characteristics, so it has a good prospect in information processing, information encryption and other aspects.
[1] 孙为民, 王晖, 高涛 2017 电子世界 24 27
Google Scholar
Sun W M, Wang H, Gao T, Xia R R, Zhang L 2017 Elec. World. 24 27
Google Scholar
[2] Wang X Y, Li Z M 2019 Optlase. Eng. 115 107
[3] 董哲康, 杜晨杰, 林辉品, 赖俊昇, 胡小方, 段书凯 2020 电子与信息学报 42 835
Google Scholar
Dong Z K, Du C J, Lin H P, Lai J S, Hu X F, Duan S K 2020 J. Elec. Inform. Tech. 42 835
Google Scholar
[4] Bao H, Hu A H, Liu W B, Bao B C 2019 IEEE Trans. Neural. Netw. Learn. Syst. 31 502
Google Scholar
[5] 王春华, 蔺海荣, 孙晶如, 周玲, 周超, 邓全利 2020 电子与信息学报 42 795
Google Scholar
Wang C H, Lin H R, Sun R J, Zhou L, Zhou C, Deng Q L 2020 J. Elec. Inform. Tech. 42 795
Google Scholar
[6] Freeman W J 1987 Biol. Cybern. 56 139
Google Scholar
[7] Chua L O, Yang L 1988 IEEE T Circuits 35 1257
Google Scholar
[8] Aihara K, Takabe T, Toyoda M 1990 Phys. Lett. A 144 333
Google Scholar
[9] Chen L P, Hao Y, Huang T W, Yuan L G, Zheng S, Yin L S 2020 Neural Networks 125 174
Google Scholar
[10] Jiang C S, Chen Q 2020 Chaos Soliton Fract. 131 109
[11] Potapov A, Ali M K 2000 Phys. Lett. A 277 310
Google Scholar
[12] Yi Z, Xu G J, Qin X Z, Jia Z H 2011 Proc. Eng. 24 479
Google Scholar
[13] Zhang J H, Xu Y Q 2009 Nat. Sci. 1 204
Google Scholar
[14] Sih G C, Tang K K 2012 Theor. Appl. Fract. Mec. 61 21
Google Scholar
[15] 胡志强, 李文静, 乔俊飞 2016 66 090502
Google Scholar
Hu Z Q, Li W J, Qiao J F 2016 Acta Phys. Sin. 66 090502
Google Scholar
[16] Sanei S, Chambers J A 2007 Comput. Intel. Neurosc. 2 1178
[17] 殷艳红 2008 硕士学位论文 (上海: 同济大学)
Yin Y H 2008 M. S. Thesis (Shanghai: Tongji University) (in Chinese)
[18] Pedro J C, De Carvalho N B 1999 IEEE Trans. Microw. Theory Tech. 47 2393
Google Scholar
[19] Hajji R, Beanregard F, Ghannouchi F M 1997 IEEE Trans. Microw Theory Tech. 45 1093
Google Scholar
[20] Jan V, Frans V, Marc B V 2000 56th ARFTG Conference Digest Boulder, AZ, USA, November 30−December 1, 2000 p1
[21] Gulcehre C, Moczulski M, Denil M, Bengio Y 2017 International Joint Conference on Neural Networks Anchorage, AK, USA, May 14–19, 2017 p17010846
[22] Phillip P A, Chiu F L, Nick S J 2009 Phys. Rev. Stat. Non. Soft Matter Phys. 79 011915
Google Scholar
[23] Chen F, Xu J H, Gu F J 2000 Biol. Cybern. 83 355
Google Scholar
[24] 孙克辉, 贺少波, 朱从旭, 何毅 2013 电子学报 41 1765
Google Scholar
Sui K H, He S B, Zhu C X, He Y 2013 Acta Elec. Sin. 41 1765
Google Scholar
-
图 3 幅值和频率随q, m, n的变化 (a)幅值A随q的变化; (b)频率1/
${\varepsilon _1}$ 随m的变化; (c)频率1/${\varepsilon _2}$ 随n的变化Fig. 3. Change characteristic of the amplitude and frequency with q, m, n: (a) The change characteristic of the amplitude A with q; (b) the change characteristic of the frequency 1/
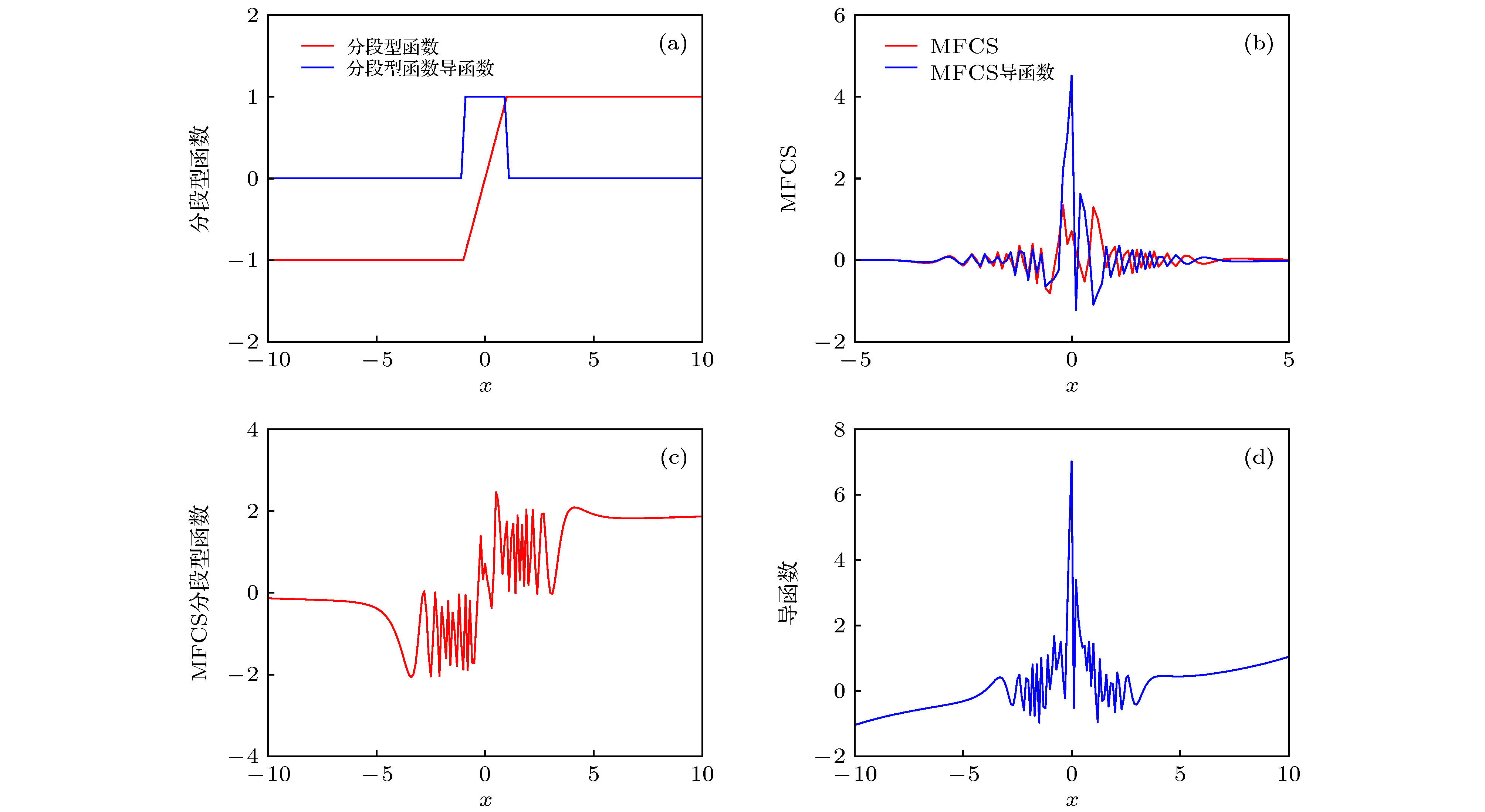
${\varepsilon _1}$ with m; (c) the change characteristic of the frequency 1/${\varepsilon _2}$ with n.
图 5 分段型函数、MFCS和MFCS激活函数及其导数图像 (a)分段型函数及其导函数; (b) MFCS及其导函数; (c) MFCS激活函数; (d) MFCS激活函数导函数.
Fig. 5. Piecewise function, MFCS and MFCS activation function and its derivative image: (a) Piecewise function and its derivative function; (b) MFCS and its derivative function; (c) MFCS activation function; (d) MFCS activation function and its derivative function.
图 7 系统的三维复杂度 (a) SE图; (b) C0图
Fig. 7. Three-dimensional complexity of the system: (a) The complexity of the SE; (b) the complexity of the C0.
图 8 系统的二维复杂度 (a) Lyapunov指数谱; (b) SE图; (c) C0图
Fig. 8. Two-dimensional complexity of the system: (a) Lyapunov exponents; (b) the complexity of SE; (c) the complexity of C0.
图 10 系统随参数n变化的相图 (a) n = 0.2; (b) n = 0.53; (c) n = 0.61; (d) n = 0.7; (e) n = 1.62; (f) n = 2.98; (g) n = 3.16
Fig. 10. Chaotic attractors of the system changing with parameter n: (a) n = 0.2; (b) n = 0.53; (c) n = 0.61; (d) n = 0.7; (e) n = 1.62; (f) n = 2.98; (g) n = 3.16.
图 11 系统随参数c变化的分岔图和Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
Fig. 11. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with c: (a) Bifurcation diagram; (b) Lyapunov exponents.
图 12 系统随参数c变化的相图 (a) c = 0.08; (b) c = 0.118; (c) c = 0.25; (d) c = 0.50; (e) c = 0.52; (f) c = 0.73
Fig. 12. Chaotic attractors of the system changing with parameter c: (a) c = 0.08; (b) c = 0.118; (c) c = 0.25; (d) c = 0.50; (e) c = 0.52; (f) c = 0.73.
图 13 系统随参数q变化的分岔图和Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
Fig. 13. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with q: (a) Bifurcation diagram; (b) Lyapunov exponents.
图 14 系统随参数q变化的相图 (a) q = –1.26; (b) q = –0.75; (c) q = –0.38; (d) q = –0.25
Fig. 14. Chaotic attractors of the system changing with parameter q: (a) q = –1.26; (b) q = –0.75; (c) q = –0.38; (d) q = –0.25.
图 9 系统随参数n变化的分岔图和Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
Fig. 9. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with n: (a) Bifurcation diagram; (b) Lyapunov exponents.
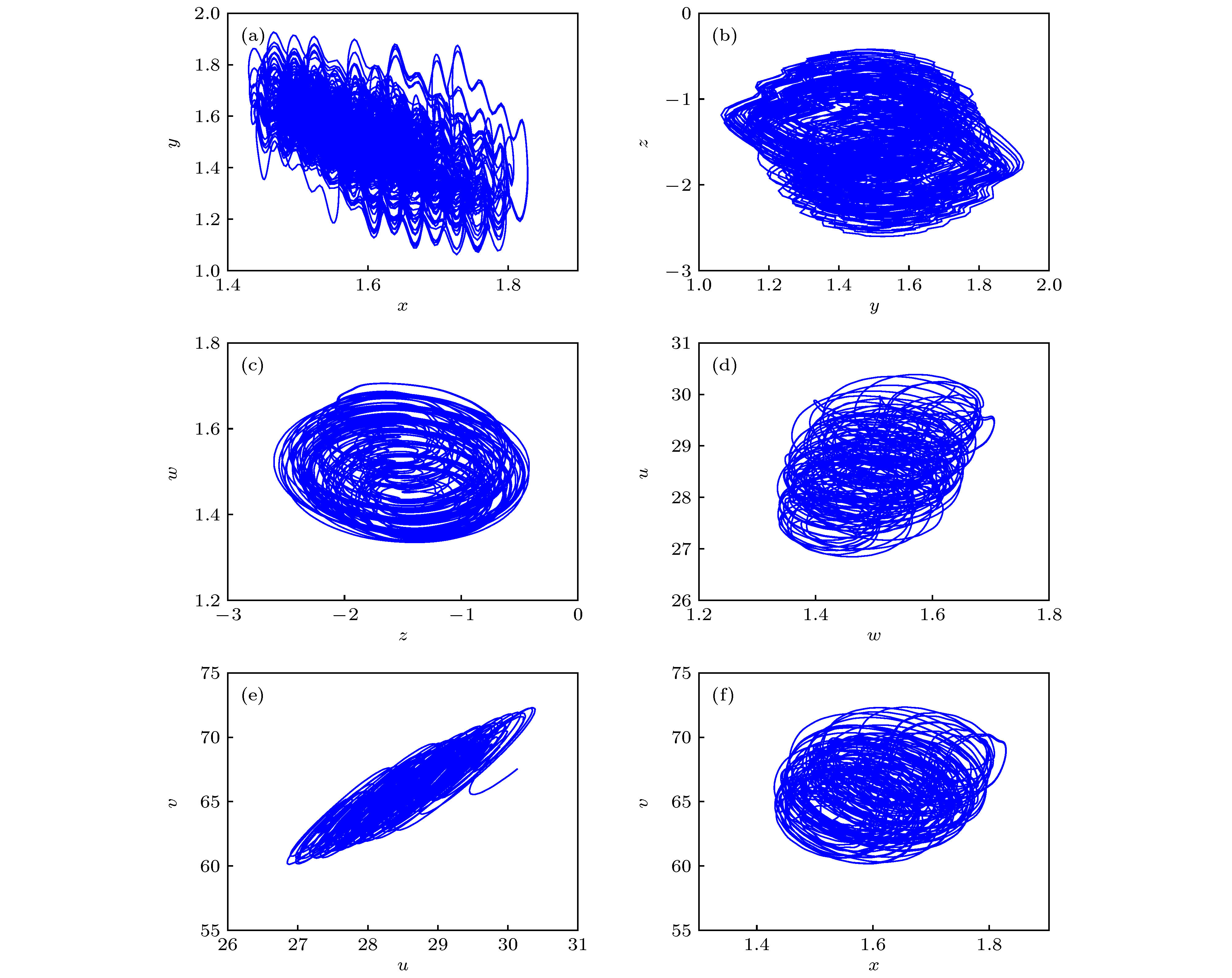
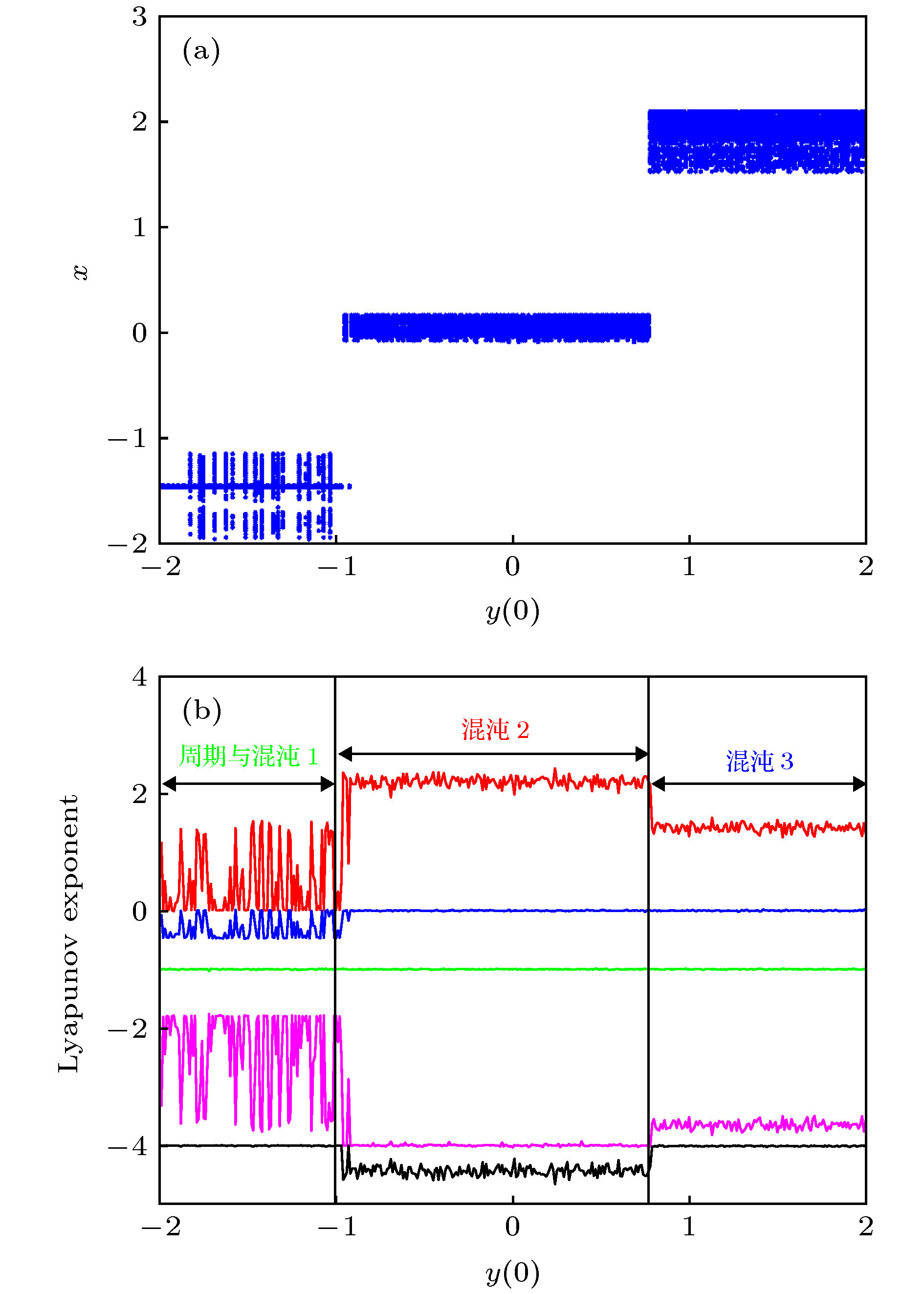
图 15 系统随参数c, q, n变化的几种典型相图 (a) c = 0.25, q = –1, n = 2.5; (b) c = 0.73, q = –1, n = 2.5; (c) c = 0.52, q = –1, n = 2.5; (d) c = 0.25, q =–1, n = 0.715; (e) c = 0.118, q = –1, n = 2.5; (f) c = 0.25, q = –1, n = 0.2; (g) c = 0.73, q = –0.9, n = 2.5; (h) c = 0.25, q = –1, n = 2.98; (i) c = 0.25, q = –1, n = 3.16; (j) c = 0.08, q = –1, n = 2.5; (k) c = –0.25, q = –0.9, n = 2.5; (l) c = 0.25, q = –1, n = 0.61
Fig. 15. Several typical chaotic attractors of the system changing with parameter c, q, n: (a) c = 0.25, q = –1, n = 2.5; (b) c = 0.73, q = –1, n = 2.5; (c) c = 0.52, q = –1, n = 2.5; (d) c = 0.25, q =–1, n = 0.715; (e) c = 0.118, q = –1, n = 2.5; (f) c = 0.25, q = –1, n = 0.2; (g) c = 0.73, q = –0.9, n = 2.5; (h) c = 0.25, q = –1, n = 2.98; (i) c = 0.25, q = –1, n = 3.16; (j) c = 0.08, q = –1, n = 2.5; (k) c = –0.25, q = –0.9, n = 2.5; (l) c = 0.25, q = –1, n = 0.61.
图 16 系统随初始值y(0)变化的分岔图和Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
Fig. 16. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with the initial value y(0): (a) Bifurcation diagram; (b) Lyapunov exponents.
图 17 系统随初始值y(0)变化的相图-共存吸引子
Fig. 17. Chaotic attractors of the system changing with the initial value y(0)-coexistence attractor.
图 18 系统在x-y-z平面的共存吸引子 (a) 混沌吸引子共存; (b) 混沌吸引子与极限环共存; (c) 极限环共存
Fig. 18. Coexistence attractor of the system in the x-y-z plane: (a) Chaotic attractors coexist; (b) chaos attractors coexist with limit cycles; (c) limit cycles coexist.
图 19 系统随x(0), y(0), z(0)变化的吸引盆 (a)系统随x(0), y(0)变化的吸引盆; (b)系统随x(0), z(0)变化的吸引盆
Fig. 19. Suction basin of the system varying with x(0), y(0) and z(0): (a) The suction basin of the system varying with x(0), y(0); (b) the suction basin of the system varying with x(0), z(0).
表 1 频率
${\varepsilon _1}, {\varepsilon _2}$ 随n的变化Table 1. Change characteristic of the frequency
${\varepsilon _1}$ and${\varepsilon _2}$ with n.类型 频率/Hz ${\varepsilon _1}$(0) ${\varepsilon _2}$(0) $\delta $ 0.50—3.01 0.32 0.64 $\theta $ 3.98—6.97 0.04 0.08 $\alpha $ 7.96—15.09 0.02 0.04 $\beta $ 15.92—30.18 0.01 0.02 $\gamma $ 36.17—100.31 0.0044 0.0088 
下载: 导出CSV
参数 参数值 参数 参数值 参数 参数值 参数 参数值 S13 –1.0 S41 98 S65 4.0 m 10.6 S14 –1.0 S44 –105 S66 –4.0 n 0.1 S22 –1.3 S51 1.0 A24 5.0 ${\varepsilon _1}$ 0.04 S23 2.0 S52 18 A 0.5 ${\varepsilon _2} $ 0.02 S31 13.0 S55 –1 c 0.25 φ $ - {{\text{π}} / {{4}}} $ S32 –14.0 S62 100 q –1.0
下载: 导出CSV
表 3 参数c, q, n取不同值时, 其他参数的取值
Table 3. Values of other parameters when changing c, q, n.
参数 参数值 参数 参数值 A24 5 ${\varepsilon _1}$ 0.04 A 0.5 ${\varepsilon _2}$ 0.02 m 10.6 φ $ - {{\text{π}} / {\rm{4}}}$
下载: 导出CSV
参数 参数值 参数 参数值 A24 5 q –1 A 0.5 ${\varepsilon _1}$ 0.04 m 5.6 ${\varepsilon _2}$ 0.02 n 2.5 φ $ - {{\text{π}} / {\rm{4}}}$
下载: 导出CSV
表 5 初始条件的取值
Table 5. Values of initial conditions.
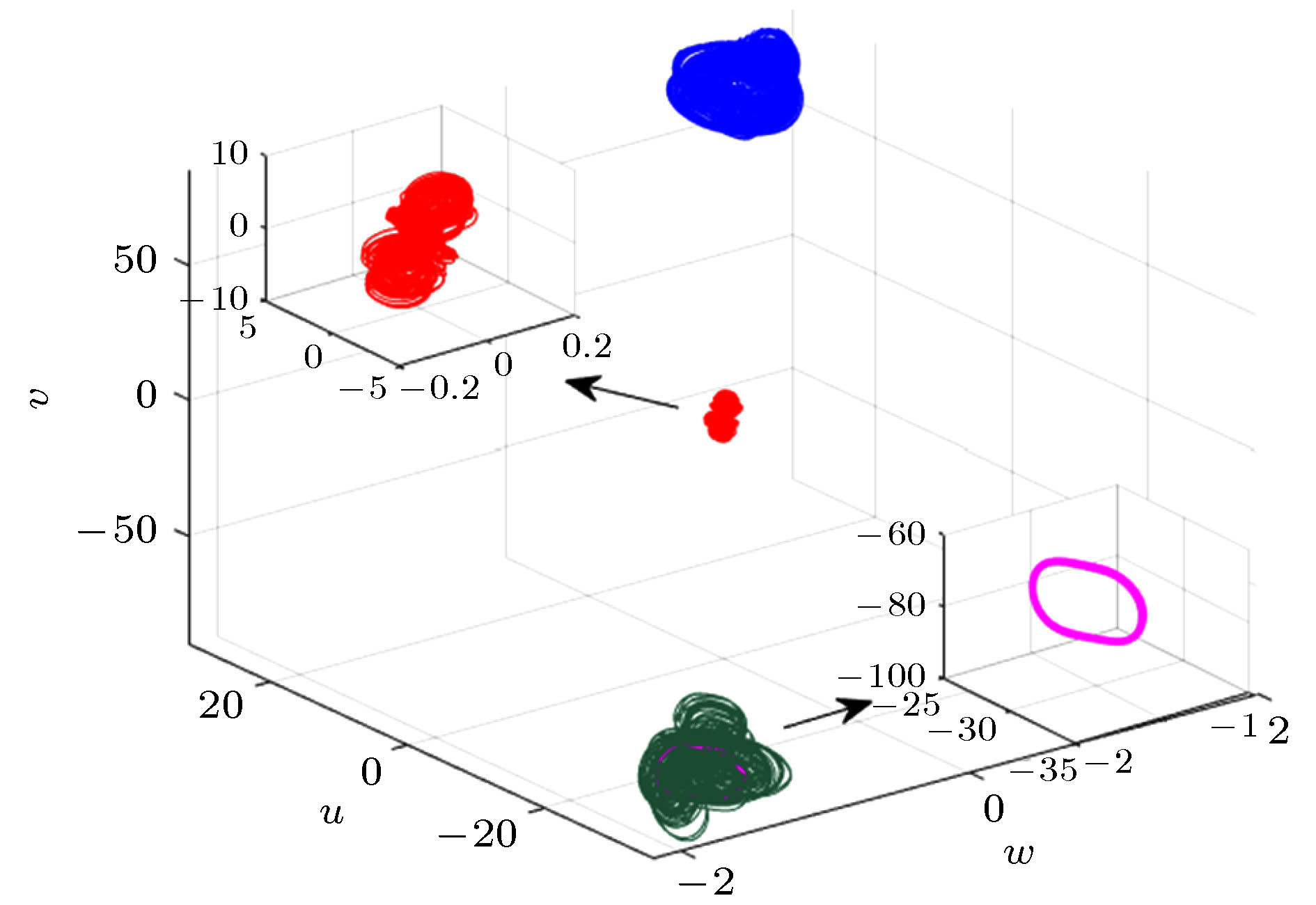
性质 类型 初始条件 混沌吸引子与
混沌吸引子Ic型、
IIc型(0.2, 0.2, 0.3, 0.4, 0.5, 0.6),
(0.52, 0.2, 0.3, 0.4, 0.5, 0.6)Ic型、
IIIc型(0.2, 0.2, 0.3, 0.4, 0.5, 0.6),
(–0.5, –1.2, 0.3, 0.4, 0.5, 0.6)IIc型、IIIc型 (0.52, 0.2, 0.3, 0.4, 0.5, 0.6),
(–0.5, –1.2, 0.3, 0.4, 0.5, 0.6)混沌吸引子
与极限环IIc型、Ip型 (0.82, 1.5, 0.3, 0.4, 0.5, 0.6),
(5.5, 5.81, 0.305, 0.4, 0.5, 0.6001)IIIc型、IIp型 (–0.8, –1.5, 0.3, 0.4, 0.5, 0.6),
(0.1, –1.51, 0.3, 0.4, 0.5, 0.6)极限环与
极限环Ip型、IIp型 (5.5, 5.81, 0.305, 0.4, 0.5, 0.6001),
(0.1, –1.51, 0.3, 0.4, 0.5, 0.6)
下载: 导出CSV
-
[1] 孙为民, 王晖, 高涛 2017 电子世界 24 27
Google Scholar
Sun W M, Wang H, Gao T, Xia R R, Zhang L 2017 Elec. World. 24 27
Google Scholar
[2] Wang X Y, Li Z M 2019 Optlase. Eng. 115 107
[3] 董哲康, 杜晨杰, 林辉品, 赖俊昇, 胡小方, 段书凯 2020 电子与信息学报 42 835
Google Scholar
Dong Z K, Du C J, Lin H P, Lai J S, Hu X F, Duan S K 2020 J. Elec. Inform. Tech. 42 835
Google Scholar
[4] Bao H, Hu A H, Liu W B, Bao B C 2019 IEEE Trans. Neural. Netw. Learn. Syst. 31 502
Google Scholar
[5] 王春华, 蔺海荣, 孙晶如, 周玲, 周超, 邓全利 2020 电子与信息学报 42 795
Google Scholar
Wang C H, Lin H R, Sun R J, Zhou L, Zhou C, Deng Q L 2020 J. Elec. Inform. Tech. 42 795
Google Scholar
[6] Freeman W J 1987 Biol. Cybern. 56 139
Google Scholar
[7] Chua L O, Yang L 1988 IEEE T Circuits 35 1257
Google Scholar
[8] Aihara K, Takabe T, Toyoda M 1990 Phys. Lett. A 144 333
Google Scholar
[9] Chen L P, Hao Y, Huang T W, Yuan L G, Zheng S, Yin L S 2020 Neural Networks 125 174
Google Scholar
[10] Jiang C S, Chen Q 2020 Chaos Soliton Fract. 131 109
[11] Potapov A, Ali M K 2000 Phys. Lett. A 277 310
Google Scholar
[12] Yi Z, Xu G J, Qin X Z, Jia Z H 2011 Proc. Eng. 24 479
Google Scholar
[13] Zhang J H, Xu Y Q 2009 Nat. Sci. 1 204
Google Scholar
[14] Sih G C, Tang K K 2012 Theor. Appl. Fract. Mec. 61 21
Google Scholar
[15] 胡志强, 李文静, 乔俊飞 2016 66 090502
Google Scholar
Hu Z Q, Li W J, Qiao J F 2016 Acta Phys. Sin. 66 090502
Google Scholar
[16] Sanei S, Chambers J A 2007 Comput. Intel. Neurosc. 2 1178
[17] 殷艳红 2008 硕士学位论文 (上海: 同济大学)
Yin Y H 2008 M. S. Thesis (Shanghai: Tongji University) (in Chinese)
[18] Pedro J C, De Carvalho N B 1999 IEEE Trans. Microw. Theory Tech. 47 2393
Google Scholar
[19] Hajji R, Beanregard F, Ghannouchi F M 1997 IEEE Trans. Microw Theory Tech. 45 1093
Google Scholar
[20] Jan V, Frans V, Marc B V 2000 56th ARFTG Conference Digest Boulder, AZ, USA, November 30−December 1, 2000 p1
[21] Gulcehre C, Moczulski M, Denil M, Bengio Y 2017 International Joint Conference on Neural Networks Anchorage, AK, USA, May 14–19, 2017 p17010846
[22] Phillip P A, Chiu F L, Nick S J 2009 Phys. Rev. Stat. Non. Soft Matter Phys. 79 011915
Google Scholar
[23] Chen F, Xu J H, Gu F J 2000 Biol. Cybern. 83 355
Google Scholar
[24] 孙克辉, 贺少波, 朱从旭, 何毅 2013 电子学报 41 1765
Google Scholar
Sui K H, He S B, Zhu C X, He Y 2013 Acta Elec. Sin. 41 1765
Google Scholar
下载:
计量
- 文章访问数: 7150
- PDF下载量: 165
- 被引次数: 0
