改进分析型嵌入原子法在W(100)表面声子谱中的应用

张晓军; 王安祥; 严祥安; 陈长乐

doi:10.7498/aps.69.20191910

摘要

在表面晶格动力学理论的框架下, 采用改进分析型嵌入原子法模型模拟W(100)表面沿$\bar \varGamma \bar L$、$\bar L\bar M$和$\bar \Gamma \bar M$对称方向上的声子色散频谱, 并计算不同对称点处的极化矢量. 按照表面模的判定依据和标记方法绘制不同对称方向上的表面模, 并讨论表面模的分布范围和模式耦合现象. 基于计算所得的极化矢量, 构建近表面原子层的振动态分布, 分析不同对称方向上表面模的局域特征和极化方式. 以极化矢量为考察对象, 直观、形象地展示了表面模色散支之间的避免交叉现象和独立性实交叉现象.

关键词:

表面声子谱 /
表面模 /
局域 /
极化

Abstract

Based on the theory of surface lattice dynamics, the surface phonon spectrums along three symmetrical directions of $\bar \varGamma \bar L$, $\bar L\bar M$ and $\bar \varGamma \bar M$ are simulated for the W(100) surface by using the modified analytic embedded atom method. The polarization vectors at different symmetrical points are also calculated. According to the criterion and marking method of surface mode, the surface modes along different symmetrical directions are drawn, the distribution range and mode coupling of surface modes are discussed as well. The vibration frequencies of surface modes calculated by us have been compared to available experimental datum and some theoretical values correspondingly. The results display that the present results are general agreement with the referenced experimental or theoretical results. Based on the calculated polarization vector, the surface vibration states are constructed for the atomic layers in the neighboring surface. And the polarization and local features of the surface modes along different symmetrical directions are analyzed. The results show that there are some coupling phenomena between surface mode dispersion, such as avoid crossing and independence crossing. The avoid crossing is found between the surface-mode branch S₁ and the surface-mode branch S₂ near ${\bar \zeta _y} = 0.32$ along $\bar L\bar M$ direction. In the region, going from $\bar L$ to $\bar M$, S₁ changes from y polarization to z polarization, and S₂ changes from z polarization to y polarization. The independence crossings exist between surface-mode branch S₁ and surface-mode branch S₂ at ${\bar \zeta _x} = 0.5$ along $\bar \varGamma \bar L$ direction, and surface-mode branch S₂ and surface-mode branch S₃ at ${\bar \zeta _x} = 0.5$ along $\bar L\bar M$ direction, respectively. Before and after the crossings, the polarization and local features of the surface modes have not changed. Inspection of the polarization vectors, the coupling phenomena are iconically demonstrated.

Keywords:

作者及机构信息

1.
西安工程大学理学院, 西安　710048

2.
西北工业大学理学院, 西安　710072

通信作者: 张晓军, xiaoj_zhang@126.com

基金项目: 国际级- 基于原子相干的非线性级联效应控制光孤子传输(61405151)

Authors and contacts

1.
School of Science, Xi’an Polytechnic University, Xi’an 710048, China

2.
School of Science, Northwestern Polytechnical University, Xi’an 710072, China

Corresponding author: Zhang Xiao-Jun, xiaoj_zhang@126.com

文章全文 : translate this paragraph

参考文献

[1]	Bagci S, Duman S, Mutuncu H M, Srivastava G P 2009 J. Phys. Chem. Solids 70 444 Google Scholar
[2]	Barrett C, Wang L W 2016 Comp. Phys. Commun. 200 27 Google Scholar
[3]	Campi D, Bmasconi M, Benedek G, Graham A P, Toennies J P 2017 Phys. Chem. Chem. Phys. 19 16358 Google Scholar
[4]	Hayes W W, Amjad A T, Anemone G, Manson J R 2018 Surf. Sci. 678 20 Google Scholar
[5]	Taleb A A, Anemone G, Farias D, Miranda R 2016 Carbon 99 416 Google Scholar
[6]	Anton T, Patrick K, Michael M R, Davide C, Marco B 2013 Phys. Rev. B 87 035410 Google Scholar
[7]	Minamitani E, Takagi N, Arafune R, Thomas F, Komeda T 2018 Prog. Surf. Sci. 93 131 Google Scholar
[8]	Matsushita S Y, Hu C, Kawamoto E, Kato H, Watanabe K, Suto S 2015 J. Chem. Phys. 143 214702 Google Scholar
[9]	Hu G, Huang J Q, Wang Y N, Yang T, Dong B J, Wang J Z, Zhao B, Ali S, Zhang Z D 2018 Chin. Phys. B 27 086301 Google Scholar
[10]	Chen Y, Tong S Y, Kim J S, Kesmodel L L, Rodach T, Bohnen K P, Ho K M 1991 Phys. Rev. B 44 11394 Google Scholar
[11]	Benedek G, Ellis J, Luo N S, Reichmuth A, Ruggerone P, Toennies J P 1993 Phys. Rev. B 48 4917 Google Scholar
[12]	杨剑瑜, 邓辉球, 胡望宇 2004 53 1946 Google Scholar Yang J Y, Deng H Q, Hu W Y 2004 Acta Phys. Sin. 53 1946 Google Scholar
[13]	Yndurain F, Jigato M P 2008 Phys. Rev. Let. 100 205501 Google Scholar
[14]	Łażewski J, Korecki J, Parlinski K 2007 Phys. Rev. B 75 054303
[15]	Benedek G, Bernasconi M, Chis V, Chulkov E, Echenique P M, Hellsing B, Toennies J P 2010 J. Phys.: Condens. Matter 22 084020 Google Scholar
[16]	Rusina G G, Borisova S D, Chulkov EV 2016 J. Exp. Theor. Phys. 122 283
[17]	Allen R E, Allredge G P, Wette F W 1971 Phys. Rev. B 4 1648 Google Scholar
[18]	Allen R E, Allredge G P, Wette F W 1971 Phys. Rev. B 4 1661 Google Scholar
[19]	Ouyang Y F, Zhang B W, Liao S Z, Jin Z P 1996 Z Phys. B 101 161 Google Scholar
[20]	Zhang B W, Ouyang Y F, Liao S Z, Jin Z P 1999 Phys. B 262 218 Google Scholar
[21]	Hu W Y, Shu X L, Zhang B W 2002 Comp. Mater. Sci. 23 175 Google Scholar
[22]	Luo W H, Hu W Y, Su K L, Liu F S 2013 Appl. Surf. Sci. 265 375 Google Scholar
[23]	Jin H S, Pak J Y, Jong Y S 2017 Appl. Phys. A 123 257
[24]	Zhang X J, Chen C L, Feng F L 2013 Chin. Phys. B 22 096301 Google Scholar
[25]	Fasolino A, Tosatti E 1987 Phys. Rev. B 35 4264 Google Scholar
[26]	Zhang X J, Chen C L 2016 Chin. Phys. B 25 016301 Google Scholar
[27]	Nelson J S, Sowa E C, Murray S D 1988 Phys. Rev. Let. 61 1977 Google Scholar
[28]	Ernst H J, Hulpke E, Toennies J P 1992 Phys. Rev. B 46 16081 Google Scholar
[29]	Joubert D P 1988 J. Phys. C: Solid State Phys. 21 4233 Google Scholar
[30]	Sklyadneva I Y, Rusina G G, Chulkov E V 1998 Surf. Sci. 416 17 Google Scholar
[31]	Heid R, Bohnen K P 2003 Phys. Rep. 387 151 Google Scholar

施引文献

图 1 W(100)表面结构　(a)正格点阵; (b)倒格点阵

Fig. 1. Surface structure of W (100): (a) Crystal lattice; (b) reciprocal lattice.

下载: 全尺寸图片幻灯片

图 2 W(100)表面声子谱

Fig. 2. Surface phonon spectrum of W(100)

下载: 全尺寸图片幻灯片

图 3 W(100)表面模分布

Fig. 3. Surface mode distribution of W(100).

下载: 全尺寸图片幻灯片

图 4 S₁表面模的计算结果和实验值的比较

Fig. 4. Comparison of calculated S₁ surface mode and experimental value.

下载: 全尺寸图片幻灯片

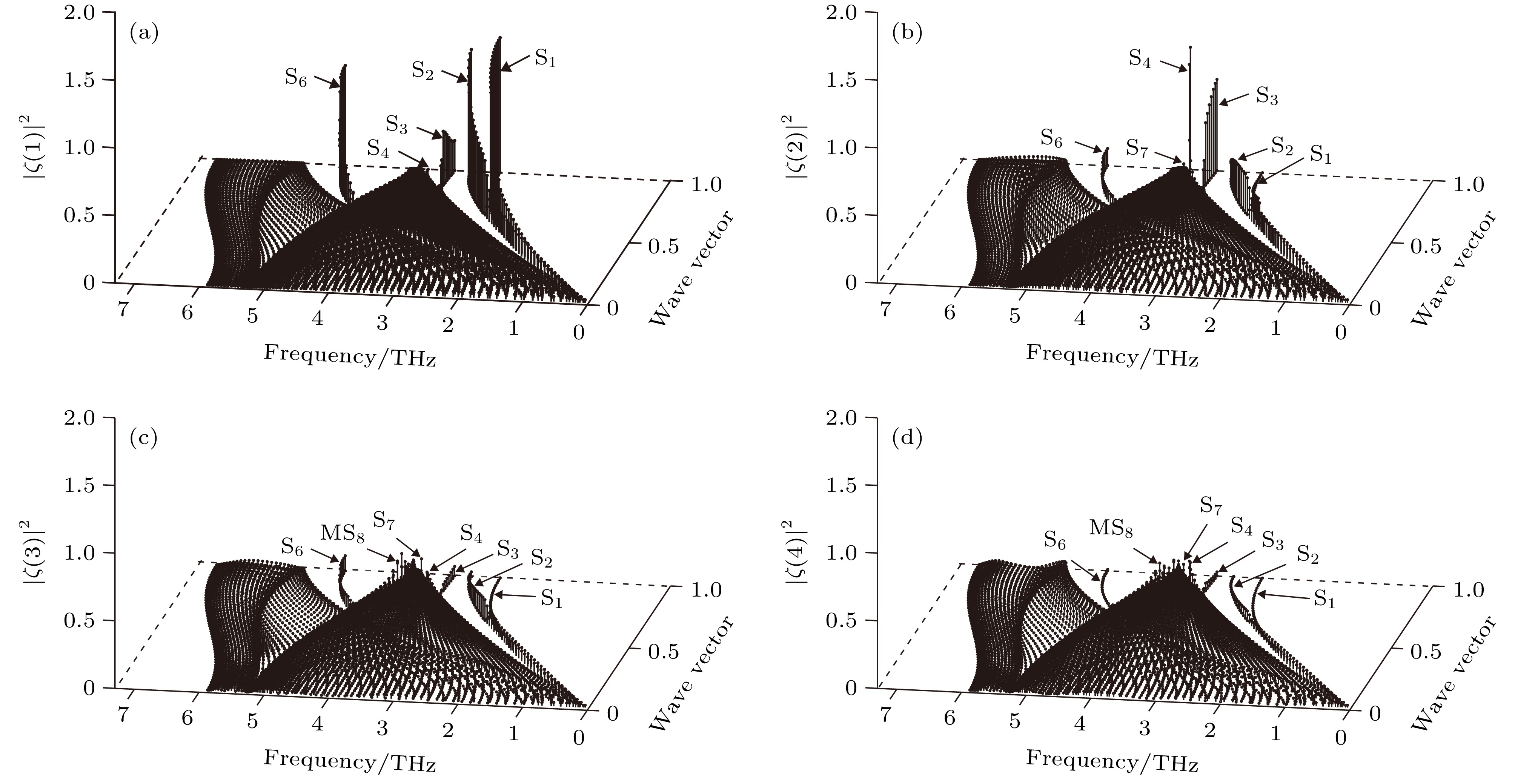
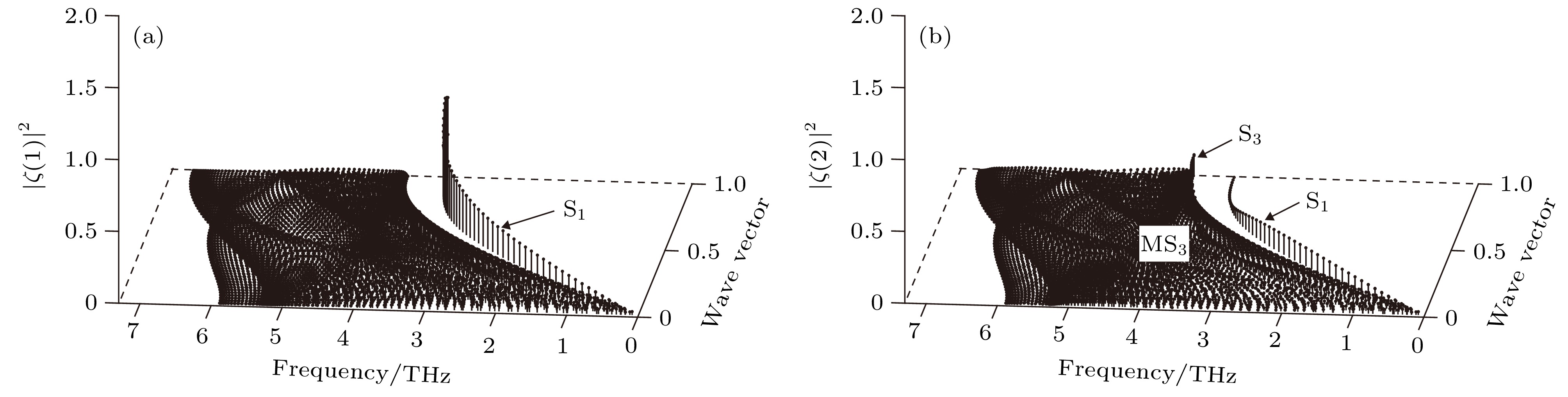
图 5 W(100)近表面原子层沿$\bar \varGamma \bar L$对称方向的局域振动态密度　(a)第1原子层; (b)第2原子层; (c)第3原子层; (d)第4原子层

Fig. 5. Local vibrational state density of atomic layers in the vicinity of the W (100) surface along $\bar \varGamma \bar L$ symmetry direction: (a) First atomic layer; (b) second atomic layer; (c) third atomic layer; (d) fourth atomic layer.

下载: 全尺寸图片幻灯片

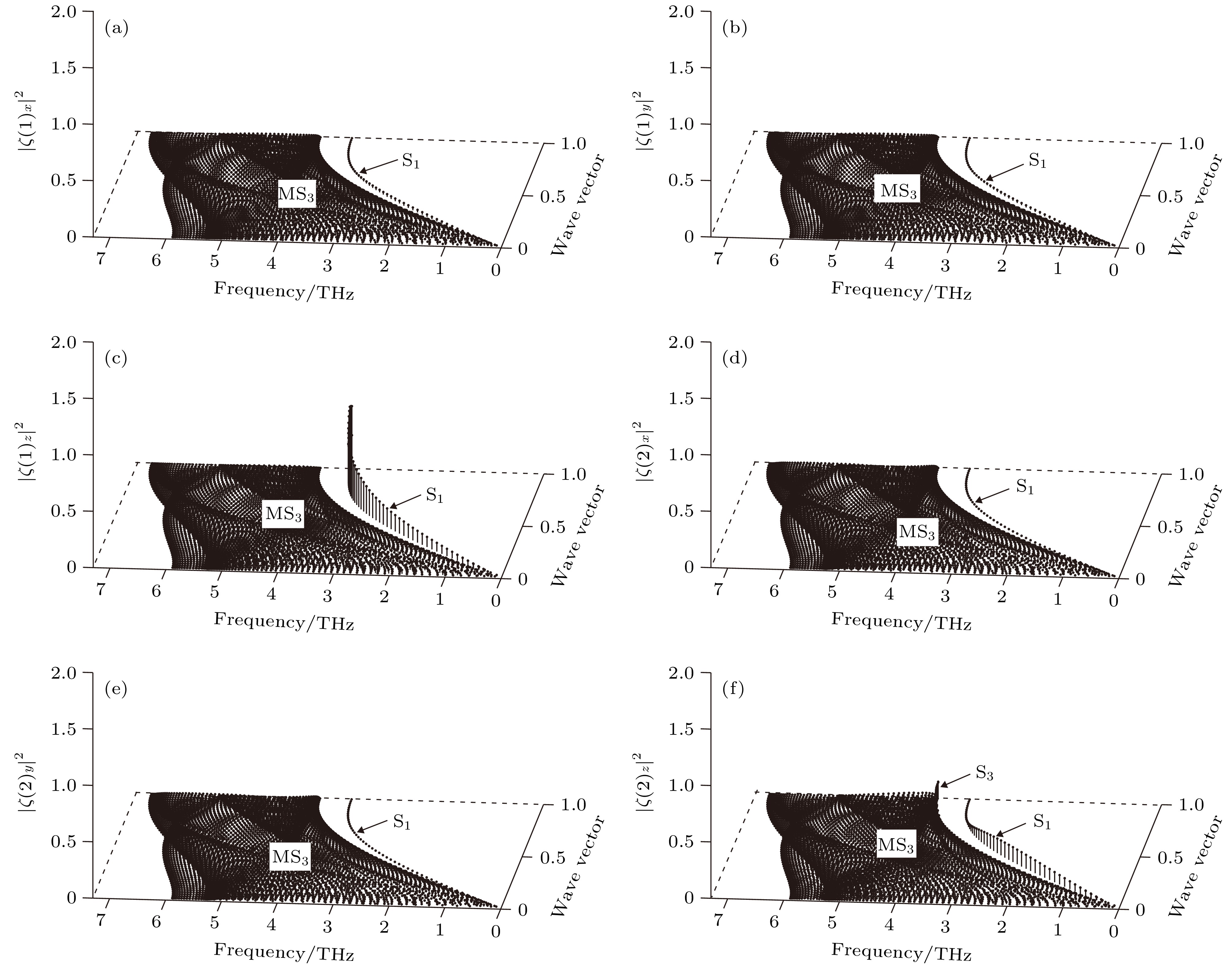
图 6 W(100)近表面原子层沿$\bar \varGamma \bar L$对称方向的极化态密度　(a)第1原子层沿x方向极化; (b)第1原子层沿y方向极化; (c)第1原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化

Fig. 6. Polarizing state density of atomic layers in the vicinity of the W (100) surface along $\bar \varGamma \bar L$ symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

下载: 全尺寸图片幻灯片

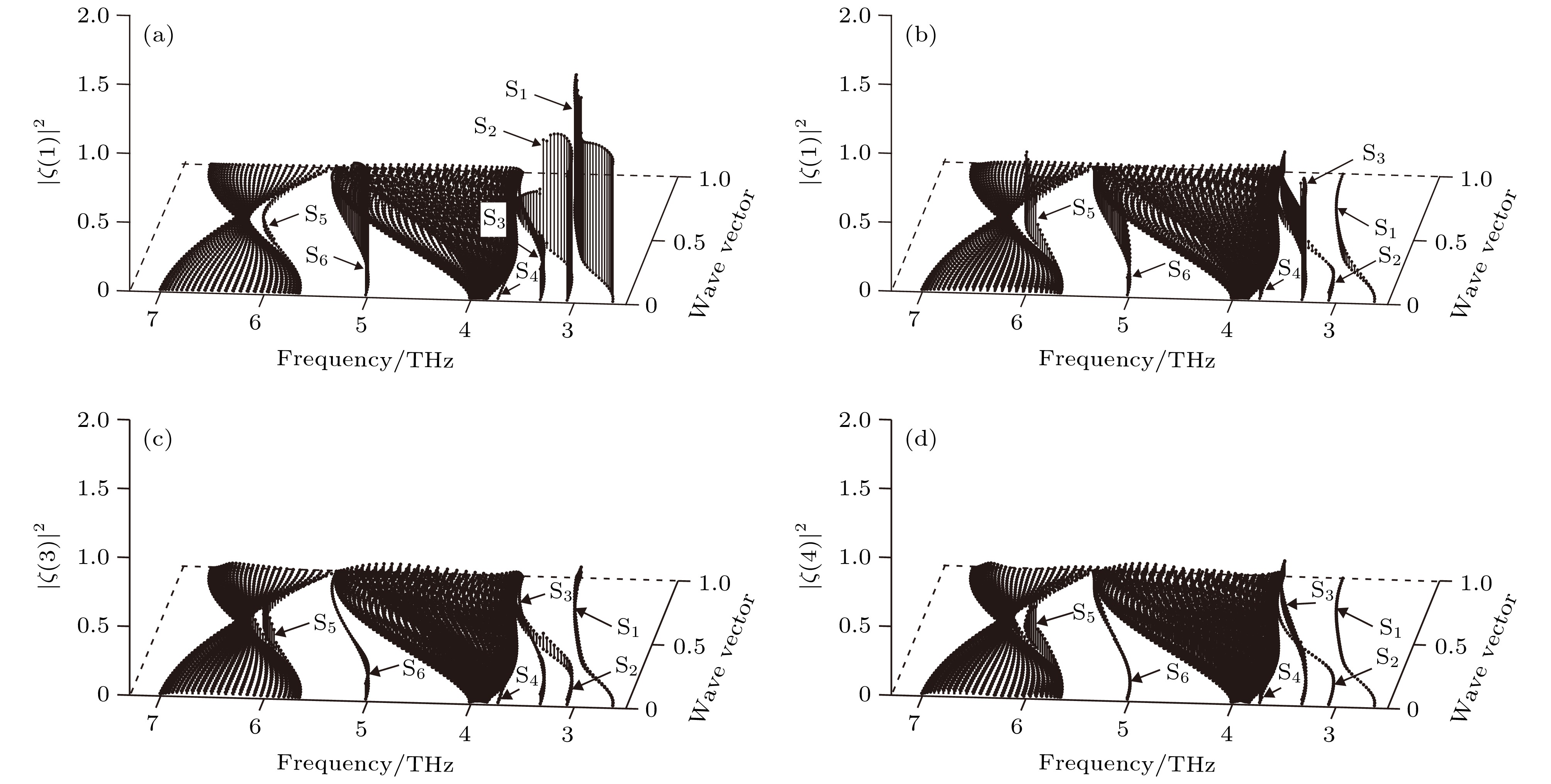
图 7 W(100)近表面原子层沿$\bar L\bar M$方向上的局域振动态密度　(a)第1原子层; (b)第2原子层; (c)第3原子层; (d)第4原子层

Fig. 7. Local vibrational state density of atomic layers in the vicinity of the W (100) surface along $\bar L\bar M$ symmetry direction: (a) First atomic layer; (b) second atomic layer; (c) third atomic layer; (d) fourth atomic layer.

下载: 全尺寸图片幻灯片

图 8 W(100)近表面原子层沿$\bar L\bar M$方向的极化态密度　(a)第1原子层沿x方向极化; (b)第1原子层沿y方向极化; (c)第1原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化

Fig. 8. Polarizing state density of atomic layers in the vicinity of the W (100) surface along $\bar L\bar M$ symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

下载: 全尺寸图片幻灯片

图 9 W(100)近表面原子层沿$\bar \Gamma \bar M$方向上的局域振动态密度　(a)第1原子层; (b)第2原子层

Fig. 9. Local vibration state density of atomic layers in the vicinity of the W (100) surface along $ \bar \Gamma \bar M $ symmetry direction: (a) First atomic layer; (b) second atomic layer.

下载: 全尺寸图片幻灯片

图 10 W(100)近表面原子层沿$\bar \varGamma \bar M$方向的极化态密度　(a)第1原子层沿x方向极化; (b)第1原子层沿y方向极化; (c)第1原子层沿z方向极化; (d)第2原子层沿x方向极化; (e)第2原子层沿y方向极化; (f)第2原子层沿z方向极化

Fig. 10. Polarizing state density of atomic layers in the vicinity of the W (100) surface along $\bar \varGamma \bar M$ symmetry direction: (a) x polarization for first atomic layer; (b) y polarization for first atomic layer; (c) z polarization for first atomic layer; (d) x polarization for second atomic layer; (e) y polarization for second atomic layer; (f) z polarization for second atomic layer.

下载: 全尺寸图片幻灯片

表 1 高对称点处W(100)表面模振动频率的比较 (单位: THz)

Table 1. Comparison of vibration frequencies of surface modes for W(100) at high symmetry points (in units of THz).

Method $\bar L$ $\bar M$
S₁ S₂ S₃ S₆ S₁ S₃

MAEAM 2.63 3.08 3.33 5.03 3.44 3.91
EHA 2.77 2.98 3.46 5.31 3.27 3.99
TBM 3.21 3.34 3.81 5.06 3.46 3.93

下载: 导出CSV

map

[1]	Bagci S, Duman S, Mutuncu H M, Srivastava G P 2009 J. Phys. Chem. Solids 70 444 Google Scholar
[2]	Barrett C, Wang L W 2016 Comp. Phys. Commun. 200 27 Google Scholar
[3]	Campi D, Bmasconi M, Benedek G, Graham A P, Toennies J P 2017 Phys. Chem. Chem. Phys. 19 16358 Google Scholar
[4]	Hayes W W, Amjad A T, Anemone G, Manson J R 2018 Surf. Sci. 678 20 Google Scholar
[5]	Taleb A A, Anemone G, Farias D, Miranda R 2016 Carbon 99 416 Google Scholar
[6]	Anton T, Patrick K, Michael M R, Davide C, Marco B 2013 Phys. Rev. B 87 035410 Google Scholar
[7]	Minamitani E, Takagi N, Arafune R, Thomas F, Komeda T 2018 Prog. Surf. Sci. 93 131 Google Scholar
[8]	Matsushita S Y, Hu C, Kawamoto E, Kato H, Watanabe K, Suto S 2015 J. Chem. Phys. 143 214702 Google Scholar
[9]	Hu G, Huang J Q, Wang Y N, Yang T, Dong B J, Wang J Z, Zhao B, Ali S, Zhang Z D 2018 Chin. Phys. B 27 086301 Google Scholar
[10]	Chen Y, Tong S Y, Kim J S, Kesmodel L L, Rodach T, Bohnen K P, Ho K M 1991 Phys. Rev. B 44 11394 Google Scholar
[11]	Benedek G, Ellis J, Luo N S, Reichmuth A, Ruggerone P, Toennies J P 1993 Phys. Rev. B 48 4917 Google Scholar
[12]	杨剑瑜, 邓辉球, 胡望宇 2004 53 1946 Google Scholar Yang J Y, Deng H Q, Hu W Y 2004 Acta Phys. Sin. 53 1946 Google Scholar
[13]	Yndurain F, Jigato M P 2008 Phys. Rev. Let. 100 205501 Google Scholar
[14]	Łażewski J, Korecki J, Parlinski K 2007 Phys. Rev. B 75 054303
[15]	Benedek G, Bernasconi M, Chis V, Chulkov E, Echenique P M, Hellsing B, Toennies J P 2010 J. Phys.: Condens. Matter 22 084020 Google Scholar
[16]	Rusina G G, Borisova S D, Chulkov EV 2016 J. Exp. Theor. Phys. 122 283
[17]	Allen R E, Allredge G P, Wette F W 1971 Phys. Rev. B 4 1648 Google Scholar
[18]	Allen R E, Allredge G P, Wette F W 1971 Phys. Rev. B 4 1661 Google Scholar
[19]	Ouyang Y F, Zhang B W, Liao S Z, Jin Z P 1996 Z Phys. B 101 161 Google Scholar
[20]	Zhang B W, Ouyang Y F, Liao S Z, Jin Z P 1999 Phys. B 262 218 Google Scholar
[21]	Hu W Y, Shu X L, Zhang B W 2002 Comp. Mater. Sci. 23 175 Google Scholar
[22]	Luo W H, Hu W Y, Su K L, Liu F S 2013 Appl. Surf. Sci. 265 375 Google Scholar
[23]	Jin H S, Pak J Y, Jong Y S 2017 Appl. Phys. A 123 257
[24]	Zhang X J, Chen C L, Feng F L 2013 Chin. Phys. B 22 096301 Google Scholar
[25]	Fasolino A, Tosatti E 1987 Phys. Rev. B 35 4264 Google Scholar
[26]	Zhang X J, Chen C L 2016 Chin. Phys. B 25 016301 Google Scholar
[27]	Nelson J S, Sowa E C, Murray S D 1988 Phys. Rev. Let. 61 1977 Google Scholar
[28]	Ernst H J, Hulpke E, Toennies J P 1992 Phys. Rev. B 46 16081 Google Scholar
[29]	Joubert D P 1988 J. Phys. C: Solid State Phys. 21 4233 Google Scholar
[30]	Sklyadneva I Y, Rusina G G, Chulkov E V 1998 Surf. Sci. 416 17 Google Scholar
[31]	Heid R, Bohnen K P 2003 Phys. Rep. 387 151 Google Scholar

[1]	韦宜政, 孙超, 朱启轩. 浅海矢量声场极化特性的深度分布规律(已撤稿). , 2024, 73(9): 094302. doi: 10.7498/aps.73.20231767
[2]	陈昊鹏, 聂永杰, 李国倡, 魏艳慧, 胡昊, 鲁广昊, 李盛涛, 朱远惟. 聚合物分散液晶薄膜的极化特性及其对电光性能的影响. , 2023, 72(17): 177701. doi: 10.7498/aps.72.20230664
[3]	张东, 娄文凯, 常凯. 半导体极性界面电子结构的理论研究. , 2019, 68(16): 167101. doi: 10.7498/aps.68.20191239
[4]	秦黎, 李泽亚, 许静平, 张利伟, 羊亚平. 磁单负材料板附近的原子的自发辐射场分布. , 2015, 64(1): 014206. doi: 10.7498/aps.64.014206
[5]	孙凯, 何志群, 梁春军. 多温度阶梯退火对有机聚合物太阳能电池器件性能的影响. , 2014, 63(4): 048801. doi: 10.7498/aps.63.048801
[6]	屈少华, 曹万强. 球形无规键无规场模型研究弛豫铁电体极化效应. , 2014, 63(4): 047701. doi: 10.7498/aps.63.047701
[7]	黄旭东, 冯玉军, 唐帅. 掺镧锆锡钛酸铅陶瓷极化强度变化量对电子发射电流强度的影响. , 2012, 61(8): 087702. doi: 10.7498/aps.61.087702
[8]	陈龙天, 程用志, 聂彦, 龚荣洲. 人工异向介质调控电磁波极化特性的实验与仿真研究. , 2012, 61(9): 094203. doi: 10.7498/aps.61.094203
[9]	赵静波, 杜红亮, 屈绍波, 张红梅, 徐卓. A位等价与非等价取代对(K0.5Na0.5)NbO3陶瓷极化的影响. , 2011, 60(10): 107701. doi: 10.7498/aps.60.107701
[10]	尚英, 霍丙忠, 孟春宁, 袁景和. 并矢格林函数下的球形超透镜. , 2010, 59(11): 8178-8183. doi: 10.7498/aps.59.8178
[11]	孙贤明, 哈恒旭. 基于反射太阳光反演气溶胶光学厚度和有效半径. , 2008, 57(9): 5565-5570. doi: 10.7498/aps.57.5565
[12]	杨凤霞, 张端明, 邓宗伟, 姜胜林, 徐洁, 李舒丹. 基体电导率对0-3型铁电复合材料高压极化行为及损耗的影响. , 2008, 57(6): 3840-3845. doi: 10.7498/aps.57.3840
[13]	顾晓玲, 郭霞, 吴迪, 李一博, 沈光地. 表面InGaN厚度对GaN基发光二极管特性的影响. , 2008, 57(2): 1220-1223. doi: 10.7498/aps.57.1220
[14]	顾晓玲, 郭霞, 吴迪, 徐丽华, 梁庭, 郭晶, 沈光地. GaN基多量子阱发光二极管的极化效应和载流子不均匀分布及其影响. , 2007, 56(8): 4977-4982. doi: 10.7498/aps.56.4977
[15]	朱振业, 王彪, 郑跃, 王海, 李青坤, 李晨亮. 应力作用下铁电超晶格BaTiO3/SrTiO3的结构和极化的第一性原理研究. , 2007, 56(10): 5986-5989. doi: 10.7498/aps.56.5986
[16]	刘洪, 蒲朝辉, 龚小刚, 王志红, 黄惠东, 李言荣, 肖定全, 朱建国. (111)取向(Pb,La)TiO3铁电薄膜中90°纳米带状畴与热释电性能的研究. , 2006, 55(11): 6123-6128. doi: 10.7498/aps.55.6123
[17]	徐任信, 陈文, 周静. 聚合物电导率对0-3型压电复合材料极化性能的影响. , 2006, 55(8): 4292-4297. doi: 10.7498/aps.55.4292
[18]	张春福, 郝跃, 游海龙, 张金凤, 周小伟. 界面电偶极子对GaN/AlGaN/GaN光电探测器紫外/太阳光选择比的影响. , 2005, 54(8): 3810-3814. doi: 10.7498/aps.54.3810
[19]	郭冠军, 苏林, 毕思文. 风成海面的极化辐射. , 2005, 54(5): 2448-2452. doi: 10.7498/aps.54.2448
[20]	杨剑瑜, 邓辉球, 胡望宇. Ag（110）表面声子谱的分析型EAM模型计算. , 2004, 53(6): 1946-1951. doi: 10.7498/aps.53.1946

计量

文章访问数: 6110
PDF下载量: 80
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

改进分析型嵌入原子法在W(100)表面声子谱中的应用