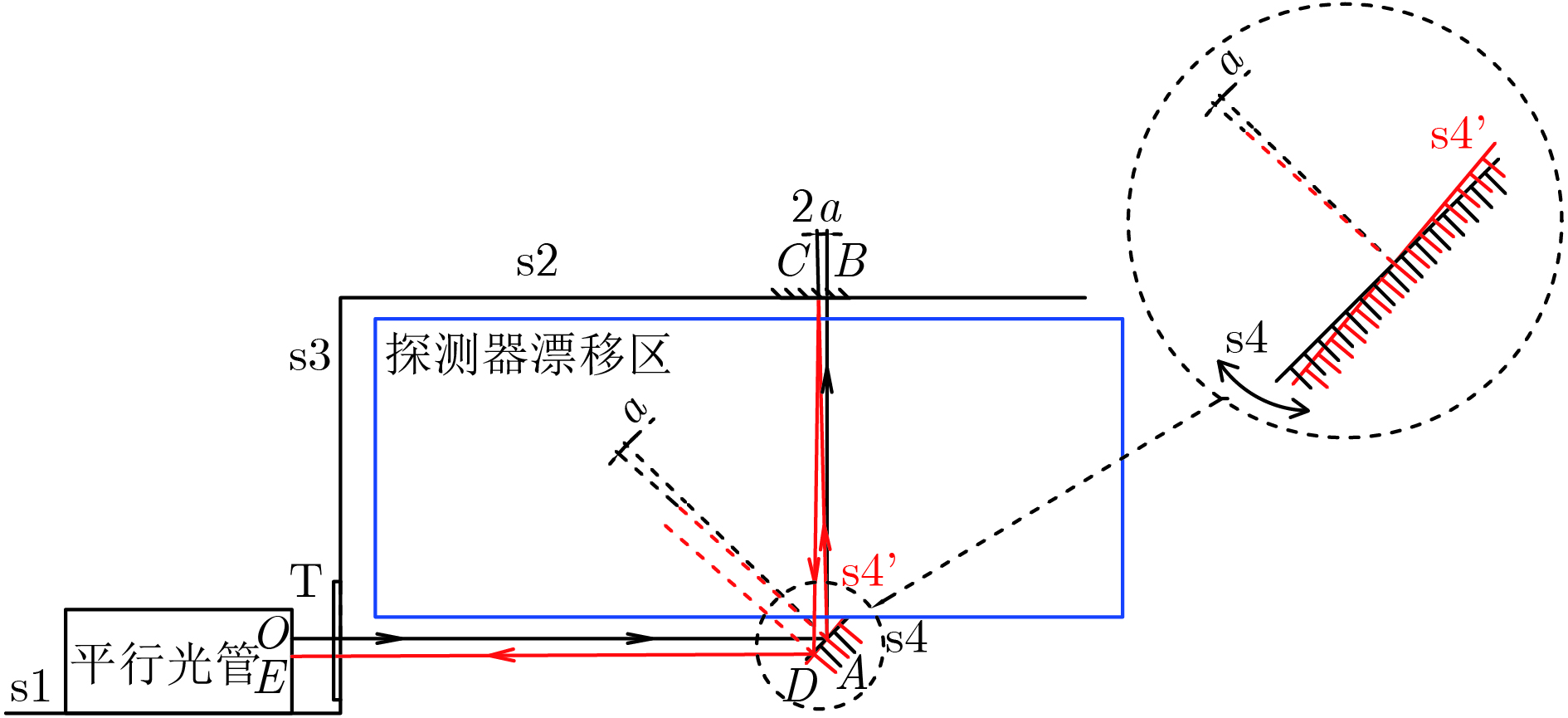
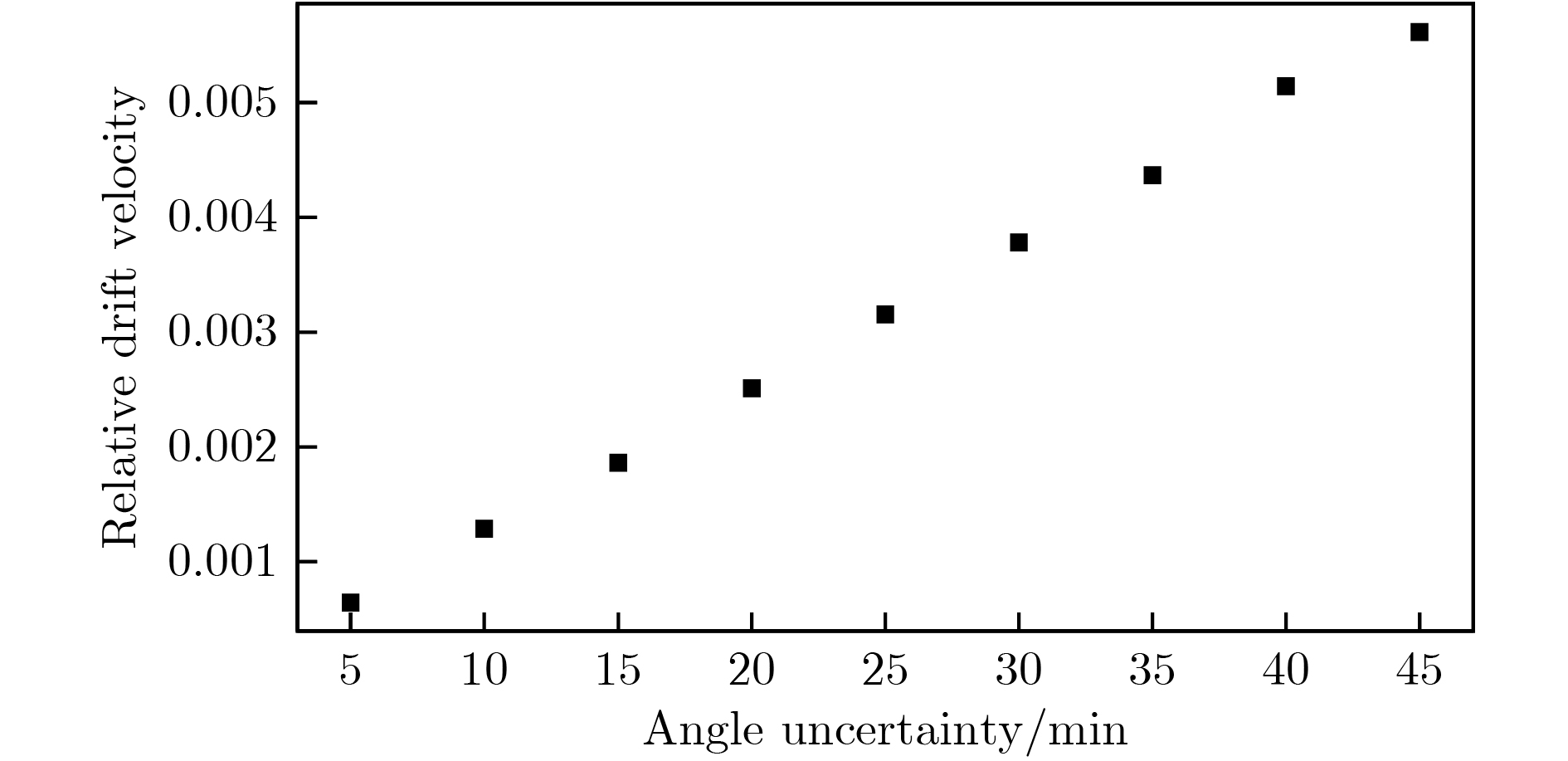
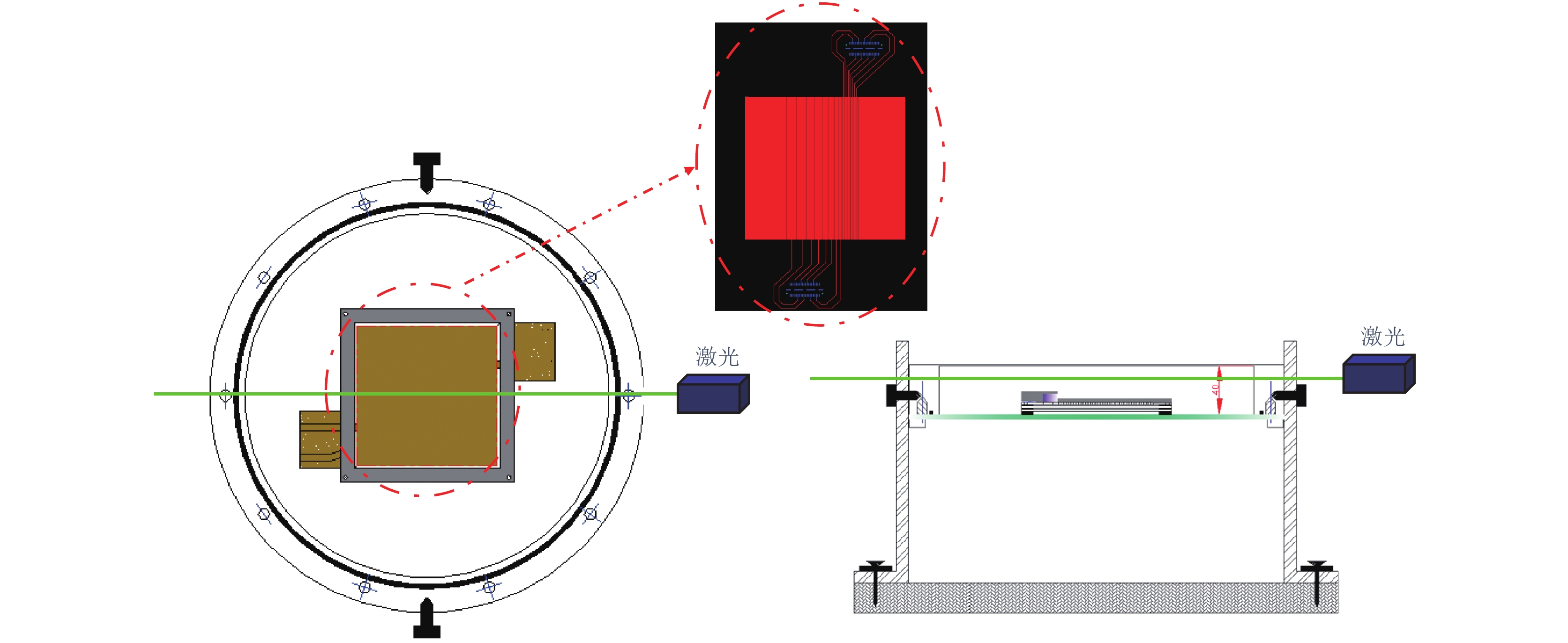
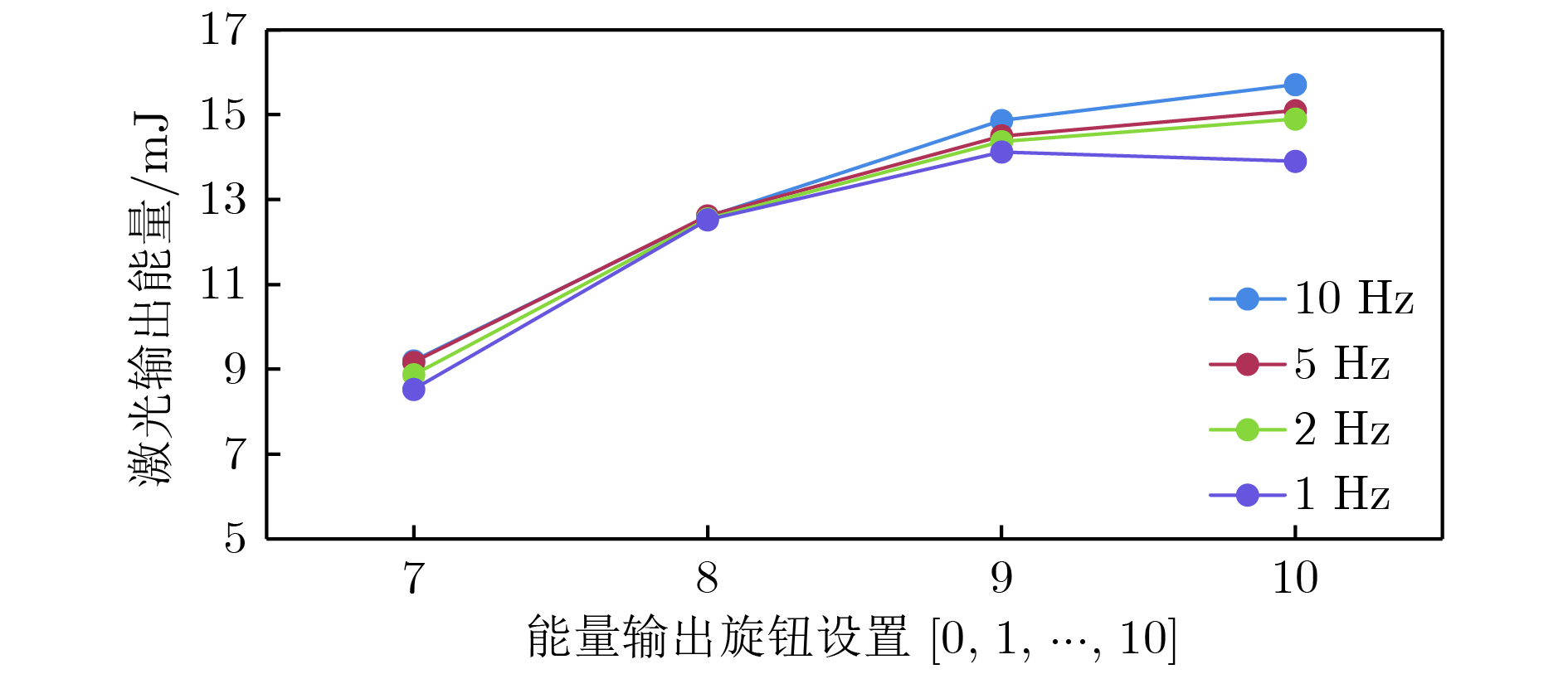
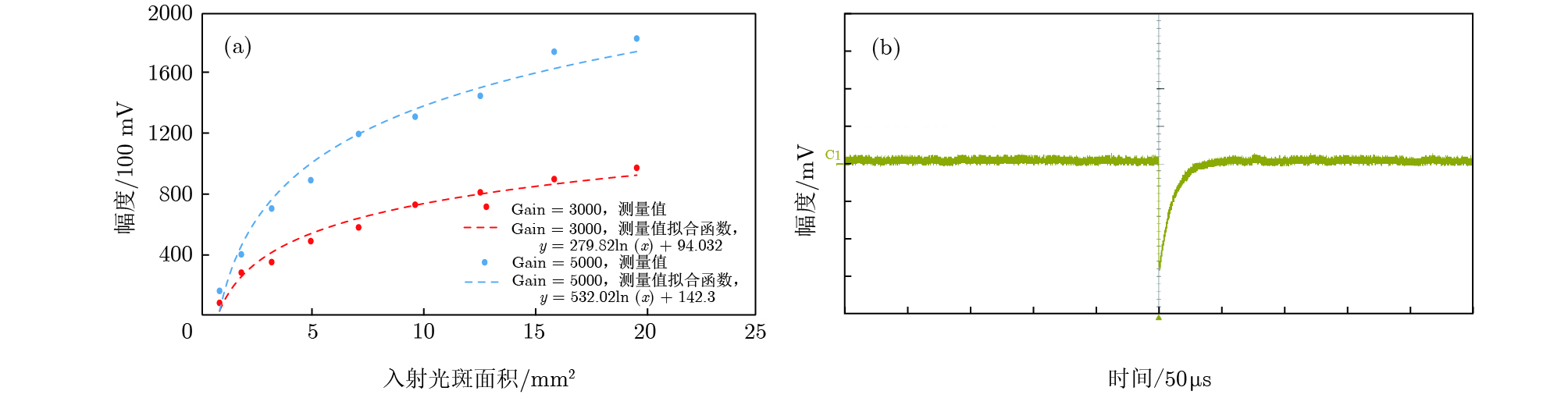
-
在气体探测器研究中, 利用266 nm紫外激光的双光子电离物理机制使气体电离产生可测量的信号, 是一种重要的标定方法. 随着微结构气体探测器(MPGD)的不断发展, 用紫外激光标定来实现较高精度位置分辨率成为了一种研究需求, 对此有两个关键技术问题需要解决: 实验研究激光可测信号大小以及激光指向精度. 分析和模拟计算了紫外光电离信号大小和激光调光误差, 基于微结构气体电子倍增器探测器与266 nm波长激光束, 在工作气体Ar/CO2(70/30)中, 测量了不同光斑面积与输出信号的关系; 设计和研制了紫外激光调光系统, 实验测量了紫外光调光偏差. 模拟结果与实验结果对比分析表明: 紫外激光束作用于气体探测器, 探测器增益在5000, 前放增益为10 mV/fC时, 6 mm读出条宽输出信号幅度约400 mV; 在探测器内传播距离为400 mm时, 较短时间内(10—20 min)实验调光指向精度可以保证小于5′, 引入z向偏差最大可以达到0.33 mm, 对应z向漂移速度的测量相对误差为6.4 × 10 −4. 该研究为MPGD与紫外激光标定实验设计提供主要的设计参考.In the study of the gas detectors, it is an important calibration method to use the ultraviolet (UV) laser with two-photon ionization mechanism for producing ionized signal. In the last decades, micro pattern gas detector, especially gaseous electron multiplier and micromesh gaseous detector, has been widely used in high energy experiments. These kinds of gaseous detectors have the advantages of higher ion backflow suppression ability, smaller E × B effect and good radiation resistance under the relatively higher count rate environment. To obtain a higher spatial resolution with a UV laser calibration system in gaseous electron multiplier detector, two critical technical issues remain to be resolved: the measurability of the laser signal and the accuracy of the laser beam position. In this paper, the studies in simulation and experiment are conducted to discuss these two critical questions. In the simulation section, the simulation results provide an estimation of signal in the gaseous electron multiplier detector with UV laser of 266 nm wavelength in the mixture working gases of Ar/CO2 (70/30), and give an evaluation of the laser pointing accuracy and the possible relative error of the electron drift velocity. In the experiment section, a UV laser calibration prototype is designed and developed. A pulsed laser of 266 nm wavelength is used as a signal source, which has a Gaussian-like cross section with a frequency of 10 Hz. The experimental results indicate that the signal of the UV laser in a triple gaseous electron multiplier detector reaches 400 mV for a readout strip width of 6 mm, a gain of detector of 5000, and a gain of amplifier of 10 mV/fC. For the calibration laser, the angle accuracy is discussed and tested. The angle uncertainty of the laser can be kept under 5′, and the accuracy of the drift velocity can reach 6.4 × 10−4 with a shift of 0.33 mm in the z direction when the laser beam transmits a distance of 400 mm in the gas chamber. All of these results show that the laser beam specific parameters are the main reference for designing the prototype detector. According to the optimal parameters, a gaseous prototype detector will be tested in the next study.
[1] Leonard A 2015 Ph. D. Dissertation (Bruxelles: Université Libre de Bruxelles)
[2] Delbart A, de Oliveira R, Derre J, Giomataris Y, Jeanneau F, Papadopoulos Y, Rebourgeard Ph 2001 Nucl. Instrum. Methods A 461 84
Google Scholar
[3] Zibell A 2014 J. Instrum. 9 C08013
Google Scholar
[4] Sauli F 2002 Nucl. Instrum. Methods A 477 1
Google Scholar
[5] Sauli F 1997 Nucl. Instrum. Methods A 386 531
Google Scholar
[6] Chernyshova M, Czarski T, Dominik W, Jakubowska K, Rzadkiewicz J, Scholz M, Pozniak K, Kasprowicz G, Zabolotny W 2014 J. Instrum. 9 C03003
Google Scholar
[7] Giomataris I, Oliveira R D, Andriamonje S, Aune S, Charpak G, Colas P, Fanourakis G, Ferrer E, Giganon A, Rebourgeard Ph, Salin P 2006 Nucl. Instrum. Methods A 560 405
Google Scholar
[8] Giomataris, Y 1998 Nucl. Instrum. Methods A 419 239
Google Scholar
[9] Colas P, Giomataris I, Lepeltier V 2004 Nucl. Instrum. Methods A 535 226
Google Scholar
[10] The LHCb collaboration 2015 Int. J. Mod. Phys. A 30 1530022
Google Scholar
[11] Balla A, Bencivenni G, Branchini P, Ciambrone P, Czerwinski E, de Lucia E, Cicco A, Di Domenici D, Felici G, Morello G 2017 Nucl. Instrum. Methods A 845 266
Google Scholar
[12] Dørheim S 2012 J. Instrum. 7 C03011
[13] Adinoff B, Kramer G L, Petty F 2007 Nucl. Instrum. Methods A 577 455
Google Scholar
[14] Ketzer B, Weitzel Q, Paul S, Sauli F, Ropelewski L 2004 Nucl. Instrum. Methods A 535 314
Google Scholar
[15] Hilke H J 2010 Rep. Prog. Phys. 73 116201
Google Scholar
[16] Attie D 2009 Nucl. Instrum. Methods A 598 89
Google Scholar
[17] Kane S, May J, Miyamoto J, Shipsey I 2003 Nucl. Instrum. Methods A 505 215
Google Scholar
[18] Hilke H J 1986 Nucl. Instrum. Methods A 252 169
Google Scholar
[19] Renault G, Nielsen B S, Westergaard J, Gaardhoje J J 2005 Czech. J. Phys. 55 1671
Google Scholar
[20] Antończyk D, Baechler J, Bramm R, Campagnolo R, Christiansen P, Frankenfeld U, Gonzalez Gutierrez C, Ivanov M, Kowalski M, Musa L, Przybyla A 2006 Nucl. Instrum. Methods A 565 551
Google Scholar
[21] Wikipedia https://en.wikipedia.org/wiki/Gaussian_beam [2018-08-30]
[22] 祁金刚, 李春杰 2007 物理实验 27 34
Google Scholar
Qi J G, Li C J 2007 Physics Experimentation 27 34
Google Scholar
[23] 王小胡, 王守印, 周虎, 张余彬 2006 仪器仪表学报 27 980
Google Scholar
Wang X H, Wang S Y, Zhou H, Zhang Y B 2006 Chinese Journal of Scientific Instrument 27 980
Google Scholar
-
图 3 激光调光精度与漂移速度相对精度的关系
Fig. 3. Angle uncertainty of laser beam with relative accuracy of drift velocity.
图 4 激光性能测试探测器模块装置示意图
Fig. 4. Diagram of performance test detector module with laser system.
图 5 多道能量刻度曲线(a)和55Fe/激光源(266 nm)能谱图(b)
Fig. 5. Calibration curves of multiple channel energy (a) and energy spectra of 55Fe/laser (266 nm) sources (b).
图 6 激光性能测试实验系统实物图和示意图
Fig. 6. Experiment photo and diagram of performance test with laser device.
图 8 激光电离信号 (a)激光电离信号随光斑面积变化; (b)典型的激光电离信号
Fig. 8. Signal of laser: (a) Variation of laser signals with plot area; (b) typical signal of laser beam.
图 9 激光调光系统装置图与调光示意图 (a)调光系统; (b) 45°反射镜s4粗调时平行光管内图像; (c) 45°反射镜细调后平行光管内反射图像
Fig. 9. Installation photos of laser dimming system and diagram of dimming: (a) Dimming system; (b) image in 45° collimator when s4 is adjusted rough; (c) image in 45° collimator when s4 is adjusted fine).
-
[1] Leonard A 2015 Ph. D. Dissertation (Bruxelles: Université Libre de Bruxelles)
[2] Delbart A, de Oliveira R, Derre J, Giomataris Y, Jeanneau F, Papadopoulos Y, Rebourgeard Ph 2001 Nucl. Instrum. Methods A 461 84
Google Scholar
[3] Zibell A 2014 J. Instrum. 9 C08013
Google Scholar
[4] Sauli F 2002 Nucl. Instrum. Methods A 477 1
Google Scholar
[5] Sauli F 1997 Nucl. Instrum. Methods A 386 531
Google Scholar
[6] Chernyshova M, Czarski T, Dominik W, Jakubowska K, Rzadkiewicz J, Scholz M, Pozniak K, Kasprowicz G, Zabolotny W 2014 J. Instrum. 9 C03003
Google Scholar
[7] Giomataris I, Oliveira R D, Andriamonje S, Aune S, Charpak G, Colas P, Fanourakis G, Ferrer E, Giganon A, Rebourgeard Ph, Salin P 2006 Nucl. Instrum. Methods A 560 405
Google Scholar
[8] Giomataris, Y 1998 Nucl. Instrum. Methods A 419 239
Google Scholar
[9] Colas P, Giomataris I, Lepeltier V 2004 Nucl. Instrum. Methods A 535 226
Google Scholar
[10] The LHCb collaboration 2015 Int. J. Mod. Phys. A 30 1530022
Google Scholar
[11] Balla A, Bencivenni G, Branchini P, Ciambrone P, Czerwinski E, de Lucia E, Cicco A, Di Domenici D, Felici G, Morello G 2017 Nucl. Instrum. Methods A 845 266
Google Scholar
[12] Dørheim S 2012 J. Instrum. 7 C03011
[13] Adinoff B, Kramer G L, Petty F 2007 Nucl. Instrum. Methods A 577 455
Google Scholar
[14] Ketzer B, Weitzel Q, Paul S, Sauli F, Ropelewski L 2004 Nucl. Instrum. Methods A 535 314
Google Scholar
[15] Hilke H J 2010 Rep. Prog. Phys. 73 116201
Google Scholar
[16] Attie D 2009 Nucl. Instrum. Methods A 598 89
Google Scholar
[17] Kane S, May J, Miyamoto J, Shipsey I 2003 Nucl. Instrum. Methods A 505 215
Google Scholar
[18] Hilke H J 1986 Nucl. Instrum. Methods A 252 169
Google Scholar
[19] Renault G, Nielsen B S, Westergaard J, Gaardhoje J J 2005 Czech. J. Phys. 55 1671
Google Scholar
[20] Antończyk D, Baechler J, Bramm R, Campagnolo R, Christiansen P, Frankenfeld U, Gonzalez Gutierrez C, Ivanov M, Kowalski M, Musa L, Przybyla A 2006 Nucl. Instrum. Methods A 565 551
Google Scholar
[21] Wikipedia https://en.wikipedia.org/wiki/Gaussian_beam [2018-08-30]
[22] 祁金刚, 李春杰 2007 物理实验 27 34
Google Scholar
Qi J G, Li C J 2007 Physics Experimentation 27 34
Google Scholar
[23] 王小胡, 王守印, 周虎, 张余彬 2006 仪器仪表学报 27 980
Google Scholar
Wang X H, Wang S Y, Zhou H, Zhang Y B 2006 Chinese Journal of Scientific Instrument 27 980
Google Scholar
下载:
计量
- 文章访问数: 7789
- PDF下载量: 49
- 被引次数: 0
