掺杂B, Cr, Mo, Ti, W, Zr后金刚石中正电子湮灭寿命计算

赵永生; 阎峰云; 刘雪

doi:10.7498/aps.73.20231269

摘要

金属基金刚石复合材料被广泛应用和研究, 但金刚石表面预处理所导致的空位、掺杂等缺陷对金属基与金刚石界面性能有很大影响. 尽管透射电子显微镜和能谱分析等技术已用于缺陷检测, 但这些方法存在局限性. 通过计算金刚石中正电子湮灭寿命, 可以准确评估金刚石的界面缺陷. 本文利用第一性原理计算方法, 采用多种正电子湮灭算法和增强因子, 计算了金刚石理想晶体、单空位、掺杂B, Cr, Mo, Ti, W和Zr后的正电子湮灭寿命. 结果显示, 在采用局域密度泛函时, 结合Boronski & Nieminen算法以及随机相位近似限制作为湮灭增强因子时, 计算得到的正电子湮灭寿命与文献的实验结果更吻合. 同时, 金刚石中B和Cr的掺杂使正电子湮灭寿命从由单空位119.87 ps增加为148.57 ps和156.82 ps. 总体来说, 金刚石中的空位和掺杂原子缺陷都会引起正电子湮灭寿命的变化. 这些发现为理解和优化金刚石界面提供了有价值的理论依据.

关键词:

金刚石 /
掺杂 /
正电子 /
湮灭寿命

Abstract

Metal-matrix diamond composites have been extensively used and studied, but vacancies, doping, and other defects caused by the pretreatment of the diamond surface significantly affect the interface property between the metal base and diamond. Although techniques like transmission electron microscopy and spectroscopy analysis have been used to detect defects, they present certain limitations. Calculating the positron annihilation lifetime in diamond provides an accurate assessment of interface defect in the diamond. This study uses first-principles calculation methods and adopts various positron annihilation algorithms and enhancement factors, to compute the positron annihilation lifetimes in ideal diamond crystals, single vacancies, and diamond crystals doped with B, Cr, Mo, Ti, W, and Zr. The results, obtained by using local density functional in combination with Boronski & Nieminen algorithms and random-phase approximation restriction as annihilation enhancement factors, indicate that the computed positron annihilation lifetime of diamond is 119.87 ps, which is consistent closely with the experimental result in the literature. Furthermore, after B, Cr, Mo, Ti, W, and Zr atoms are doped into diamond (doping atomic concentration of 1.6%), the positron annihilation lifetimes change from a single vacancy 119.87 ps to 148.57, 156.82, 119.05, 116.5, 117.62, and 115.74 ps respectively. This implies that the defects due to doped atoms in diamond change their positron annihilation lifetimes, with the influence varying according to the different atoms doped. Based on the calculated electron density in diamond vacancies and doped atom areas, it is discovered that doping atoms do not cause severe distortion in the diamond lattice. However, after B and Cr atoms are doped, the positron annihilation lifetime increases significantly. The primary reason is that the relatively low positron affinity of B and Cr atoms results in an extended positron residence time in the vacancy, thereby increasing the annihilation lifetime. Overall, vacancies and doped atom defects in diamond will cause its positron annihilation lifetime to change. The above conclusions provide crucial theoretical references for detecting and identifying interface defects caused by doping treatment on the diamond surface during the preparation of metal-matrix diamond composites.

Keywords:

作者及机构信息

1.
兰州理工大学, 省部共建有色金属先进加工与再利用国家重点实验室, 兰州　730060

2.
兰州工业学院机电工程学院, 兰州　730060

3.
兰州理工大学石油化工学院, 兰州　730060

通信作者: 阎峰云, yanfy@lut.edu.cn

基金项目: 甘肃省教育厅产业支撑计划(批准号: 2021CYZC-34)和甘肃省高等学校创新基金(批准号: 2021B-310)资助的课题.

Authors and contacts

1.
State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals, Lanzhou University of Technology, Lanzhou 730060, China

2.
School of Mechanical and Electrical Engineering, Lanzhou Institute of Technology, Lanzhou 730060, China

3.
School of Petrochemical Engineering, Lanzhou University of Technology, Lanzhou 730060, China

Corresponding author: Yan Feng-Yun, yanfy@lut.edu.cn

Funds: Project supported by the Industry Support Program of Educaiton Bureau of Gansu Province, China (Grant No. 2021CYZC-34) and the Higher Education Innovation Fund of Gansu Province, China (Grant No. 2021B-310).

文章全文 : translate this paragraph

参考文献

[1]	Stachel T, Luth R W 2015 Lithos 220 – 223 200
[2]	Bulanova G P 1995 J. Geochem. Explor. 53 1 Google Scholar
[3]	Wei L, Kuo P K, Thomas R L, et al. 1993 Phys. Rev. Lett. 70 3764 Google Scholar
[4]	Chakraborty P, Xiong G, Cao L, et al. 2018 Carbon 139 85 Google Scholar
[5]	Ciupiński Ł, Kruszewski M J, Grzonka J, et al. 2017 Mater. Des. 120 170 Google Scholar
[6]	Kidalov S V, Shakhov F M 2009 Materials 2 2467 Google Scholar
[7]	May P W 2000 Philos. Trans. R. Soc. London, Ser. A 358 473 Google Scholar
[8]	Liao M 2021 Funct. Diamond 1 29 Google Scholar
[9]	Gomez H, Groves M N, Neupane M R 2021 Carbon Trends 3 100033 Google Scholar
[10]	Pan Y, He X, Ren S, et al. 2018 Vacuum 153 74 Google Scholar
[11]	Soltani H M, Tayebi M 2020 Int. J. Refract. Met. Hard Mater. 87 105172 Google Scholar
[12]	Pillari L K, Bakshi S R, Chaudhuri P, et al. 2020 Adv. Powder Technol. 31 3657 Google Scholar
[13]	Zhang X Y, Xu M, Cao S Z, et al. 2020 Diamond Relat. Mater. 104 107755 Google Scholar
[14]	Jia J, Bai S, Xiong D, et al. 2019 Ceram. Int. 45 10810 Google Scholar
[15]	Liu Z, Zheng S, Lu Z, et al. 2018 Carbon 127 548 Google Scholar
[16]	Wu M, Chang L, Zhang L, et al. 2017 Surf. Coat. Technol. 325 490 Google Scholar
[17]	Contreras Cuevas A, Bedolla Becerril E, Martínez M S, et al. 2018 Metal Matrix Composites (Cham: Springer International Publishing
[18]	Bai G, Li N, Wang X, et al. 2018 J. Alloys Compd. 735 1648 Google Scholar
[19]	Bai G, Wang L, Zhang Y, et al. 2019 Mater. Charact. 152 265 Google Scholar
[20]	Liu X, Sun F, Wang L, et al. 2020 Appl. Surf. Sci. 515 146046 Google Scholar
[21]	Kang Q, He X, Ren S, et al. 2013 J. Alloys Compd. 576 380 Google Scholar
[22]	Che Q L, Chen X K, Ji Y Q, et al. 2015 Mater. Sci. Semicond. Process. 30 104 Google Scholar
[23]	Li J, Zhang H, Wang L, et al. 2016 Composites Part A 91 189 Google Scholar
[24]	Abyzov A M, Kidalov S V, Shakhov F M 2012 Appl. Therm. Eng. 48 72
[25]	He J, Wang X, Zhang Y, et al. 2015 Composites Part B 68 22 Google Scholar
[26]	Wang L, Li J, Bai G, et al. 2019 J. Alloys Compd. 781 800 Google Scholar
[27]	Dannefaer S 2007 Phys. Status Solidi C 4 3605 Google Scholar
[28]	Avalos V, Dannefaer S 2003 Phys. B: Condens. Matter 340 – 342 76
[29]	Siegel R W 1980 Annu. Rev. Mater. Sci. 10 393 Google Scholar
[30]	Tuomisto F, Makkonen I 2013 Rev. Mod. Phys. 85 1583 Google Scholar
[31]	Pu A, Bretagnon T, Kerr D, et al. 2000 Diamond Relat. Mater. 9 1450 Google Scholar
[32]	Sachdeva A, Sudarshan K, Pujari P, et al. 2004 Diamond Relat. Mater. 13 1719 Google Scholar
[33]	Hu X J, Ye J S, Liu H J, et al. 2008 Thin Solid Films 516 1699 Google Scholar
[34]	Jones R 2009 Diamond Relat. Mater. 18 820 Google Scholar
[35]	Fujii S, Nishibayashi Y, Shikata S, et al. 1995 J. Appl. Phys. 78 1510 Google Scholar
[36]	Eseev M, Kuziv I, Kostin A, et al. 2022 Materials 16 203 Google Scholar
[37]	Gonze X, Amadon B, Antonius G, et al. 2020 Comput. Phys. Commun. 248 107042 Google Scholar
[38]	Romero A H, Allan D C, Amadon B, et al. 2020 J. Chem. Phys. 152 124102 Google Scholar
[39]	Gonze X, Jollet F, Abreu Araujo F, et al. 2016 Comput. Phys. Commun. 205 106 Google Scholar
[40]	Gonze X, Amadon B, Anglade P M, et al. 2009 Comput. Phys. Commun. 180 2582 Google Scholar
[41]	Torrent M, Jollet F, Bottin F, et al. 2008 Comput. Mater. Sci. 42 337 Google Scholar
[42]	Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33 Google Scholar
[43]	Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272 Google Scholar
[44]	Boroński E, Nieminen R M 1986 Phys. Rev. B 34 3820 Google Scholar
[45]	Arponen J, Pajanne E 1979 Ann. Phys. 121 343 Google Scholar
[46]	Nieminen R M, Boronski E, Lantto L J 1985 Phys. Rev. B 32 1377 Google Scholar
[47]	Wiktor J, Jomard G, Torrent M 2015 Phys. Rev. B 92 125113 Google Scholar
[48]	Hom T, Kiszenik W, Post B 1975 J. Appl. Crystallogr. 8 457 Google Scholar
[49]	Holloway H, Hass K C, Tamor M A, et al. 1991 Phys. Rev. B 44 7123 Google Scholar
[50]	Zhao Y, Yan F, An Y 2022 Coatings 12 619 Google Scholar
[51]	Uedono A, Fujii S, Morishita N, et al. 1999 J. Phys. Condens. Matter 11 4109 Google Scholar
[52]	Shiryaev A A, Iakoubovskii K, Schut H, et al. 2001 Mater. Sci. Forum 363 – 365 40
[53]	Dannefaer S, Mascher P, Kerr D 1992 Diamond Relat. Mater. 1 407 Google Scholar
[54]	Kršjak V, Sojak S, Slugeň V, et al. 2011 J. Phys. Conf. Ser. 265 012014 Google Scholar
[55]	Dannefaer S, Iakoubovskii K 2008 J. Phys. Condens. Matter 20 235225 Google Scholar
[56]	Puska M J, Lanki P, Nieminen R M 1989 J. Phys. Condens. Matter 1 6081 Google Scholar
[57]	Maier K, Peo M, Saile B, et al. 1979 Philos. Mag. A 40 701 Google Scholar

施引文献

图 1 金刚石正电子湮灭寿命计算模型　(a) 2×2×2的金刚石超胞; (b) 金刚石空位模型; (c) 金刚石空位和掺杂模型

Fig. 1. Calculation model for positron annihilation lifetime of diamond: (a) Diamond supercell of 2×2×2; (b) diamond vacancy model; (c) diamond vacancy and doping models.

下载: 全尺寸图片幻灯片

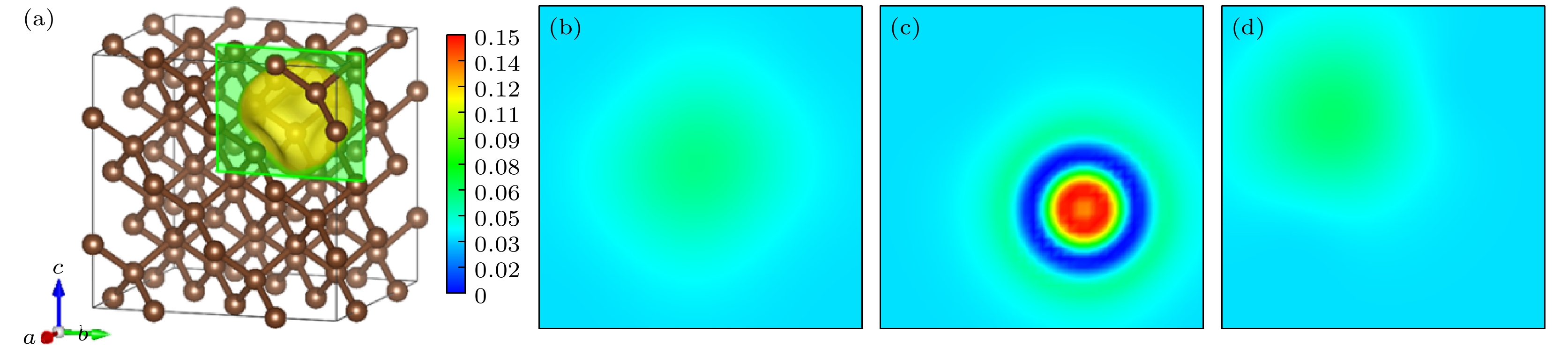
图 2 金刚石空位模型及电子密度图　(a) 金刚石空位模型及切面示意图; (b) 金刚石空位切面二维电子密度图; (c) 金刚石正电子模型及切面示意图; (d) 金刚石空位切面二维电子密度图

Fig. 2. Diamond vacancy model and electron density diagrams: (a) Diamond vacancy model with cross-section; (b) 2D electron density map of the diamond vacancy cross-section; (c) diamond positron model with cross-section; (d) 2D electron density map of the diamond positron cross-section.

下载: 全尺寸图片幻灯片

图 3 金刚石空位与各异质原子的交互作用　(a) 未掺杂金刚石; (b) 掺杂B; (c) 掺杂Cr; (d) 掺杂Mo; (e) 掺杂Ti; (f) 掺杂W; (g) 掺杂Zr

Fig. 3. Interaction of diamond vacancies with various heteroatoms: (a) Pristine diamond; (b) doped with B; (c) doped with Cr; (d) doped with Mo; (e) doped with Ti; (f) doped with W; (g) doped with Zr.

下载: 全尺寸图片幻灯片

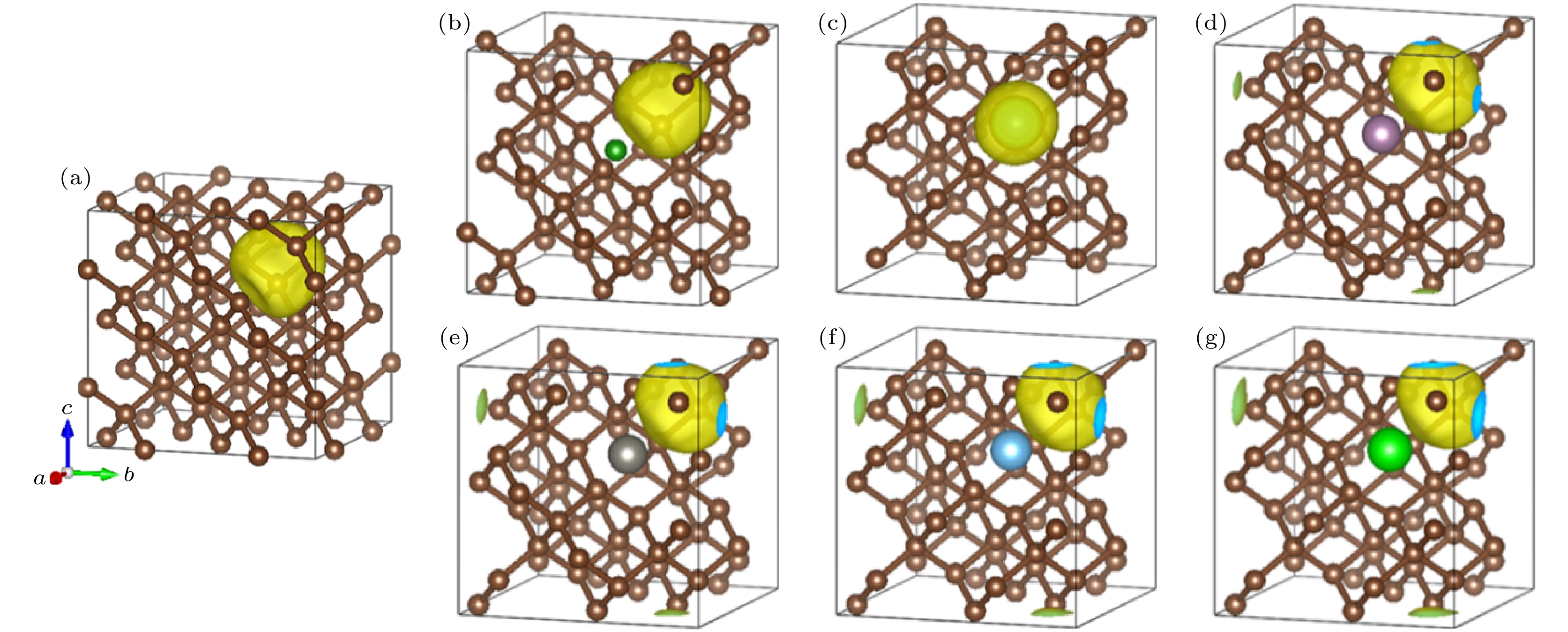
图 4 金刚石超胞掺杂后的二维电子密度图　(a) 金刚石超胞模型和切面示意; (b) 掺杂B; (c) 掺杂Cr; (d) 掺杂Mo; (e) 未掺杂; (f) 掺杂W; (g) 掺杂Ti; (h) 掺杂Zr

Fig. 4. 2D electron density map of diamond supercell after doping: (a) Diamond supercell model and section illustration; (b) doped with B; (c) doped with Cr; (d) doped with Mo; (e) undoped atoms; (f) doped with W; (g) doped with Ti; (h) doped with Zr.

下载: 全尺寸图片幻灯片

图 5 金刚石掺杂后空位的电子局域函数　(a) 金刚石超胞及正电子空位模型; (b) 掺杂B; (c) 掺杂Cr; (d) 掺杂Ti

Fig. 5. Electron local function of vacancies after diamond doping: (a) Diamond supercell and positron vacancy model; (b) doped with B; (c) doped with Cr; (d) doped with Ti.

下载: 全尺寸图片幻灯片

表 1 采用不同正电子–电子交换关联函数和增强因子计算的金刚石正电子湮灭寿命值

Table 1. Diamond positron annihilation lifetime values calculated using different positron electron exchange correlation functions and enhancement factors.

赝势文件	GGA-PBE		LDA-PW			文献
计算方法	Boronski & Nieminen	Sterne & Kaiser	Boronski & Nieminen	Sterne & Kaiser	Puska, Seitsonen, and Nieminen	—
湮灭增强因子	RPA限制和 GGA修正	GGA修正	RPA限制	Sterne & Kaiser	Puska, Seitsonen and Nieminen	—
完美晶体/ps	106.55	108.86	99.8	102.18	107.59	97—115^[31,35,51]
单位/ps	128.85	130.7	119.87	121.79	109.87	120^[53]
电子-电子自洽/ps	—	—	129.54	122.11	122.24	—

下载: 导出CSV

表 2 掺杂B, Cr, Mo, Ti, W和Zr原子后, 金刚石中正电子湮灭寿命值

Table 2. Positron annihilation lifetime values in diamond after doping with B, Cr, Mo, Ti, W, and Zr atoms.

掺杂原子	B	Cr	Mo	W	Ti	Zr	空位
GGA/ps	146.95	156.82	118.21	116.5	116.74	115.74	128.85
LDA/ps	148.57	156.82	119.05	116.5	117.62	115.74	119.87
Ref./ps	142±3^[55]	—	—	—	—	—	120^[53]

下载: 导出CSV

map

[1]	Stachel T, Luth R W 2015 Lithos 220 – 223 200
[2]	Bulanova G P 1995 J. Geochem. Explor. 53 1 Google Scholar
[3]	Wei L, Kuo P K, Thomas R L, et al. 1993 Phys. Rev. Lett. 70 3764 Google Scholar
[4]	Chakraborty P, Xiong G, Cao L, et al. 2018 Carbon 139 85 Google Scholar
[5]	Ciupiński Ł, Kruszewski M J, Grzonka J, et al. 2017 Mater. Des. 120 170 Google Scholar
[6]	Kidalov S V, Shakhov F M 2009 Materials 2 2467 Google Scholar
[7]	May P W 2000 Philos. Trans. R. Soc. London, Ser. A 358 473 Google Scholar
[8]	Liao M 2021 Funct. Diamond 1 29 Google Scholar
[9]	Gomez H, Groves M N, Neupane M R 2021 Carbon Trends 3 100033 Google Scholar
[10]	Pan Y, He X, Ren S, et al. 2018 Vacuum 153 74 Google Scholar
[11]	Soltani H M, Tayebi M 2020 Int. J. Refract. Met. Hard Mater. 87 105172 Google Scholar
[12]	Pillari L K, Bakshi S R, Chaudhuri P, et al. 2020 Adv. Powder Technol. 31 3657 Google Scholar
[13]	Zhang X Y, Xu M, Cao S Z, et al. 2020 Diamond Relat. Mater. 104 107755 Google Scholar
[14]	Jia J, Bai S, Xiong D, et al. 2019 Ceram. Int. 45 10810 Google Scholar
[15]	Liu Z, Zheng S, Lu Z, et al. 2018 Carbon 127 548 Google Scholar
[16]	Wu M, Chang L, Zhang L, et al. 2017 Surf. Coat. Technol. 325 490 Google Scholar
[17]	Contreras Cuevas A, Bedolla Becerril E, Martínez M S, et al. 2018 Metal Matrix Composites (Cham: Springer International Publishing
[18]	Bai G, Li N, Wang X, et al. 2018 J. Alloys Compd. 735 1648 Google Scholar
[19]	Bai G, Wang L, Zhang Y, et al. 2019 Mater. Charact. 152 265 Google Scholar
[20]	Liu X, Sun F, Wang L, et al. 2020 Appl. Surf. Sci. 515 146046 Google Scholar
[21]	Kang Q, He X, Ren S, et al. 2013 J. Alloys Compd. 576 380 Google Scholar
[22]	Che Q L, Chen X K, Ji Y Q, et al. 2015 Mater. Sci. Semicond. Process. 30 104 Google Scholar
[23]	Li J, Zhang H, Wang L, et al. 2016 Composites Part A 91 189 Google Scholar
[24]	Abyzov A M, Kidalov S V, Shakhov F M 2012 Appl. Therm. Eng. 48 72
[25]	He J, Wang X, Zhang Y, et al. 2015 Composites Part B 68 22 Google Scholar
[26]	Wang L, Li J, Bai G, et al. 2019 J. Alloys Compd. 781 800 Google Scholar
[27]	Dannefaer S 2007 Phys. Status Solidi C 4 3605 Google Scholar
[28]	Avalos V, Dannefaer S 2003 Phys. B: Condens. Matter 340 – 342 76
[29]	Siegel R W 1980 Annu. Rev. Mater. Sci. 10 393 Google Scholar
[30]	Tuomisto F, Makkonen I 2013 Rev. Mod. Phys. 85 1583 Google Scholar
[31]	Pu A, Bretagnon T, Kerr D, et al. 2000 Diamond Relat. Mater. 9 1450 Google Scholar
[32]	Sachdeva A, Sudarshan K, Pujari P, et al. 2004 Diamond Relat. Mater. 13 1719 Google Scholar
[33]	Hu X J, Ye J S, Liu H J, et al. 2008 Thin Solid Films 516 1699 Google Scholar
[34]	Jones R 2009 Diamond Relat. Mater. 18 820 Google Scholar
[35]	Fujii S, Nishibayashi Y, Shikata S, et al. 1995 J. Appl. Phys. 78 1510 Google Scholar
[36]	Eseev M, Kuziv I, Kostin A, et al. 2022 Materials 16 203 Google Scholar
[37]	Gonze X, Amadon B, Antonius G, et al. 2020 Comput. Phys. Commun. 248 107042 Google Scholar
[38]	Romero A H, Allan D C, Amadon B, et al. 2020 J. Chem. Phys. 152 124102 Google Scholar
[39]	Gonze X, Jollet F, Abreu Araujo F, et al. 2016 Comput. Phys. Commun. 205 106 Google Scholar
[40]	Gonze X, Amadon B, Anglade P M, et al. 2009 Comput. Phys. Commun. 180 2582 Google Scholar
[41]	Torrent M, Jollet F, Bottin F, et al. 2008 Comput. Mater. Sci. 42 337 Google Scholar
[42]	Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33 Google Scholar
[43]	Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272 Google Scholar
[44]	Boroński E, Nieminen R M 1986 Phys. Rev. B 34 3820 Google Scholar
[45]	Arponen J, Pajanne E 1979 Ann. Phys. 121 343 Google Scholar
[46]	Nieminen R M, Boronski E, Lantto L J 1985 Phys. Rev. B 32 1377 Google Scholar
[47]	Wiktor J, Jomard G, Torrent M 2015 Phys. Rev. B 92 125113 Google Scholar
[48]	Hom T, Kiszenik W, Post B 1975 J. Appl. Crystallogr. 8 457 Google Scholar
[49]	Holloway H, Hass K C, Tamor M A, et al. 1991 Phys. Rev. B 44 7123 Google Scholar
[50]	Zhao Y, Yan F, An Y 2022 Coatings 12 619 Google Scholar
[51]	Uedono A, Fujii S, Morishita N, et al. 1999 J. Phys. Condens. Matter 11 4109 Google Scholar
[52]	Shiryaev A A, Iakoubovskii K, Schut H, et al. 2001 Mater. Sci. Forum 363 – 365 40
[53]	Dannefaer S, Mascher P, Kerr D 1992 Diamond Relat. Mater. 1 407 Google Scholar
[54]	Kršjak V, Sojak S, Slugeň V, et al. 2011 J. Phys. Conf. Ser. 265 012014 Google Scholar
[55]	Dannefaer S, Iakoubovskii K 2008 J. Phys. Condens. Matter 20 235225 Google Scholar
[56]	Puska M J, Lanki P, Nieminen R M 1989 J. Phys. Condens. Matter 1 6081 Google Scholar
[57]	Maier K, Peo M, Saile B, et al. 1979 Philos. Mag. A 40 701 Google Scholar

[1]	吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟. 金刚石氮-空位色心单电子自旋的电场驱动相干控制研究. , 2022, 0(0): . doi: 10.7498/aps.71.20220410
[2]	吴建冬, 程智, 叶翔宇, 李兆凯, 王鹏飞, 田长麟, 陈宏伟. 金刚石氮-空位色心单电子自旋的电场驱动相干控制. , 2022, 71(11): 117601. doi: 10.7498/aps.70.20220410
[3]	李勇, 王应, 李尚升, 李宗宝, 罗开武, 冉茂武, 宋谋胜. 硼硫协同掺杂金刚石的高压合成与电学性能研究. , 2019, 68(9): 098101. doi: 10.7498/aps.68.20190133
[4]	李勇, 李宗宝, 宋谋胜, 王应, 贾晓鹏, 马红安. 硼氢协同掺杂Ib型金刚石大单晶的高温高压合成与电学性能研究. , 2016, 65(11): 118103. doi: 10.7498/aps.65.118103
[5]	王应, 李勇, 李宗宝. B,N协同掺杂金刚石电子结构和光学性质的第一性原理研究. , 2016, 65(8): 087101. doi: 10.7498/aps.65.087101
[6]	贺慧芳, 陈志权. 用正电子湮没研究纳米碲化铋的缺陷及其对热导率的影响. , 2015, 64(20): 207804. doi: 10.7498/aps.64.207804
[7]	房超, 贾晓鹏, 颜丙敏, 陈宁, 李亚东, 陈良超, 郭龙锁, 马红安. 高温高压下氮氢协同掺杂对{100}晶面生长宝石级金刚石的影响. , 2015, 64(22): 228101. doi: 10.7498/aps.64.228101
[8]	颜丙敏, 贾晓鹏, 秦杰明, 孙士帅, 周振翔, 房超, 马红安. 氮氢共掺杂金刚石中氢的典型红外特征峰的表征. , 2014, 63(4): 048101. doi: 10.7498/aps.63.048101
[9]	杨双波. 掺杂浓度及掺杂层厚度对Si均匀掺杂的GaAs量子阱中电子态结构的影响. , 2013, 62(15): 157301. doi: 10.7498/aps.62.157301
[10]	田玉明, 王凯悦, 李志宏, 朱玉梅, 柴跃生, 曾雨顺, 王强. 高能电子照射对金刚石中缺陷电荷状态的影响. , 2013, 62(18): 188101. doi: 10.7498/aps.62.188101
[11]	王凯悦, 朱玉梅, 李志宏, 田玉明, 柴跃生, 赵志刚, 刘开. 氮掺杂金刚石{100}晶面的缺陷发光特性. , 2013, 62(9): 097803. doi: 10.7498/aps.62.097803
[12]	林雪玲, 潘凤春. 氮掺杂的金刚石磁性研究. , 2013, 62(16): 166102. doi: 10.7498/aps.62.166102
[13]	王凯悦, 李志宏, 高凯, 朱玉梅. 电子辐照金刚石的光致发光研究. , 2012, 61(9): 097803. doi: 10.7498/aps.61.097803
[14]	许红霞, 郝颖萍, 韩荣典, 翁惠民, 杜淮江, 叶邦角. 纳米Fe3 O4 颗粒的正电子湮没谱学研究. , 2011, 60(6): 067803. doi: 10.7498/aps.60.067803
[15]	熊涛, 张杰, 陈祥磊, 叶邦角, 杜淮江, 翁惠民. 单晶固体中正电子波函数的计算. , 2010, 59(10): 7374-7377. doi: 10.7498/aps.59.7374
[16]	熊涛, 高传波, 陈祥磊, 周先意, 翁惠民, 曹方宇, 叶邦角, 韩荣典, 杜淮江. Fe3O4-C核壳型纳米纤维的正电子研究. , 2009, 58(10): 6946-6950. doi: 10.7498/aps.58.6946
[17]	李荣斌. 同质与异质外延掺杂CVD金刚石薄膜的结构与性能. , 2009, 58(2): 1287-1292. doi: 10.7498/aps.58.1287
[18]	沈益斌, 周勋, 徐明, 丁迎春, 段满益, 令狐荣锋, 祝文军. 过渡金属掺杂ZnO的电子结构和光学性质. , 2007, 56(6): 3440-3445. doi: 10.7498/aps.56.3440
[19]	李荣斌. 掺杂CVD金刚石薄膜的应力分析. , 2007, 56(6): 3428-3434. doi: 10.7498/aps.56.3428
[20]	胡晓君, 李荣斌, 沈荷生, 何贤昶, 邓文, 罗里熊. 掺杂金刚石薄膜的缺陷研究. , 2004, 53(6): 2014-2018. doi: 10.7498/aps.53.2014

计量

文章访问数: 2773
PDF下载量: 68
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

掺杂B, Cr, Mo, Ti, W, Zr后金刚石中正电子湮灭寿命计算