-
将多孔介质和相变材料复合是提高固液相变储能系统传热性能的有效措施. 本文通过微型计算机断层扫描(micro computed tomography, Micro CT)三维重构得到泡沫铜的数值结构, 采用格子Boltzmann方法对填充泡沫铜复合相变材料的方腔融化过程进行孔隙尺度模拟研究, 讨论不同Rayleigh数以及热导率下, 泡沫铜骨架中空对泡沫铜内融化过程的影响. 结果表明, 中空骨架泡沫铜相比实心骨架泡沫铜, 融化前期换热强度更低、相变材料的融化更慢、储能效率η更高. 与泡沫铜骨架相比, 通过骨架中空区进入方腔的热流量可以忽略不计; 随Fourier数的增大, 泡沫铜的传热增强效率ζ会因为导热和自然对流的竞争而出现先上升后下降然后再上升的现象; 当Rayleigh数减小时, 储能效率η提高, 传热增强效率ζ随Fourier数的变化趋于平缓, 中空骨架泡沫铜和实心骨架泡沫铜对应的传热增强效率ζ的差距减小; 泡沫铜骨架和相变材料热导率之比越大, 融化结束时刻储能效率η越低, 中空骨架泡沫铜和实心骨架泡沫铜对应的传热增强效率ζ的差距越小.The compositing of porous medium and phase change material is an effective way to improve the heat transfer performance of solid-liquid phase change energy storage system. In this paper, we reconstruct the three-dimensional numerical structure of the copper foam by using the micro computed tomography, and then conduct the pore-scale numerical simulation of the melting process in a cubic cavity filled with the phase change material comprised of the copper foam via the lattice Boltzmann method. The effects of the hollow skeleton on the melting process are discussed in detail under different Rayleigh numbers and ratios of thermal conductivity of the copper foam to that of the phase change material. The results show that the hollow skeleton copper foam possesses a lower average Nusselt number along the left wall at the early stage of the melting process, a slower melting rate, and a higher energy storage efficiency than the solid skeleton copper foam. Comparing with the skeleton region of the copper foam, the heat transfer rate entering the cubic cavity through the hollow region of the skeleton is almost negligible. Because of the competition between heat conduction and natural convection, the heat transfer enhancement efficiency of copper foam first increases, then decreases, and then increases again with the increase of the Fourier number. When the Rayleigh number decreases, the energy storage efficiency increases, and the natural convection also weakens. Meanwhile, the fluctuation of the heat transfer enhancement efficiency decreases as the Fourier number increases, and the gap of the heat transfer enhancement efficiency between the hollow skeleton copper foam and the solid skeleton copper foam becomes smaller. When the ratio of the thermal conductivity of the copper foam skeleton to that of the phase change material increases, the energy storage efficiency is relatively high at the early stage of the melting process but becomes relatively low when the melting process is completed. With a larger thermal conductivity ratio, the heat transfer rate entering the cubic cavity through the skeleton region of the copper foam becomes dominant, which reduces the effect of the hollow skeleton on heat transfer, and thus the gap of the heat transfer enhancement efficiency between the hollow skeleton copper foam and the solid skeleton copper foam becomes relatively small.
-
Keywords:
- hollow skeleton /
- copper foam /
- micro computed tomography /
- melting
[1] Zhang N, Yuan Y P, Cao X L, Du Y X, Zhang Z L, Gui Y W 2018 Adv. Eng. Mater. 20 1700753
Google Scholar
[2] Vélez C, Khayet M, Ortiz de Zárate J M 2015 Appl. Energy 143 383
Google Scholar
[3] Su W G, Darkwa J, Kokogiannakis G 2015 Renew. Sust. Energ. Rev. 48 373
Google Scholar
[4] Ren Q L, Chan C L 2016 Int. J. Heat Mass Transfer 100 522
Google Scholar
[5] Arıcı M, Tütüncü E, Kan M, Karabay H 2017 Int. J. Heat Mass Transfer 104 7
Google Scholar
[6] Luo K, Yao F J, Yi H L, Tan H P 2015 Appl. Therm. Eng. 86 238
Google Scholar
[7] 龚玮, 杨震, 段远源 2014 太阳能学报 35 1682
Google Scholar
Gong W, Yang Z, Duan Y Y 2014 Acta Energ. Sol. Sin. 35 1682
Google Scholar
[8] Ren Q L, Wang Z X, Lai T, Zhang J F, Qu Z G 2021 Appl. Therm. Eng. 189 116618
Google Scholar
[9] Yang X H, Bai Q S, Guo Z X, Niu Z Y, Yang C, Jin L W, Lu T J, Yan J Y 2018 Appl. Energy 229 700
Google Scholar
[10] 冯妍卉, 冯黛丽, 褚福强, 邱琳, 孙方远, 林林, 张欣欣 2022 71 016501
Google Scholar
Feng Y H, Feng D L, Chu F Q, Qiu L, Sun F Y, Lin L, Zhang X X 2022 Acta Phys. Sin. 71 016501
Google Scholar
[11] 李静, 李绍伟, 蔡迪, 廖燕宁 2021 70 040503
Google Scholar
Li J, Li S W, Cai D, Liao Y N 2021 Acta Phys. Sin. 70 040503
Google Scholar
[12] Xiao X, Zhang P, Li M 2013 Appl. Energy 112 1357
Google Scholar
[13] 张贝豪, 郑林 2020 69 164401
Google Scholar
Zhang B H, Zheng L 2020 Acta Phys. Sin. 69 164401
Google Scholar
[14] Huang X P, Sun C, Chen Z Q, Han Y S 2021 Int. J. Therm. Sci. 170 107151
Google Scholar
[15] Zhang Z Q, He X D 2017 Appl. Therm. Eng. 113 298
Google Scholar
[16] Ghahremannezhad A, Xu H, Salimpour M R, Wang P, Vafai K 2020 Appl. Therm. Eng. 179 115731
Google Scholar
[17] Li X Y, Zhu Z L, Xu Z R, Ma T, Zhang H, Liu J, Wang X, Wang Q W 2019 Appl. Energy 254 113507
Google Scholar
[18] 张士卫 2016 粉末冶金技术 34 222
Google Scholar
Zhang S W 2016 Powder Metall. Technol. 34 222
Google Scholar
[19] 张秋利, 杨志懋, 丁秉钧 2009 有色金属 61 30
Google Scholar
Zhang Q L, Yang Z M, Ding B J 2009 Nonferrous Met. 61 30
Google Scholar
[20] He Y L, Liu Q, Li Q, Tao W Q 2019 Int. J. Heat Mass Transfer 129 160
Google Scholar
[21] Huang R Z, Wu H Y, Adams N A 2021 Phys. Rev. Lett. 126 244501
Google Scholar
[22] 娄钦, 黄一帆, 李凌 2019 68 214702
Google Scholar
Lou Q, Huang Y F, Li L 2019 Acta Phys. Sin. 68 214702
Google Scholar
[23] Huang R Z 2017 Ph. D. Dissertation (Shanghai: Shanghai Jiao Tong University) (in Chinese)
[24] d’Humières D 2002 Philos. Trans. R. Soc. London, Ser. A 360 437
Google Scholar
[25] Huang R Z, Wu H Y 2016 J. Comput. Phys. 315 65
Google Scholar
-
图 1 (a) 泡沫铜的实物图; (b) SEM图; (c) 骨架中空区局部放大SEM图
Fig. 1. (a) Physical image of copper foam; (b) SEM image; (c) enlarged SEM image of the hollow skeleton.
图 2 泡沫铜Micro CT图阈值分区处理
Fig. 2. Threshold partition processing of Micro CT image of copper foam.
图 3 (a) 泡沫铜的真实数值结构; (b) 骨架中空区域分布
Fig. 3. (a) Actual numerical structure; (b) distribution of hollow regions in the skeleton of copper foam.
图 4 填充泡沫铜复合相变材料的三维方腔左壁面加热融化示意图
Fig. 4. Schematic of melting in a three-dimensional cubic cavity filled with phase change material embedded with copper foam and heated by the left wall.
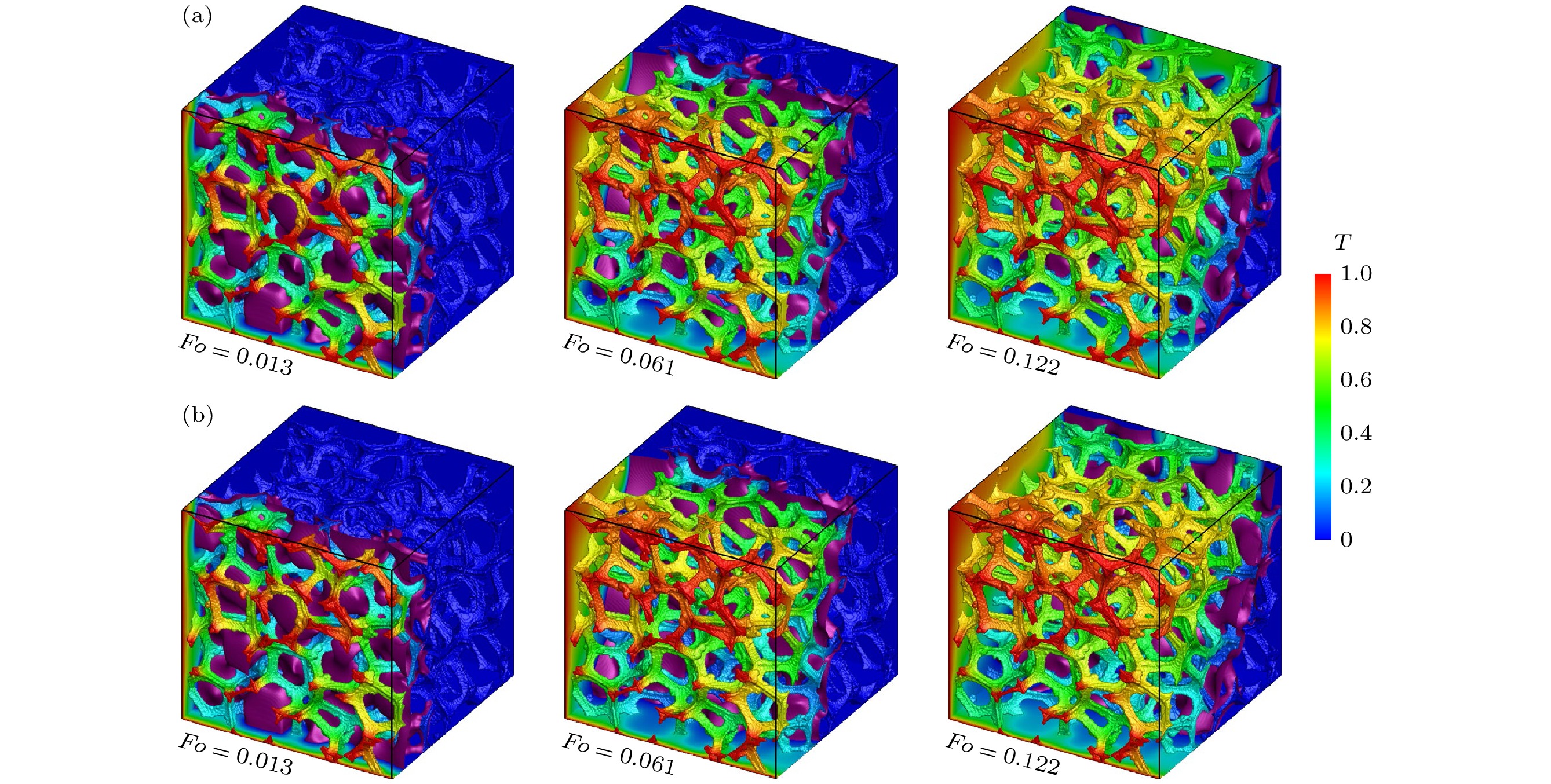
图 5 融化过程中固液相界面(紫色曲面)位置, 以及右壁面(
$x = 1$ )、后壁面($y = 1$ )、下壁面($z = 0$ )和骨架表面的温度分布 (a) SSCF; (b) HSCFFig. 5. Evolution of the solid-liquid phase interface (the purple surface), the temperature distributions on the right (
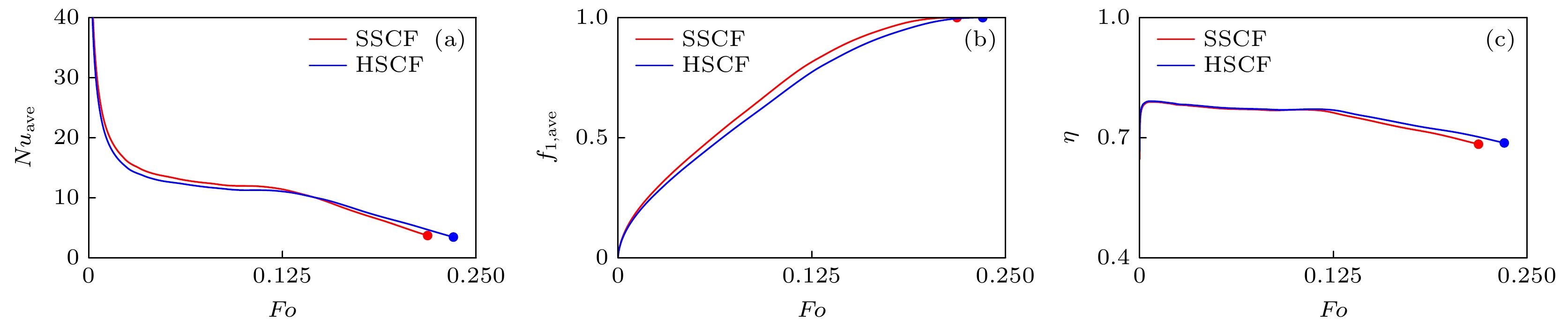
$x = 1$ ), back ($y = 1$ ), bottom ($z = 0$ ) walls and skeleton surface during the melting process: (a) SSCF; (b) HSCF.
图 6
$Fo = 0.061$ 时, 方腔左壁面的热流密度分布 (a) SSCF; (b) HSCFFig. 6. Heat flux distribution on the left wall of the cubic cavity at
$Fo = 0.061$ : (a) SSCF; (b) HSCF.
图 7 不同因素随Fourier数Fo的变化 (a) 左壁面平均Nusselt数
$N{u_{{\text{ave}}}}$ ; (b) 方腔内平均液相率${f_{{\text{l, ave}}}}$ ; (c) 储能效率ηFig. 7. Variations of different factors with the Fourier number Fo: (a) Average Nusselt number
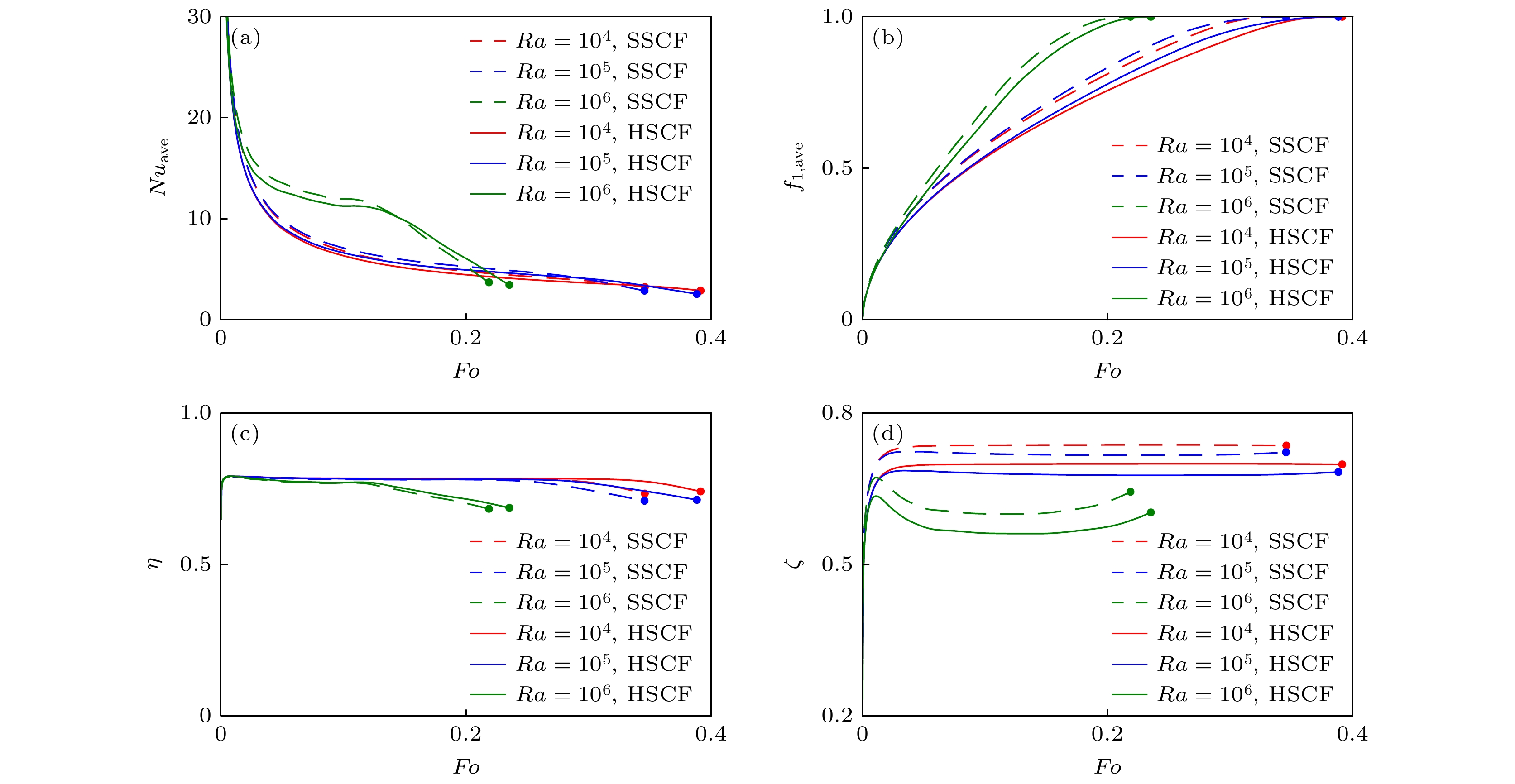
$N{u_{{\text{ave}}}}$ along the left wall; (b) average liquid fraction over the whole cavity${f_{{\text{l, ave}}}}$ ; (c) energy storage efficiency η.
图 8 SSCF (a)和HSCF (b)对应左壁面不同区域的热流量Φ; (c) 泡沫铜传热增强效率ζ随Fourier数Fo的变化
Fig. 8. Variations of the heat transfer rate Φ of different regions of the left wall corresponding to SSCF (a) and HSCF (b); (c) heat transfer enhancement efficiency of copper foam ζ with the Fourier number Fo.
图 9 不同Ra时, 不同因素随Fourier数Fo的变化 (a) 左壁面平均Nusselt数; (b) 方腔内平均液相率
${f_{{\text{l, ave}}}}$ ; (c) 储能效率η; (d)泡沫铜传热增强效率ζFig. 9. Variations of different factors with the Fourier number Fo at different Ra: (a) Average Nusselt number along the left wall; (b) average liquid fraction over the whole cavity
${f_{{\text{l,ave}}}}$ ; (c) energy storage efficiency η; (d) heat transfer enhancement efficiency of copper foam ζ .
图 10 不同
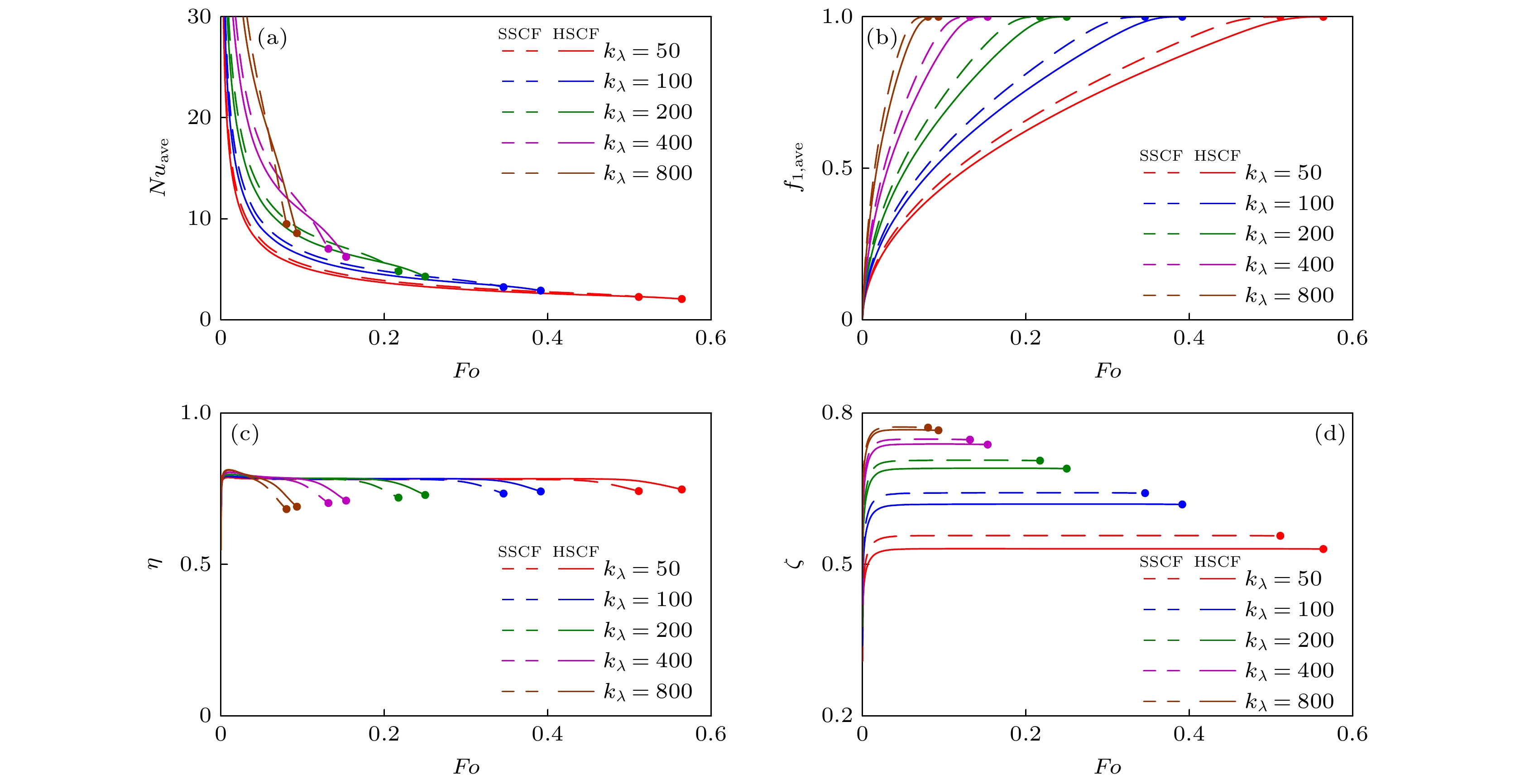
${k_\lambda }$ 时, 不同因素随Fourier数Fo的变化 (a) 左壁面平均Nusselt数$N{u_{{\text{ave}}}}$ ; (b) 方腔内平均液相率${f_{{\text{l,ave}}}}$ ; (c) 储能效率η; (d) 泡沫铜传热增强效率ζFig. 10. Variations of different factors with the Fourier number Fo at different
${k_\lambda }$ : (a) Average Nusselt number along the left wall$N{u_{{\text{ave}}}}$ ; (b) average liquid fraction over the whole cavity${f_{{\text{l, ave}}}}$ ; (c) energy storage efficiency η; (d) heat transfer enhancement efficiency of copper foam ζ. -
[1] Zhang N, Yuan Y P, Cao X L, Du Y X, Zhang Z L, Gui Y W 2018 Adv. Eng. Mater. 20 1700753
Google Scholar
[2] Vélez C, Khayet M, Ortiz de Zárate J M 2015 Appl. Energy 143 383
Google Scholar
[3] Su W G, Darkwa J, Kokogiannakis G 2015 Renew. Sust. Energ. Rev. 48 373
Google Scholar
[4] Ren Q L, Chan C L 2016 Int. J. Heat Mass Transfer 100 522
Google Scholar
[5] Arıcı M, Tütüncü E, Kan M, Karabay H 2017 Int. J. Heat Mass Transfer 104 7
Google Scholar
[6] Luo K, Yao F J, Yi H L, Tan H P 2015 Appl. Therm. Eng. 86 238
Google Scholar
[7] 龚玮, 杨震, 段远源 2014 太阳能学报 35 1682
Google Scholar
Gong W, Yang Z, Duan Y Y 2014 Acta Energ. Sol. Sin. 35 1682
Google Scholar
[8] Ren Q L, Wang Z X, Lai T, Zhang J F, Qu Z G 2021 Appl. Therm. Eng. 189 116618
Google Scholar
[9] Yang X H, Bai Q S, Guo Z X, Niu Z Y, Yang C, Jin L W, Lu T J, Yan J Y 2018 Appl. Energy 229 700
Google Scholar
[10] 冯妍卉, 冯黛丽, 褚福强, 邱琳, 孙方远, 林林, 张欣欣 2022 71 016501
Google Scholar
Feng Y H, Feng D L, Chu F Q, Qiu L, Sun F Y, Lin L, Zhang X X 2022 Acta Phys. Sin. 71 016501
Google Scholar
[11] 李静, 李绍伟, 蔡迪, 廖燕宁 2021 70 040503
Google Scholar
Li J, Li S W, Cai D, Liao Y N 2021 Acta Phys. Sin. 70 040503
Google Scholar
[12] Xiao X, Zhang P, Li M 2013 Appl. Energy 112 1357
Google Scholar
[13] 张贝豪, 郑林 2020 69 164401
Google Scholar
Zhang B H, Zheng L 2020 Acta Phys. Sin. 69 164401
Google Scholar
[14] Huang X P, Sun C, Chen Z Q, Han Y S 2021 Int. J. Therm. Sci. 170 107151
Google Scholar
[15] Zhang Z Q, He X D 2017 Appl. Therm. Eng. 113 298
Google Scholar
[16] Ghahremannezhad A, Xu H, Salimpour M R, Wang P, Vafai K 2020 Appl. Therm. Eng. 179 115731
Google Scholar
[17] Li X Y, Zhu Z L, Xu Z R, Ma T, Zhang H, Liu J, Wang X, Wang Q W 2019 Appl. Energy 254 113507
Google Scholar
[18] 张士卫 2016 粉末冶金技术 34 222
Google Scholar
Zhang S W 2016 Powder Metall. Technol. 34 222
Google Scholar
[19] 张秋利, 杨志懋, 丁秉钧 2009 有色金属 61 30
Google Scholar
Zhang Q L, Yang Z M, Ding B J 2009 Nonferrous Met. 61 30
Google Scholar
[20] He Y L, Liu Q, Li Q, Tao W Q 2019 Int. J. Heat Mass Transfer 129 160
Google Scholar
[21] Huang R Z, Wu H Y, Adams N A 2021 Phys. Rev. Lett. 126 244501
Google Scholar
[22] 娄钦, 黄一帆, 李凌 2019 68 214702
Google Scholar
Lou Q, Huang Y F, Li L 2019 Acta Phys. Sin. 68 214702
Google Scholar
[23] Huang R Z 2017 Ph. D. Dissertation (Shanghai: Shanghai Jiao Tong University) (in Chinese)
[24] d’Humières D 2002 Philos. Trans. R. Soc. London, Ser. A 360 437
Google Scholar
[25] Huang R Z, Wu H Y 2016 J. Comput. Phys. 315 65
Google Scholar
下载:
计量
- 文章访问数: 2639
- PDF下载量: 72
- 被引次数: 0
