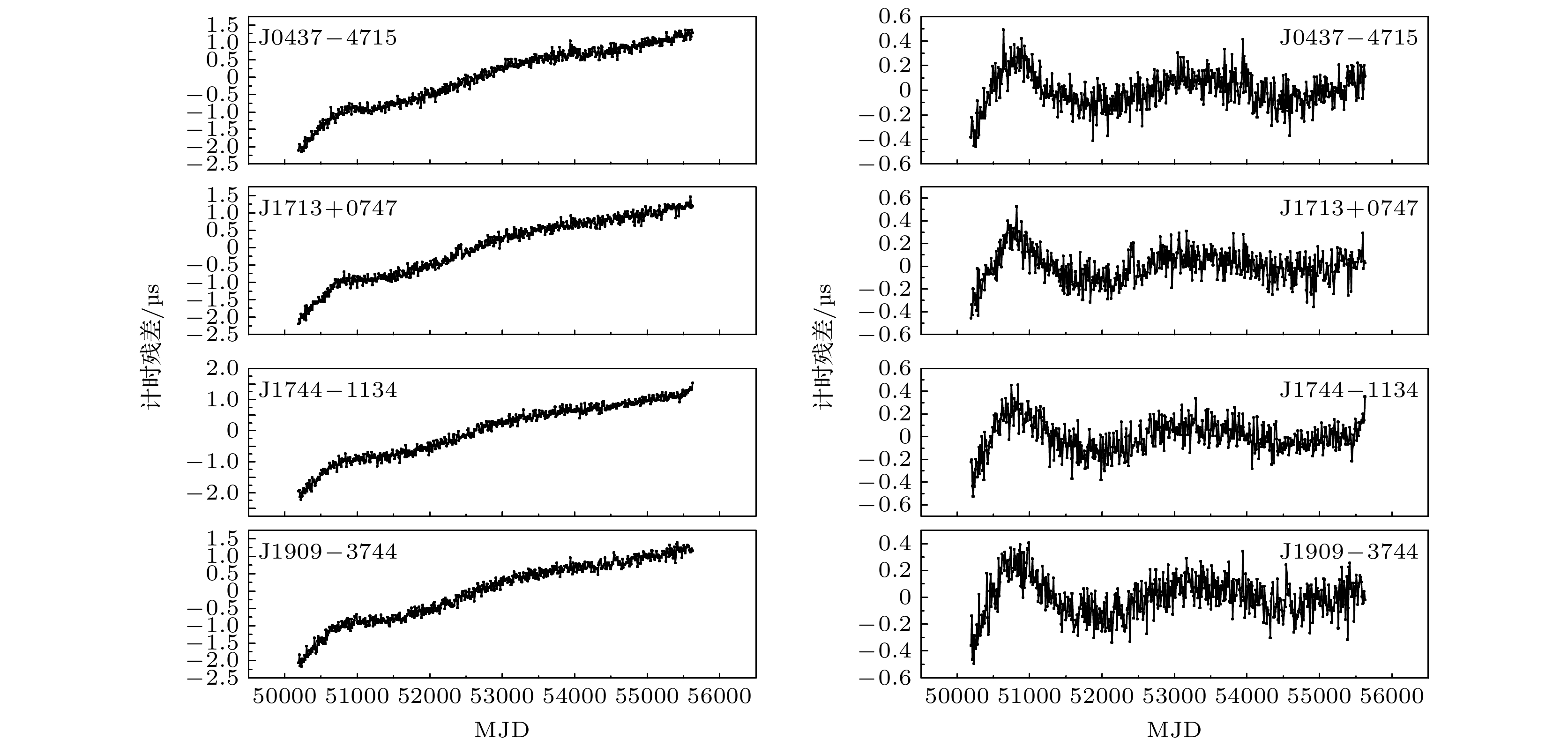
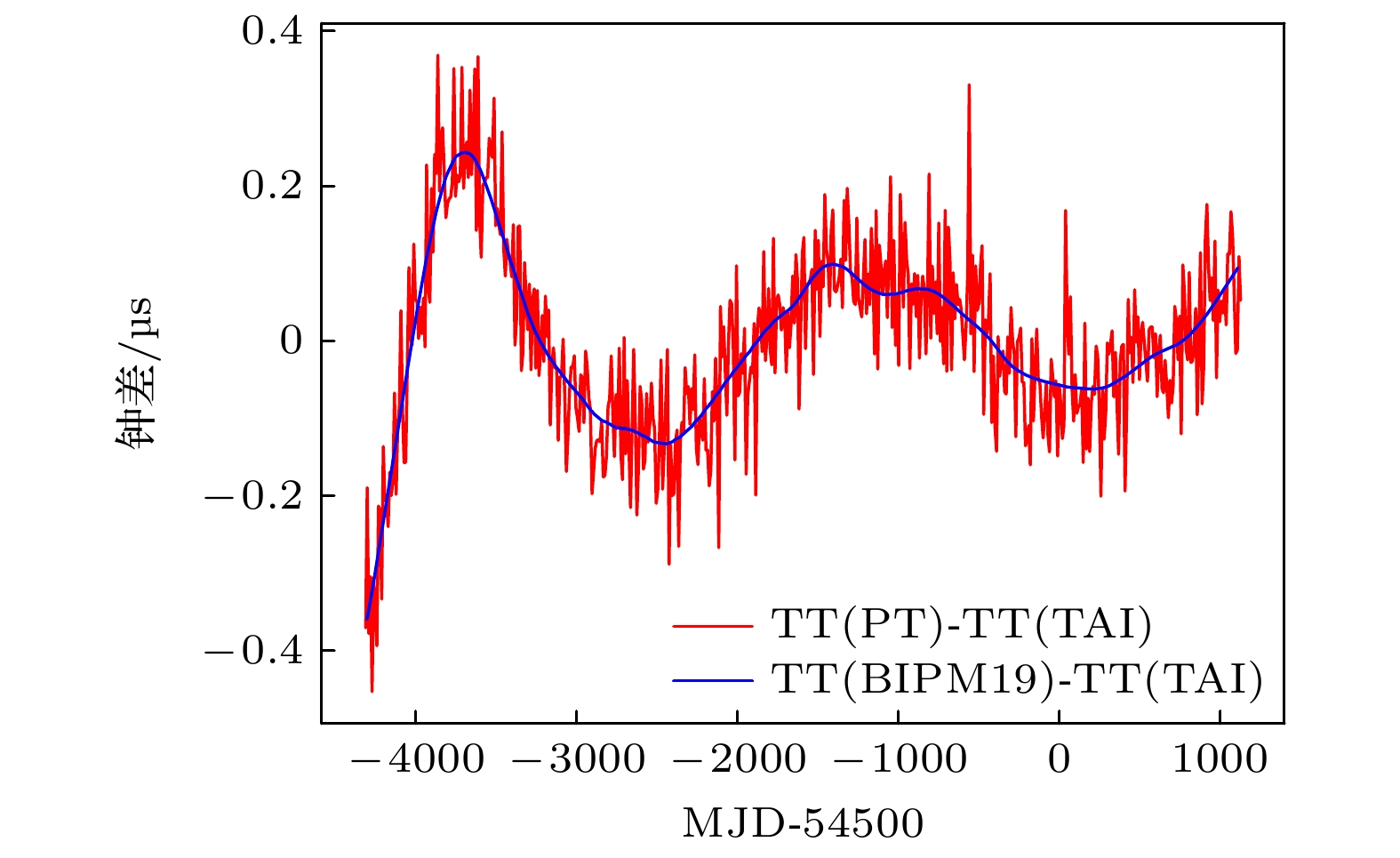
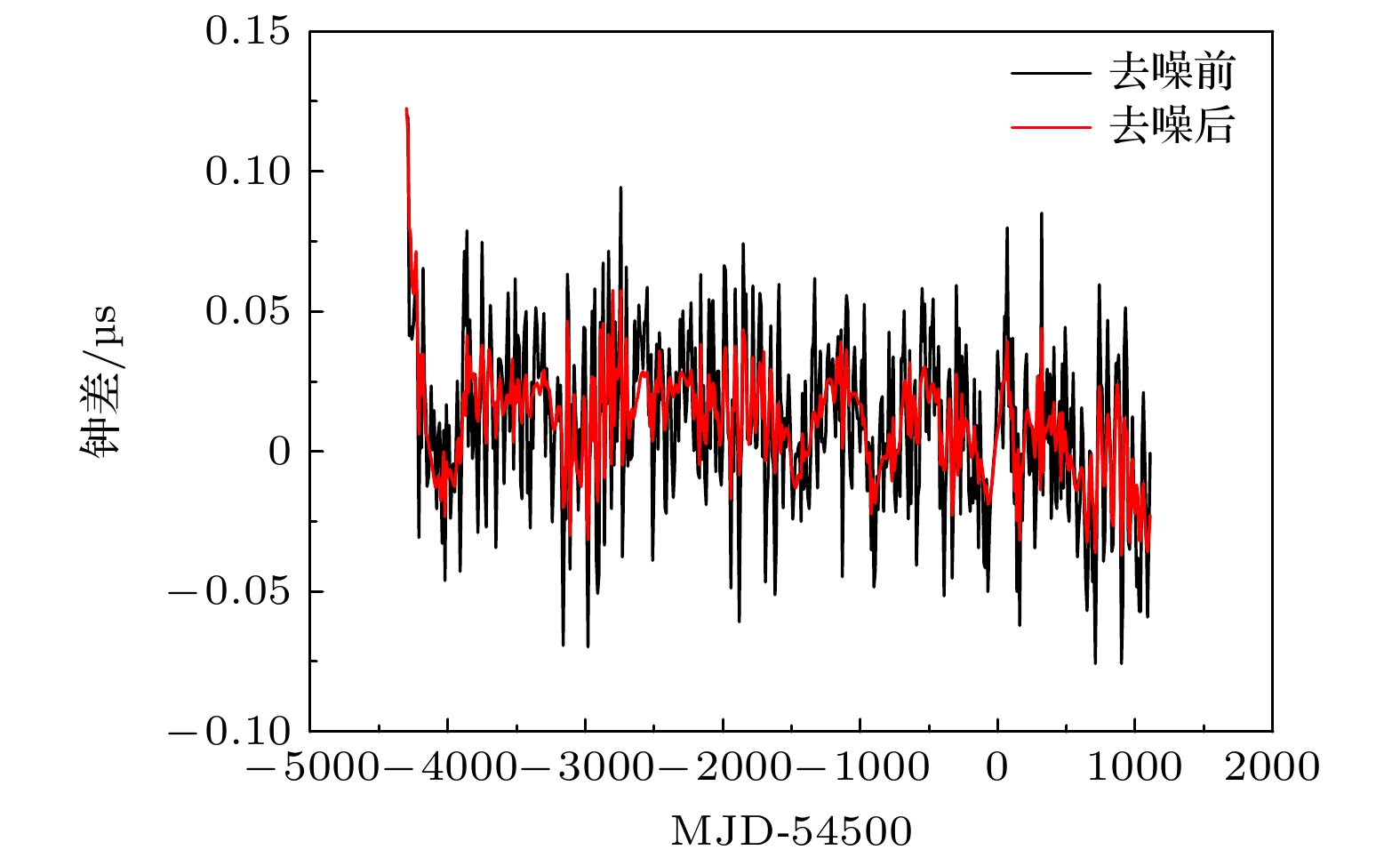
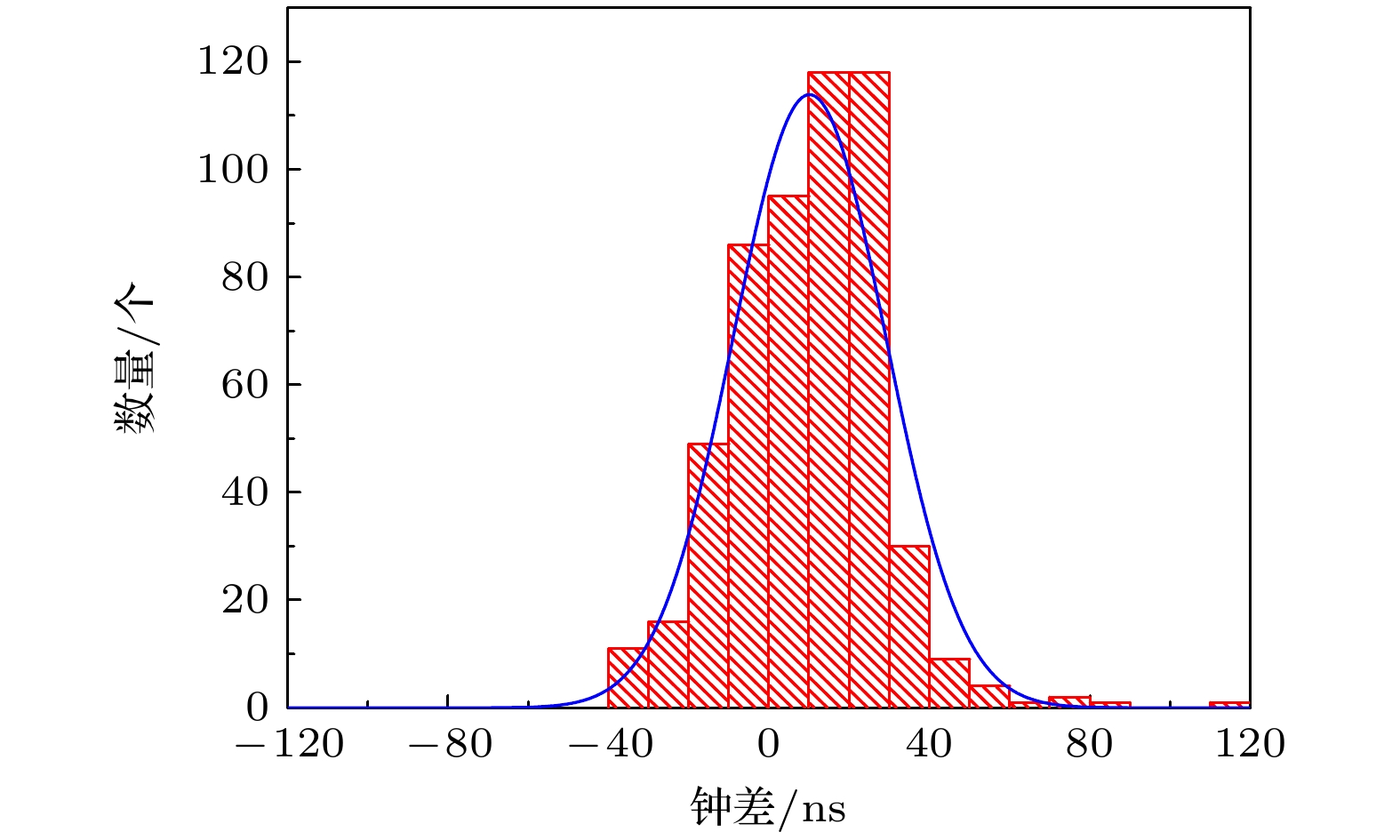
-
脉冲星时(pulsar time, PT)具有较高的长期稳定性, 其与原子时(atomic time, AT)的建立属于两个完全不同的物理过程. 因此, 脉冲星时可作为原子时波动的一种独立检验方式. 本文结合真实钟差数据，展示了基于脉冲星时的原子时波动检验结果. 首先, 给出了Parkes脉冲星计时阵(Parkes pulsar timing array, PPTA)发布数据中四颗毫秒脉冲星的计时结果. 为进行原子时波动的检验, 利用四颗脉冲星的计时模型参数, 仿真生成以地球时(terrestrial time, TT) (BIPM19)为参考的脉冲到达时间(pulse times of arrival, TOAs)数据, 然后将参考时由TT (BIPM19)改为TT (TAI). 基于此, 分别采用经典加权平均算法与维纳(Wiener)滤波算法提取了原子时相对于脉冲星时的波动. 将两种方法得到的检验结果进行对比, 结果表明Wiener滤波算法对原子时波动的提取效果优于加权平均算法. 本文在Wiener滤波算法提取钟差信号的基础上加入了小波阈值去噪算法以扣除高频噪声, 去噪后PT更接近于TT (BIPM19), 进一步提高了PT对AT波动的检测能力. 对于TOA测量精度为100 ns的情况, PT与TT (BIPM19)的差值大致保持在40 ns以内. 本文是在给定TOA测量精度的前提下研究进一步提高PT精度的方法, 对下一步PT更加有效的守时应用具有重要意义.Pulsar time (PT) has high long-term stability, and its establishment process is completely different from that of atomic time (AT). Therefore, pulsar-based time scale can be used as an independent test for the fluctuation of atomic time scale. In this paper, the test results of the fluctuation of atomic time using pulsar time are presented in combination with the real clock difference data. In order to test the fluctuation of atomic time, the timing model parameters of four pulsars are used to simulate the pulse times of arrival (TOAs) data with TT(BIPM19) as the reference, and then the reference time is changed from TT(BIPM19) to TT(TAI). Based on this, the classical weighted average algorithm and the Wiener filtering algorithm are used to extract the variations of the atomic time relative to the pulsar time. The test results obtained by the two methods are compared, and it shows that the Wiener filtering algorithm is better than the weighted average algorithm for the extraction of the fluctuation of the atomic time. The wavelet threshold denoising method is added to the clock difference signal extracted by the Wiener filtering algorithm to deduct the high-frequency noise. After denoising, PT is closer to TT(BIPM19), which further improves the ability of PT to detect the fluctuation of AT. For the TOA measurement accuracy of 100 ns, the difference between PT and TT(BIPM19) can be kept roughly within 40 ns. This paper studies the method of further improving the accuracy of PT under the premise of given TOA measurement accuracy, which is of great significance for the next step to use PT for more effective application of time keeping.
-
Keywords:
- pulsar time /
- atomic time /
- clock difference /
- timing residual
[1] Allan D W 1987 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 34 647
Google Scholar
[2] Panfilo G, Arias E F 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 140
[3] Kaplan G H 2006 arXiv: 0602086[astro-ph]
[4] Guinot B 1988 Astron. Astrophys. 192 370
[5] Petit G 2003 Proceedings of the 35th Annual Precise Time and Time Interval Systems and Applications Meeting San Diego, California, December 2–4, 2003 p317
[6] Gao Z F, Wang N, Shan H, Li X D, Wang W 2017 Astrophys. J. 849 19
Google Scholar
[7] Gao Z F, Li X D, Wang N, Yuan J P, Wang P, Peng Q H, Du Y J 2016 Mon. Not. R. Astron. Soc. 456 55
Google Scholar
[8] Fu G Z, Xing C C, Wang N 2020 Eur. Phys. J. C 80 582
Google Scholar
[9] Wang H, Gao Z F, Jia H Y, Wang N, Li X 2020 Universe 6 63
Google Scholar
[10] Zhu C, Gao Z F, Li X D, Wang N, Yuan J P, Peng Q 2016 Mod. Phys. Lett. A 31 1650070
[11] Yan F Z, Gao Z F, Yang W S, Dong A J 2021 Astron. Nachr. 342 249
Google Scholar
[12] Gao Z F, Wang N, Peng Q H, Li X D, Du Y J 2013 Mod. Phys. Lett. A 28 1350138
[13] Gao Z F, Song D L, Li X, Shan H, Wang N 2019 Astron. Nachr. 340 241
Google Scholar
[14] Deng Z L, Gao Z F, Li X D, Shao Y 2020 Astrophys. J. 892 4
Google Scholar
[15] Deng Z L, Li X D, Gao Z F, Shao Y 2021 Astrophys. J. 909 174
Google Scholar
[16] Lorimer D R, Kramer M 1965 Handbook of Pulsar Astronomy (New York: Cambridge University Press) pp32–34
[17] Coles W, Hobbs G, Champion D J, Manchester R N, Verbiest J P W 2011 Mon. Not. R. Astron. Soc. 418 561
Google Scholar
[18] Hobbs G, Guo L, Caballero R N, Coles W, Lee K J, Manchester R N, Reardon D J, Matsakis D, Tong M L, Arzoumanian Z, Bailes M, Bassa C G, Bhat N D R, Brazier A, Burke-Spolaor S, Champion D J, Chatterjee S, Cognard I, Dai S, Desvignes G, Dolch T, Ferdman R D, Graikou E, Guillemot L, Janssen G H, Keith M J, Kerr M, Kramer M, Lam M T, Liu K, Lyne A, Lazio T J W, Lynch R, McKee J W, McLaughlin M A, Mingarelli C M F, Nice D J, Osłowski S, Pennucci T T, Perera B B P, Perrodin D, Possenti A, Russell C J, Sanidas S, Sesana A, Shaifullah G, Shannon R M, Simon J, Spiewak R, Stairs I H, Stappers B W, Swiggum J K, Taylor S R, Theureau G, Toomey L, van Haasteren R, Wang J B, Wang Y, Zhu X J 2020 Mon. Not. R. Astron. Soc. 491 5951
Google Scholar
[19] Gao F, Tong M L, Gao Y P, Yang T G, Zhao C S 2019 Res. Astron. Astrophys. 19 100
Google Scholar
[20] Petit G, Tavella P 1985 Astron. Astrophys. 308 290
[21] Hobbs G, Coles W, Manchester R N, Keith M J, Shannon R M, Chen D, Bailes M, Bhat N D R, Burke-Spolaor S, Champion D, Chaudhary A, Hotan A, Khoo J, Kocz J, Levin Y, Oslowski S, Preisig B, Ravi V, Reynolds J E, Sarkissian J, van Straten W, Verbiest J P W, Yardley D, You X P 2012 Mon. Not. R. Astron. Soc. 427 2780
Google Scholar
[22] 仲崇霞, 杨廷高 2009 天文学报 50 425
Google Scholar
Zhong C X, Yang T G 2009 Acta Astronom. Sin. 50 425
Google Scholar
[23] Yang T G, Tong M L, Gao Y P 2022 Res. Astron. Astrophys. 22 105012
Google Scholar
[24] BIPM Time Department https://webtai.bipm.org/ftp/pub/tai/data/[2022-10-07]
[25] Hobbs G 2013 Classical Quant. Grav. 30 224007
Google Scholar
[26] PPTA Data Release https://doi.org/10.4225/08/534CC21379C12[2022-10-08]
[27] Hobbs G B, Edwards R T, Manchester R N 2006 Mon. Not. R. Astron. Soc. 369 655
Google Scholar
[28] Manchester R N, Hobbs G, Bailes M, Coles W A, van Straten W, Keith M J, Shannon R M, Bhat N D R, Brown A, Burke-Spolaor S G, Champion D J, Chaudhary A, Edwards R T, Hampson G, Hotan A W, Jameson A, Jenet F A, Kesteven M J, Khoo J, Kocz J, Maciesiak K, Oslowski S, Ravi V, Reynolds J R, Sarkissian J M, Verbiest J P W, Wen Z L, Wilson W E, Yardley D, Yan W M, You X P 2012 Publ. Astron. Soc. Pac 30 17
[29] Wiener N, Mathematician C 1949 Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications (Massachusetts: MIT press) pp1043–1054
[30] Rodin A E 2008 Mon. Not. R. Astron. Soc. 387 1583
Google Scholar
[31] Noor M A 1993 J. Optim. Theory Appl. 79 197
Google Scholar
[32] Kopeikin S M 1999 Mon. Not. R. Astron. Soc. 305 563
Google Scholar
[33] 童明雷, 杨廷高, 赵成仕, 高玉平 2017 中国科学: 物理学 力学 天文学 47 099503
Google Scholar
Tong M L, Yang T G, Zhao C S, Gao Y P 2017 Sci. Sin-Phys. Mech. Astron. 47 099503
Google Scholar
[34] Zhao R M, Cui H 2015 Proceedings of the 14th International Symposium on Plasma Chemistry Sousse, Tunisia, December 18–20, 2015 p1
[35] Shan H, Yuan J P, Wang N, Wang Z 2022 Astrophys. J. 935 117
Google Scholar
[36] 王英红, 王冬霞, 杨洪升 2004 辽宁工学院学报 24 7
Wang Y H, Wang D X, Yang H S 2004 Journal of Liaoning Institute of Technology 24 7
[37] Cameron A D, Li D, Hobbs G, Zhang L, Miao C C, Wang J B, Yuan M, Wang S, Jacobs Corban G, Cruces M, Dai S, Feng Y, Han J, Kaczmarek J F, Niu J R, Pan Z C, Qian L, Tao Z Z, Wang P, Wang S Q, Xu H, Xu R X, Yue Y L, Zhang S B, Zhi Q J, Zhu W W, Champion D J, Kramer M, Zhou S Q, Qiu K P, Zhu M 2020 Mon. Not. R. Astron. Soc. 495 3515
Google Scholar
[38] Han J L, Wang C, Wang P F, Wang T, Zhou D J, Sun J H, Yan Y, Su W Q, Jing W C, Chen X, Gao X Y, Hou L G, Xu J, Lee K J, Wang N, Jiang P, Xu R X, Yan J, Gan H Q, Guan X, Huang W J, Jiang J C, Li H, Men Y P, Sun C, Wang B J, Wang H G, Wang S Q, Xie J T, Xu H, Yao R, You X P, Yu D J, Yuan J P, Yuen R, Zhang C F, Zhu Y 2021 Res. Astron. Astrophys. 21 107
Google Scholar
-
图 2 以TAI为参考时四颗星的拟合前后计时残差
Fig. 2. Pre-fit and post-fit timing residuals of four pulsars when the reference time scale is TAI
图 3 经典加权平均算法计算的TT (PT)-TT (TAI)
Fig. 3. TT (PT)-TT (TAI) calculated by classical weighted average algorithm
图 4 Wiener 滤波算法计算的TT (PT)-TT (TAI)
Fig. 4. TT (PT)-TT (TAI) calculated by Wiener filtering algorithm
图 7 TT (PT)-TT (TAI)经小波阈值去噪前后的对比图
Fig. 7. TT (PT)-TT (TAI) before and after processing by wavelet threshold denoising method
图 8 小波阈值去噪前后TT (PT)相对于TT (BIPM19) 的变化
Fig. 8. Changes of TT (PT) relative to TT (BIPM19) before and after wavelet threshold denoising
图 9 小波阈值去噪后TT (PT)-TT (BIPM19)的分布图
Fig. 9. Distribution map of TT (PT)-TT (BIPM19) after processing by wavelet threshold denoising method
参数 含义 数值 PSRJ 脉冲星名称 J0437-4715 J1713+0747 J1744-1134 J1909-3744 RAJ/(hh:mm:ss.sss) J2000赤经 04:37:15.8961766 17:13:49.5327233 17:44:29.4057898 19:09:47.4346727 DECJ/(°) J2000赤纬 –47:15:09.11071 +07:47:37.49783 –11:34:54.68134 –37:44:14.46677 F0/$\rm{s}^{-1}$ 自转频率 173.6879458121841 218.8118404348010 245.4261197130545 339.3156872882437 F1/$\rm{s}^{-2}$ 自转频率的一阶导数 –1.728362 × 10–15 –4.08381×10–16 –5.38183 × 10–16 –1.614845 × 10–15 PEPOCH/MJD 周期确定的历元 54500 54500 54500 54500 DM/($\rm{cm^{-3}\cdot pc}$) 色散 2.6449 15.9903 3.1369 10.3927 
下载: 导出CSV
表 2 四颗脉冲星的归一化权重
Table 2. Normalized weights of the four pulsars
PSR J0437-4715 J1713+0747 J1744-1134 J1909-3744 RMS/μs 0.215 0.457 0.653 0.191 $w_i$ 0.385 0.085 0.042 0.488
下载: 导出CSV
-
[1] Allan D W 1987 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 34 647
Google Scholar
[2] Panfilo G, Arias E F 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 140
[3] Kaplan G H 2006 arXiv: 0602086[astro-ph]
[4] Guinot B 1988 Astron. Astrophys. 192 370
[5] Petit G 2003 Proceedings of the 35th Annual Precise Time and Time Interval Systems and Applications Meeting San Diego, California, December 2–4, 2003 p317
[6] Gao Z F, Wang N, Shan H, Li X D, Wang W 2017 Astrophys. J. 849 19
Google Scholar
[7] Gao Z F, Li X D, Wang N, Yuan J P, Wang P, Peng Q H, Du Y J 2016 Mon. Not. R. Astron. Soc. 456 55
Google Scholar
[8] Fu G Z, Xing C C, Wang N 2020 Eur. Phys. J. C 80 582
Google Scholar
[9] Wang H, Gao Z F, Jia H Y, Wang N, Li X 2020 Universe 6 63
Google Scholar
[10] Zhu C, Gao Z F, Li X D, Wang N, Yuan J P, Peng Q 2016 Mod. Phys. Lett. A 31 1650070
[11] Yan F Z, Gao Z F, Yang W S, Dong A J 2021 Astron. Nachr. 342 249
Google Scholar
[12] Gao Z F, Wang N, Peng Q H, Li X D, Du Y J 2013 Mod. Phys. Lett. A 28 1350138
[13] Gao Z F, Song D L, Li X, Shan H, Wang N 2019 Astron. Nachr. 340 241
Google Scholar
[14] Deng Z L, Gao Z F, Li X D, Shao Y 2020 Astrophys. J. 892 4
Google Scholar
[15] Deng Z L, Li X D, Gao Z F, Shao Y 2021 Astrophys. J. 909 174
Google Scholar
[16] Lorimer D R, Kramer M 1965 Handbook of Pulsar Astronomy (New York: Cambridge University Press) pp32–34
[17] Coles W, Hobbs G, Champion D J, Manchester R N, Verbiest J P W 2011 Mon. Not. R. Astron. Soc. 418 561
Google Scholar
[18] Hobbs G, Guo L, Caballero R N, Coles W, Lee K J, Manchester R N, Reardon D J, Matsakis D, Tong M L, Arzoumanian Z, Bailes M, Bassa C G, Bhat N D R, Brazier A, Burke-Spolaor S, Champion D J, Chatterjee S, Cognard I, Dai S, Desvignes G, Dolch T, Ferdman R D, Graikou E, Guillemot L, Janssen G H, Keith M J, Kerr M, Kramer M, Lam M T, Liu K, Lyne A, Lazio T J W, Lynch R, McKee J W, McLaughlin M A, Mingarelli C M F, Nice D J, Osłowski S, Pennucci T T, Perera B B P, Perrodin D, Possenti A, Russell C J, Sanidas S, Sesana A, Shaifullah G, Shannon R M, Simon J, Spiewak R, Stairs I H, Stappers B W, Swiggum J K, Taylor S R, Theureau G, Toomey L, van Haasteren R, Wang J B, Wang Y, Zhu X J 2020 Mon. Not. R. Astron. Soc. 491 5951
Google Scholar
[19] Gao F, Tong M L, Gao Y P, Yang T G, Zhao C S 2019 Res. Astron. Astrophys. 19 100
Google Scholar
[20] Petit G, Tavella P 1985 Astron. Astrophys. 308 290
[21] Hobbs G, Coles W, Manchester R N, Keith M J, Shannon R M, Chen D, Bailes M, Bhat N D R, Burke-Spolaor S, Champion D, Chaudhary A, Hotan A, Khoo J, Kocz J, Levin Y, Oslowski S, Preisig B, Ravi V, Reynolds J E, Sarkissian J, van Straten W, Verbiest J P W, Yardley D, You X P 2012 Mon. Not. R. Astron. Soc. 427 2780
Google Scholar
[22] 仲崇霞, 杨廷高 2009 天文学报 50 425
Google Scholar
Zhong C X, Yang T G 2009 Acta Astronom. Sin. 50 425
Google Scholar
[23] Yang T G, Tong M L, Gao Y P 2022 Res. Astron. Astrophys. 22 105012
Google Scholar
[24] BIPM Time Department https://webtai.bipm.org/ftp/pub/tai/data/[2022-10-07]
[25] Hobbs G 2013 Classical Quant. Grav. 30 224007
Google Scholar
[26] PPTA Data Release https://doi.org/10.4225/08/534CC21379C12[2022-10-08]
[27] Hobbs G B, Edwards R T, Manchester R N 2006 Mon. Not. R. Astron. Soc. 369 655
Google Scholar
[28] Manchester R N, Hobbs G, Bailes M, Coles W A, van Straten W, Keith M J, Shannon R M, Bhat N D R, Brown A, Burke-Spolaor S G, Champion D J, Chaudhary A, Edwards R T, Hampson G, Hotan A W, Jameson A, Jenet F A, Kesteven M J, Khoo J, Kocz J, Maciesiak K, Oslowski S, Ravi V, Reynolds J R, Sarkissian J M, Verbiest J P W, Wen Z L, Wilson W E, Yardley D, Yan W M, You X P 2012 Publ. Astron. Soc. Pac 30 17
[29] Wiener N, Mathematician C 1949 Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications (Massachusetts: MIT press) pp1043–1054
[30] Rodin A E 2008 Mon. Not. R. Astron. Soc. 387 1583
Google Scholar
[31] Noor M A 1993 J. Optim. Theory Appl. 79 197
Google Scholar
[32] Kopeikin S M 1999 Mon. Not. R. Astron. Soc. 305 563
Google Scholar
[33] 童明雷, 杨廷高, 赵成仕, 高玉平 2017 中国科学: 物理学 力学 天文学 47 099503
Google Scholar
Tong M L, Yang T G, Zhao C S, Gao Y P 2017 Sci. Sin-Phys. Mech. Astron. 47 099503
Google Scholar
[34] Zhao R M, Cui H 2015 Proceedings of the 14th International Symposium on Plasma Chemistry Sousse, Tunisia, December 18–20, 2015 p1
[35] Shan H, Yuan J P, Wang N, Wang Z 2022 Astrophys. J. 935 117
Google Scholar
[36] 王英红, 王冬霞, 杨洪升 2004 辽宁工学院学报 24 7
Wang Y H, Wang D X, Yang H S 2004 Journal of Liaoning Institute of Technology 24 7
[37] Cameron A D, Li D, Hobbs G, Zhang L, Miao C C, Wang J B, Yuan M, Wang S, Jacobs Corban G, Cruces M, Dai S, Feng Y, Han J, Kaczmarek J F, Niu J R, Pan Z C, Qian L, Tao Z Z, Wang P, Wang S Q, Xu H, Xu R X, Yue Y L, Zhang S B, Zhi Q J, Zhu W W, Champion D J, Kramer M, Zhou S Q, Qiu K P, Zhu M 2020 Mon. Not. R. Astron. Soc. 495 3515
Google Scholar
[38] Han J L, Wang C, Wang P F, Wang T, Zhou D J, Sun J H, Yan Y, Su W Q, Jing W C, Chen X, Gao X Y, Hou L G, Xu J, Lee K J, Wang N, Jiang P, Xu R X, Yan J, Gan H Q, Guan X, Huang W J, Jiang J C, Li H, Men Y P, Sun C, Wang B J, Wang H G, Wang S Q, Xie J T, Xu H, Yao R, You X P, Yu D J, Yuan J P, Yuen R, Zhang C F, Zhu Y 2021 Res. Astron. Astrophys. 21 107
Google Scholar
下载:
计量
- 文章访问数: 3373
- PDF下载量: 67
- 被引次数: 0
