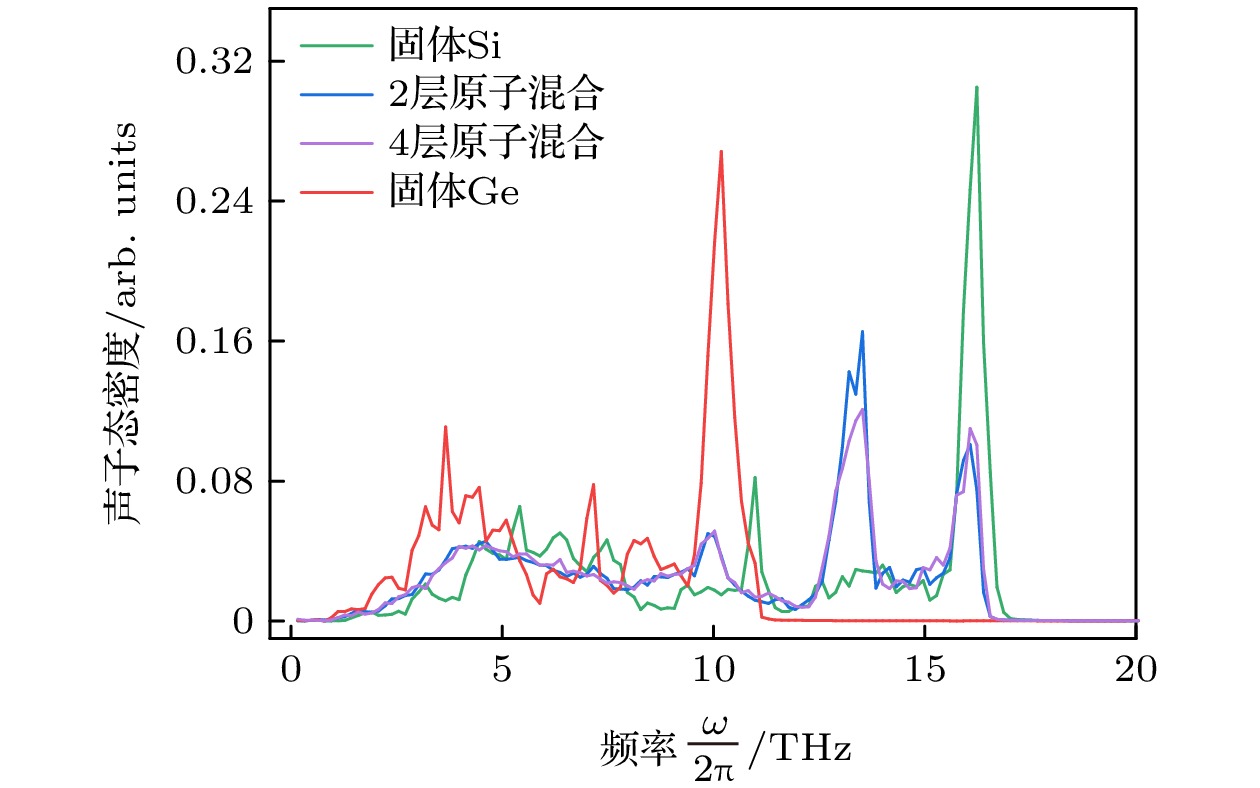
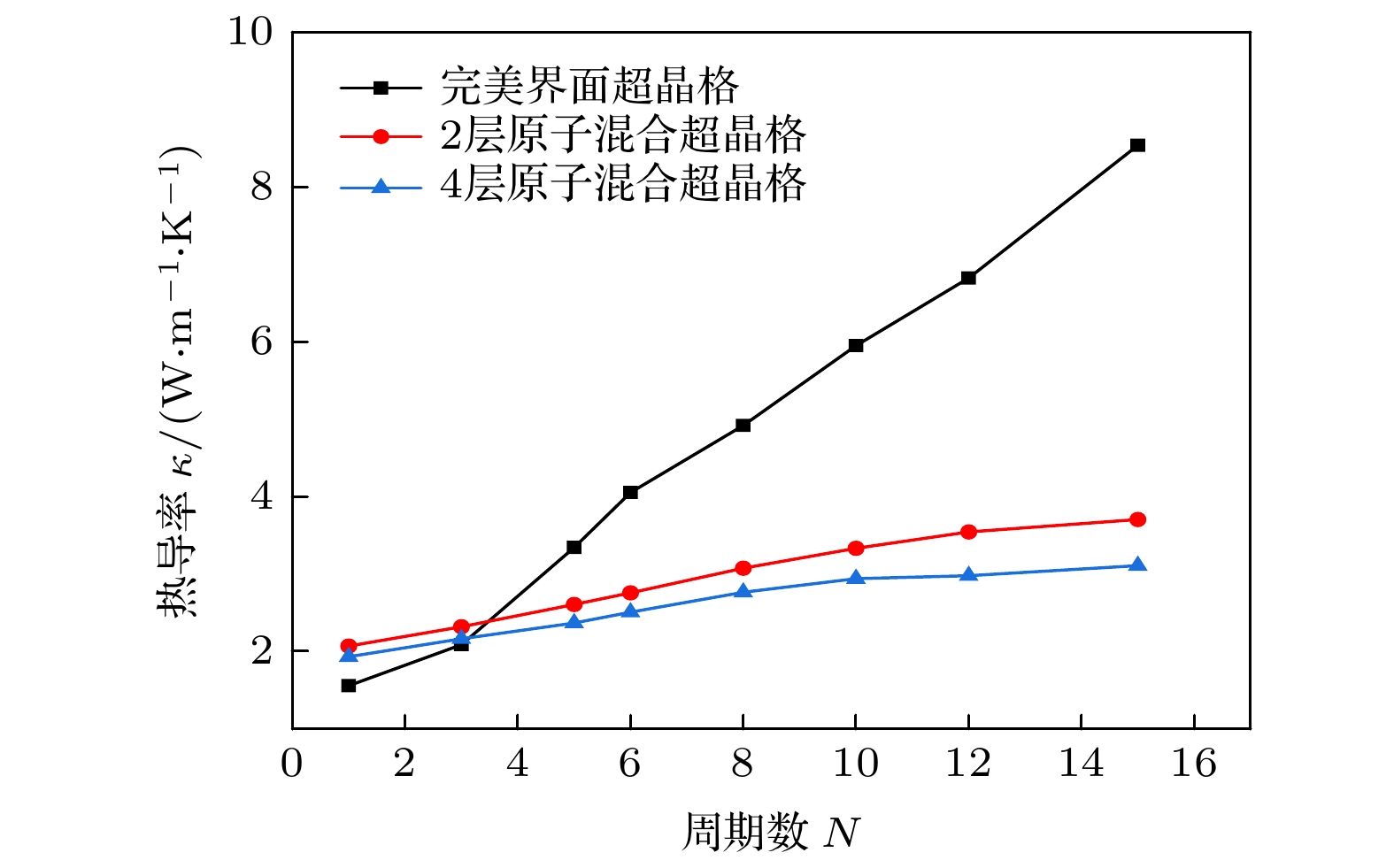
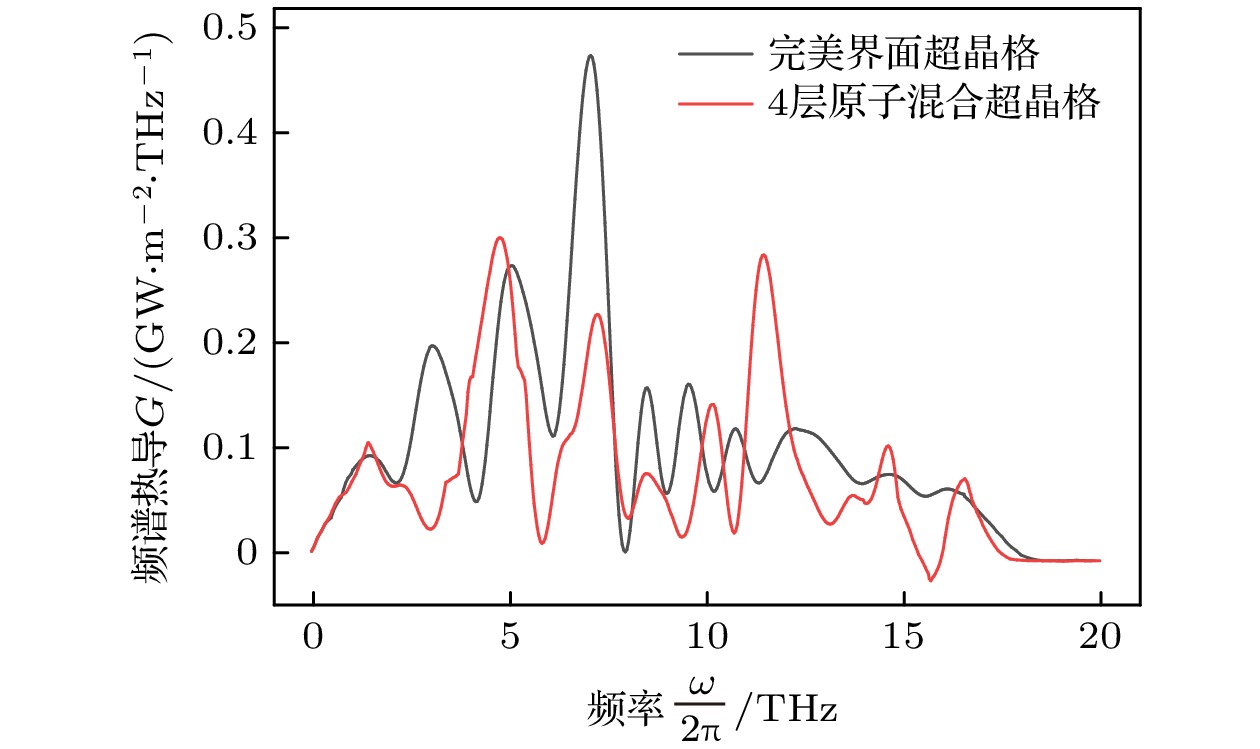
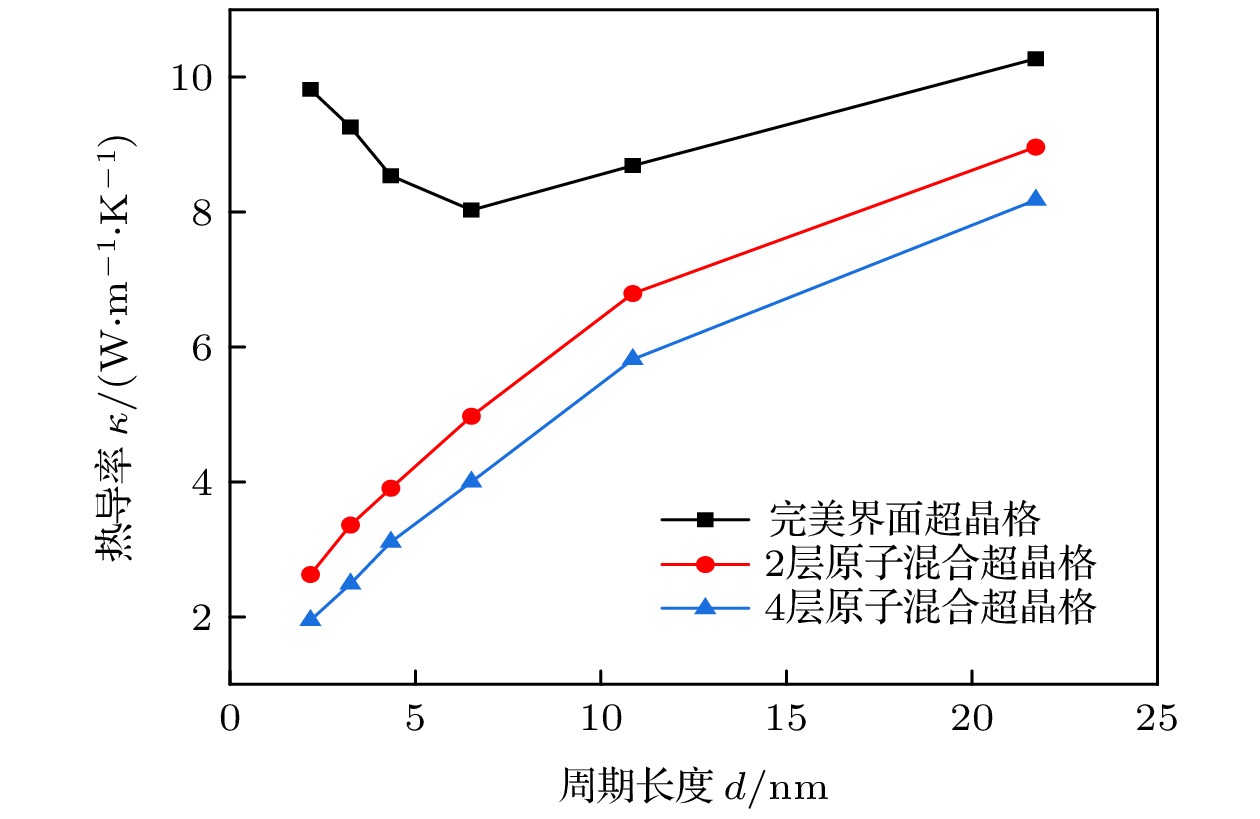
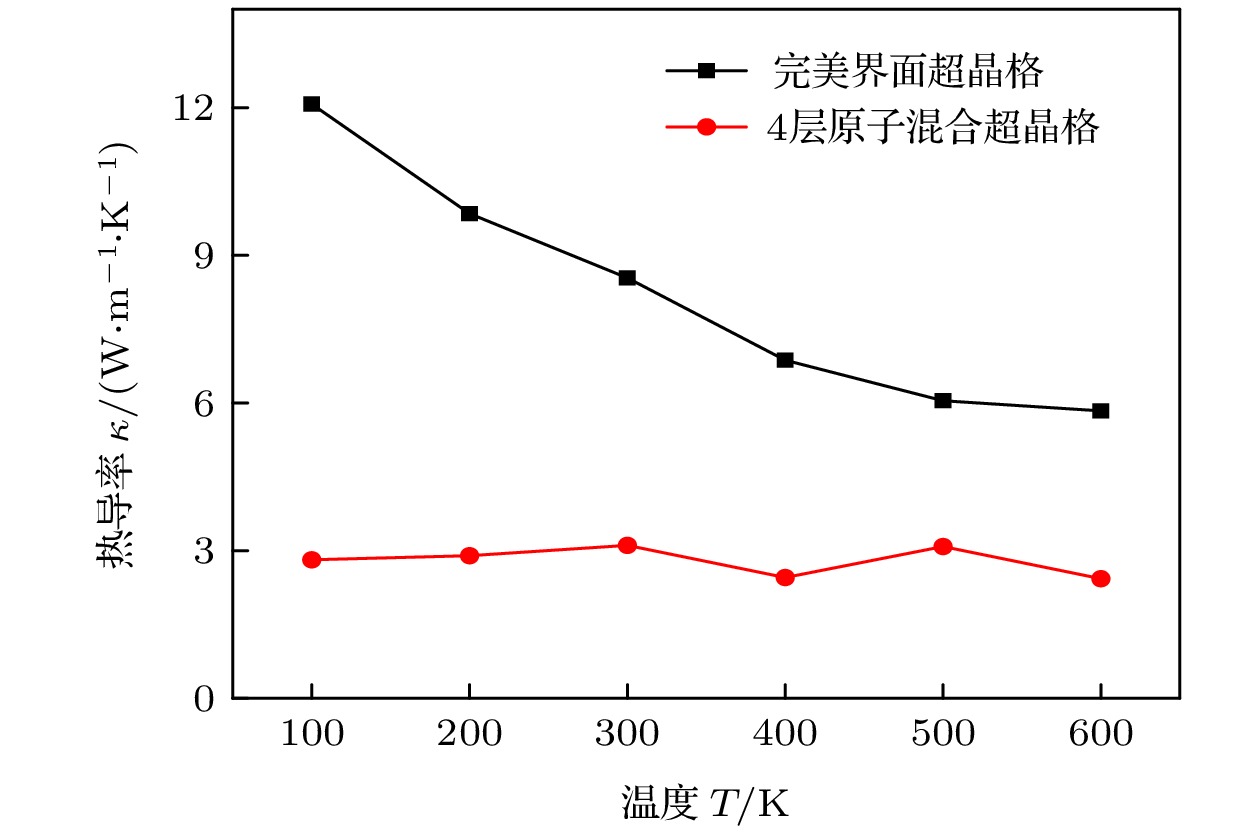
-
构造了界面具有原子混合的硅锗(Si/Ge)单界面和超晶格结构. 采用非平衡分子动力学模拟研究了界面原子混合对于单界面和超晶格结构热导率的影响, 重点研究了界面原子混合层数、环境温度、体系总长以及周期长度对不同晶格结构热导率的影响. 结果表明: 由于声子的“桥接”机制, 2层和4层界面原子混合能提高单一界面和少周期数的超晶格的热导率, 但是在多周期体系中, 具有原子混合时的热导率要低于完美界面时的热导率; 界面原子混合会破坏超晶格中声子的相干性输运, 一定程度引起热导率降低; 完美界面超晶格具有明显的温度效应, 而具有原子混合的超晶格热导率对温度的敏感性较低.The Si/Ge single interface and superlattice structure with atom mixing interfaces are constructed. The effects of interfacial atomic mixing on thermal conductivity of single interface and superlattice structures are studied by non-equilibrium molecular dynamics simulation. The effects of the number of atomic mixing layers, temperature, total length of the system and period length on the thermal conductivity for different lattice structures are studied. The results show that the mixing of two and four layers of atoms can improve the thermal conductivity of Si/Ge lattice with single interface and the few-period superlattice due to the “phonon bridging” mechanism. When the total length of the system is large, the thermal conductivity of the superlattice with atomic mixing interfaces decreases significantly compared with that of the perfect interface. The interfacial atom mixing will destroy the phonon coherent transport in the superlattice and reduce the thermal conductivity to some extent. The superlattce with perfect interface has obvious temperature effect, while the thermal conductivity of the superlattice with atomic mixing is less sensitive to temperature.
-
Keywords:
- single interface /
- superlattices /
- phonons /
- thermal conductivity
[1] Cahill D G, Ford W K, Goodson K E, Mahan G D, Majumdar A, Maris H J, Merlin R, Phillpot S R 2003 J. Appl. Phys. 93 793
Google Scholar
[2] 唐道胜, 曹炳阳 2021 工程热 42 1546
Tang D S, Cao B Y 2021 J. Eng. Thermophys. 42 1546
[3] Liang Z, Tsai H L 2012 Int. J. Heat Mass Transf. 55 2999
Google Scholar
[4] Chen W Y, Yang J K, Wei Z Y, Liu C H, Bi K D, Xu D Y, Li D Y, Chen Y F 2015 Phys. Rev. B 92 134113
Google Scholar
[5] Tian Z T, Esfarjani K, Chen G 2014 Phys. Rev. B 89 235307
Google Scholar
[6] Kechrakos D 1991 J. Phys. Condens. Matter 3 1443
Google Scholar
[7] Liang Z, Tsai H L 2011 J. Phys. Condens. Matter 23 495303
Google Scholar
[8] O'Brien P J, Shenogin S, Liu J X, Chow P K, Laurencin D, Mutin P H, Yamaguchi M, Keblinski P, Ramanath G 2013 Nat. Mater. 12 118
Google Scholar
[9] English T S, Duda J C, Smoyer J L, Jordan D A, Norris P M, Zhigilei L V 2012 Phys. Rev. B 85 035438
Google Scholar
[10] Shao C, Bao H 2015 Int. J. Heat Mass Transf. 85 33
Google Scholar
[11] Zhou Y G, Zhang X L, Hu M 2016 Nanoscale 8 1994
Google Scholar
[12] Stevens R J, Zhigilei L V, Norris P M 2007 Int. J. Heat Mass Transf. 50 3977
Google Scholar
[13] Tian Z T, Esfarjani K, Chen G 2012 Phys. Rev. B 86 235304
Google Scholar
[14] Jia L, Ju S H, Liang X G, Zhang X 2016 Mater. Res. Express 3 095024
Google Scholar
[15] Merabia S, Termentzidis K 2014 Phys. Rev. B 89 054309
Google Scholar
[16] Ravichandran J, Yadav A K, Cheaito R, Rossen P B, Soukiassian A, Suresha S J, Duda J C, Foley B M, Lee C H, Zhu Y, Lichtenberger A W, Moore J E, Muller D A, Schlom D G, Hopkins P E, Majumdar A, Ramesh R, Zurbuchen M A 2014 Nat. Mater. 13 168
Google Scholar
[17] Luckyanova M N, Mendoza J, Lu H, Song B, Huang S, Zhou J, Li M, Dong Y, Zhou H, Garlow J, Wu L, Kirby B J, Grutter A J, Puretzky A A, Zhu Y, Dresselhaus M S, Gossard A, Chen G 2018 Sci. Adv. 4 eaat9460
Google Scholar
[18] Chakraborty P, Chiu I A, Ma T F, Wang Y 2021 Nanotechnology 32 065401
Google Scholar
[19] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[20] 臧毅, 马登科, 杨诺 2017 工程热 38 2686
Zang Y, Ma D K, Yang N 2017 J. Eng. Thermophys. 38 2686
[21] Qu X L, Gu J J 2020 RSC Adv. 10 1243
Google Scholar
[22] Liang T, Zhou M, Zhang P, Yuan P, Yang D G 2020 Int. J. Heat Mass Transf. 151 119395
Google Scholar
[23] Chen J, Zhang G, Li B W 2010 Nano Lett. 10 3978
Google Scholar
[24] Wang Y, Vallabhaneni A, Hu J N, Qiu B, Chen Y P, Ruan X L 2014 Nano Lett. 14 592
Google Scholar
[25] Zhang Z W, Chen Y P, Xie Y E, Zhang S B 2016 Appl. Therm. Eng. 102 1075
Google Scholar
[26] Bodapati A, Schelling P K, Phillpot S R, Keblinski P 2006 Phys. Rev. B 74 245207
Google Scholar
[27] Sun Y D, Zhou Y G, Han J, Hu M, Xu B, Liu W 2020 J. Appl. Phys. 127 045106
Google Scholar
[28] Sääskilahti K, Oksanen J, Tulkki J, Volz S 2014 Phys. Rev. B 90 134312
Google Scholar
[29] Ma Y L, Zhang Z W, Chen J G, Sääskilahti K, Volz S, Chen J 2018 Carbon 135 263
Google Scholar
[30] Liu Y G, Bian Y Q, Chernatynskiy A, Han Z H 2019 Int. J. Heat Mass Transf. 145 118791
Google Scholar
[31] 刘英光, 郝将帅, 任国梁, 张静文 2021 70 073101
Google Scholar
Liu Y G, Hao J S, Ren G L, Zhang J W 2021 Acta Phys. Sin. 70 073101
Google Scholar
[32] 惠治鑫, 贺鹏飞, 戴瑛, 吴艾辉 2014 63 074401
Google Scholar
Hui Z X, He P F, Dai Y, Wu A H 2014 Acta Phys. Sin. 63 074401
Google Scholar
-
图 1 不同界面形式的Si/Ge原子模型结构示意图 (a)完美界面晶格结构; (b)界面具有原子混合晶格结构; (c)完美界面超晶格; (d)具有n层原子混合的超晶格
Fig. 1. Schematic diagram of Si/Ge atomic structure with different interface: (a) Single perfect interface; (b) single atomic mixing interface; (c) perfect superlattice; (d) superlattice with n-layer atomic mixing.
图 2 非平衡分子动力学模拟计算热性质示意图
Fig. 2. Schematic diagram of thermal properties calculated by non-equilibrium molecular dynamics simulation.
图 3 在环境温度为300 K时, Si/Ge晶格沿x轴向的温度分布
Fig. 3. Temperature profile in the x -direction of the Si/Ge lattice with ambient temperature is 300 K.
图 4 界面热导与原子混合层数的关系
Fig. 4. Thermal conductance as a function of the number of atomic mixing layers.
图 5 不同界面形式Si/Ge晶格的声子态密度
Fig. 5. Phonon density of states as a function of frequency for different Si/Ge interface forms.
图 6 超晶格热导率随周期数的变化
Fig. 6. Thermal conductivity of superlattices as a function of number of periods.
图 7 完美界面与4层原子混合界面的超晶格声子态密度
Fig. 7. Phonon density of states of superlattices with perfect interfaces and 4-layer atomic mixing.
图 8 完美界面和4层原子混合的超晶格的频谱热导
Fig. 8. Spectral thermal conductance of superlattices with perfect interfaces and 4-layer atomic mixing.
图 9 完美界面与4层原子混合的超晶格的声子参与率
Fig. 9. Phonon participation ratio of superlattices with perfect interfaces and 4-layer atomic mixing.
图 10 超晶格热导率与周期长度的关系
Fig. 10. Thermal conductivity of superlattices as a function of period length.
图 11 超晶格热导率随环境温度的变化
Fig. 11. Thermal conductivity of superlattices as a function of ambient temperature.
-
[1] Cahill D G, Ford W K, Goodson K E, Mahan G D, Majumdar A, Maris H J, Merlin R, Phillpot S R 2003 J. Appl. Phys. 93 793
Google Scholar
[2] 唐道胜, 曹炳阳 2021 工程热 42 1546
Tang D S, Cao B Y 2021 J. Eng. Thermophys. 42 1546
[3] Liang Z, Tsai H L 2012 Int. J. Heat Mass Transf. 55 2999
Google Scholar
[4] Chen W Y, Yang J K, Wei Z Y, Liu C H, Bi K D, Xu D Y, Li D Y, Chen Y F 2015 Phys. Rev. B 92 134113
Google Scholar
[5] Tian Z T, Esfarjani K, Chen G 2014 Phys. Rev. B 89 235307
Google Scholar
[6] Kechrakos D 1991 J. Phys. Condens. Matter 3 1443
Google Scholar
[7] Liang Z, Tsai H L 2011 J. Phys. Condens. Matter 23 495303
Google Scholar
[8] O'Brien P J, Shenogin S, Liu J X, Chow P K, Laurencin D, Mutin P H, Yamaguchi M, Keblinski P, Ramanath G 2013 Nat. Mater. 12 118
Google Scholar
[9] English T S, Duda J C, Smoyer J L, Jordan D A, Norris P M, Zhigilei L V 2012 Phys. Rev. B 85 035438
Google Scholar
[10] Shao C, Bao H 2015 Int. J. Heat Mass Transf. 85 33
Google Scholar
[11] Zhou Y G, Zhang X L, Hu M 2016 Nanoscale 8 1994
Google Scholar
[12] Stevens R J, Zhigilei L V, Norris P M 2007 Int. J. Heat Mass Transf. 50 3977
Google Scholar
[13] Tian Z T, Esfarjani K, Chen G 2012 Phys. Rev. B 86 235304
Google Scholar
[14] Jia L, Ju S H, Liang X G, Zhang X 2016 Mater. Res. Express 3 095024
Google Scholar
[15] Merabia S, Termentzidis K 2014 Phys. Rev. B 89 054309
Google Scholar
[16] Ravichandran J, Yadav A K, Cheaito R, Rossen P B, Soukiassian A, Suresha S J, Duda J C, Foley B M, Lee C H, Zhu Y, Lichtenberger A W, Moore J E, Muller D A, Schlom D G, Hopkins P E, Majumdar A, Ramesh R, Zurbuchen M A 2014 Nat. Mater. 13 168
Google Scholar
[17] Luckyanova M N, Mendoza J, Lu H, Song B, Huang S, Zhou J, Li M, Dong Y, Zhou H, Garlow J, Wu L, Kirby B J, Grutter A J, Puretzky A A, Zhu Y, Dresselhaus M S, Gossard A, Chen G 2018 Sci. Adv. 4 eaat9460
Google Scholar
[18] Chakraborty P, Chiu I A, Ma T F, Wang Y 2021 Nanotechnology 32 065401
Google Scholar
[19] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[20] 臧毅, 马登科, 杨诺 2017 工程热 38 2686
Zang Y, Ma D K, Yang N 2017 J. Eng. Thermophys. 38 2686
[21] Qu X L, Gu J J 2020 RSC Adv. 10 1243
Google Scholar
[22] Liang T, Zhou M, Zhang P, Yuan P, Yang D G 2020 Int. J. Heat Mass Transf. 151 119395
Google Scholar
[23] Chen J, Zhang G, Li B W 2010 Nano Lett. 10 3978
Google Scholar
[24] Wang Y, Vallabhaneni A, Hu J N, Qiu B, Chen Y P, Ruan X L 2014 Nano Lett. 14 592
Google Scholar
[25] Zhang Z W, Chen Y P, Xie Y E, Zhang S B 2016 Appl. Therm. Eng. 102 1075
Google Scholar
[26] Bodapati A, Schelling P K, Phillpot S R, Keblinski P 2006 Phys. Rev. B 74 245207
Google Scholar
[27] Sun Y D, Zhou Y G, Han J, Hu M, Xu B, Liu W 2020 J. Appl. Phys. 127 045106
Google Scholar
[28] Sääskilahti K, Oksanen J, Tulkki J, Volz S 2014 Phys. Rev. B 90 134312
Google Scholar
[29] Ma Y L, Zhang Z W, Chen J G, Sääskilahti K, Volz S, Chen J 2018 Carbon 135 263
Google Scholar
[30] Liu Y G, Bian Y Q, Chernatynskiy A, Han Z H 2019 Int. J. Heat Mass Transf. 145 118791
Google Scholar
[31] 刘英光, 郝将帅, 任国梁, 张静文 2021 70 073101
Google Scholar
Liu Y G, Hao J S, Ren G L, Zhang J W 2021 Acta Phys. Sin. 70 073101
Google Scholar
[32] 惠治鑫, 贺鹏飞, 戴瑛, 吴艾辉 2014 63 074401
Google Scholar
Hui Z X, He P F, Dai Y, Wu A H 2014 Acta Phys. Sin. 63 074401
Google Scholar
下载:
计量
- 文章访问数: 4468
- PDF下载量: 84
- 被引次数: 0
