-
基于全球地表气温资料, 分别构建了El Niño和La Niña事件对应的全球气温关联网络, 并分析网络结构特征的差异, 探究可能的成因. 结果表明, 与La Niña事件气温网络(简称La Niña网络)相比, El Niño事件气温网络(简称El Niño网络)中格点温度序列间的相关性减弱, 气温网络的连通度显著降低, 连通性下降, 在热带和南温带区域连通性变化尤为显著. 赤道东太平洋、赤道西太平洋、赤道印度洋和赤道大西洋的网络连通度相对较大, 在El Niño网络中的减少异常明显, 是导致两类网络结构特征差异性的4块关键区域. 在此基础上初步探讨了两类网络特征差异的原因, 即随着Niño3.4区域的海温升高, 赤道东太平洋、赤道印度洋等区域海温升高, 对外长波辐射加强, 对流活动增加, 低纬度与中纬度区域的相互作用增强, 南北温带气温变化的方差加大, 造成关键区格点气温序列与全球其他地区的相关性减弱, 全球格点气温网络连通性下降.Based on the global surface temperature data, the global temperature correlation networks corresponding to El Niño and La Niña events are constructed respectively, and the differences in their effects on the network topological structure properties are analyzed. The results show that compared with the La Niña temperature network, the correlation between grid temperature series in El Niño temperature network is weakened, and the connectivity of the network is significantly reduced, especially in the tropical region and the southern temperate region. The network connectivity degree of equatorial eastern Pacific, equatorial western Pacific, equatorial Indian Ocean and equatorial Atlantic Ocean are relatively large, and the decrease in El Niño network is notable. They are also the four key regions leading to the differences of the structural characteristics of the two types of network. On this basis, the reason for the difference between the two types of network characteristics is preliminarily discussed. With the increase of SST in Niño3.4 region, the SST in equatorial eastern Pacific, equatorial Indian Ocean and other areas rise, which strengthenes outgoing long wave radiation and convection activities, and the interaction between low latitude and mid-latitude areas, and the variance of air temperature changes in the north and south temperate regions increase. As a result, the correlation between the temperature series of the four key regions and the rest of the world is weakened, therefore the connectivity of the global grid temperature network is reduced.
-
Keywords:
- complex network of climate system /
- ENSO /
- nonlinear dynamics /
- network structure
[1] Timmermann A, An S I, Kug J S, Jin F F, Cai W J, Capotondi A, Cobb K M, Lengaigne M, McPhaden M J, Stuecker M F, Stein K, Wittenberg A T, Yun K S, Bayr T, Chen H C, Chikamoto Y, Dewitte B, Dommenget D, Grothe P, Guilyardi E, Ham Y G, Hayashi M, Ineson S, Kang D Y, Kim S Y, Kim W M, Lee J Y, Li T, Luo J J, McGregor S, Planton Y, Power S, Rashid H, Ren H L, Santoso A, Takahashi K, Todd A, Wang G, Wang G, Xie R, Yang W H, Yeh S W, Yoon J H, Zeller E, Zhang X B 2018 Nature 559 535
Google Scholar
[2] Michael J M, Stephen E Z, Michael H G 2006 Science 314 1740
Google Scholar
[3] Jia X, Lin H, Derome J 2009 Clim. Dyn. 32 495
Google Scholar
[4] Xie S P 1998 J. Clim. 11 189
[5] Huang R, Zhang R, Yan B 2001 Sci. China, Ser. D Earth Sci. 44 1089
Google Scholar
[6] Wang L, Chen W, Huang R 2008 Geophys. Res. Lett. 35 L20702
Google Scholar
[7] Lian Y, Shen B, Li S, Zhao B, Gao Z, Liu G, Liu P, Cao L 2013 Adv. Atmos. Sci. 30 193
Google Scholar
[8] Li J P, Sun C, Ding R Q 2018 Decadal Coupled Ocean–Atmosphere Interaction in North Atlantic and Global Warming Hiatus//Beer T, Li J P, Alverson K Global Change and Future Earth: The Geoscience Perspective (Cambridge: Cambridge University Press) pp131–143
[9] Wang G L, Tsonis A A 2009 Chin. Phys. B 18 5091
Google Scholar
[10] Boers N, Goswami B, Rheinwalt A, Bookhagen B, Hoskins B, Kurths J 2019 Nature 566 373
Google Scholar
[11] Fang J Q, Bi Q, Li Y 2007 Front. Phys. China 2 109
Google Scholar
[12] Nocke T, Buschmann S, Donges J F, Marwan N, Schulz H J, Tominski C 2015 Nonlinear Processes Geophys. 22 545
Google Scholar
[13] Fu Z T, Li Q I, Yuan N M, Yao Z H 2014 Commun. Nonlinear Sci. Numer. Simul. 19 83
Google Scholar
[14] Fu Z T, Shi L, Xie F H, Piao L 2016 Physica A 449 390
Google Scholar
[15] 李建平, 丑纪范 2003 大气科学 27 653
Google Scholar
Li J P, Chou J F 2003 Chin. J. Atmos. Sci. 27 653
Google Scholar
[16] Yuan N M, Lu Z H 2019 Nat. Clim. Change 10 13
[17] Tsonis A A, Roebber P J 2004 Physica A 333 497
Google Scholar
[18] Tsonis A A, Swanson K L 2008 Phys. Rev. Lett. 100 228502
Google Scholar
[19] Gong Z Q, Wang X J, Zhi R, Feng A X 2011 Chin. Phys. B 20 079201
Google Scholar
[20] 龚志强, 周磊, 支蓉, 封国林 2008 57 5351
Google Scholar
Gong Z Q, Zhou L, Zhi R, Feng G L 2008 Acta Phys. Sin. 57 5351
Google Scholar
[21] 龚志强 2009 博士学位论文 (兰州: 兰州大学)
Gong Z Q 2009 Ph. D. Dissertation (Lanzhou: Lanzhou University) (in Chinese)
[22] Ludescher J, Gozolchiani A, Bogachev M I, Bunde A, Havlin S, Schellnhuber H J 2014 Proc. Natl. Acad. Sci. 111 2064
[23] Ludescher Josef A G, Mikhail I B, Armin B, Shlomo H, Hans J S 2013 Proc. Natl. Acad. Sci. U.S.A. 110 11742
Google Scholar
[24] Yamasaki K, Gozolchiani A, Havlin S 2008 Phys. Rev. Lett. 100 228501
Google Scholar
[25] Radebach A, Donner R V, Runge J, Donges J F, Kurths J 2013 Phys. Rev. E 88 052807
Google Scholar
[26] Wiedermann M, Radebach A, Donges J F, Kurths J, Donner R V 2016 Geophys. Res. Lett. 43 7176
Google Scholar
[27] Lu Z H, Yuan N M, Chen L, Gong Z Q 2020 Geophys. Res. Lett. 47 e2019GL086533
[28] Lu Z H, Yuan N M, Fu Z T 2016 Sci. Rep. 6 1
Google Scholar
[29] Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K C, Ropelewski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D 1996 Bull. Am. Meteorol. Soc. 77 437
[30] Bollabas B 1985 Random Graphs (London: Academic Press) p20
[31] Tsonis A A, Swanson K L, Roebber P J 2006 Bull. Am. Meteorol. Soc. 87 585
Google Scholar
[32] Robusto C C 1957 Am. Math. Mon. 64 38
Google Scholar
[33] Albert R, Barabási A L 2002 Rev. Mod. Phys. 74 47
Google Scholar
-
图 1 不同ENSO相位下格点气温序列相关系数概率分布, 其中shuffled表示对格点气温序列作了随机化处理
Fig. 1. Probability distribution of correlation coefficient of grid temperature series under different ENSO phases, where shuffle represents randomization of grid temperature.
图 2 网络特征量空间分布 (a1), (a2)连通度; (b1), (b2)集聚系数; (c1), (c2)特征路径长度
Fig. 2. Spatial distribution of network characteristic quantity: (a1), (a2) Connectivity degree; (b1), (b2) agglomeration coefficient; (c1), (c2) characteristic path length.
图 3 不同区域网路特征量的概率分布 (a1)−(a4)连通度; (b1)−(b4)连通距离; (c1)−(c4)集聚系数; (d1)−(d4)最短路径长度. 由上到下4行依次对应全球网络、北温带网络、热带网络和南温带网络
Fig. 3. Probability distribution of (a1)−(a4) connectivity degree, (b1)−(b4) connectivity distance, (c1)−(c4) agglomeration coefficient, and (d1)−(d4) shortest path length of different regional network characteristic quantities. From top to bottom, four rows correspond to the global network, the northern temperate network, the tropical network, and the southern temperate network.
图 4 大洋关键区-全球气温关联网络连通度的空间分布图 (a1), (a2)大西洋关键区与全球相关; (b1), (b2)印度洋关键区与全球相关; (c1), (c2)赤道西太平洋关键区与全球相关; (d1), (d2)赤道东太平洋关键区与全球相关
Fig. 4. Spatial distribution of the connectivity between key regions of the ocean and global temperature network: (a1), (a2) Atlantic Ocean key region relevant to global; (b1), (b2) Indian Ocean key region relevant to global; (c1), (c2) equatorial western Pacific key region relevant to global; (d1), (d2) equatorial eastern Pacific key region relevant to global.
图 5 大洋关键区-全球气温关联网络连通性的概率分布图 (a1)−(a4)连通度; (b1)−(b4)链路距离. 其中(a1), (a2)为大西洋关键区与全球相关, (b1), (b2)为印度洋关键区与全球相关, (c1), (c2)为赤道西太平洋关键区与全球相关, (d1), (d2)为赤道东太平洋关键区与全球相关
Fig. 5. Probability distribution of the connectivity between key regions of ocean and global temperature correlation network: (a1)−(a4) Connectivity degree; (b1)−(b4) link distance. Panels (a1), (a2) correspond to the key region of the Atlantic Ocean relevant to global, panels (b1), (b2) correspond to the key region of the Indian Ocean relevant to global, panels (c1), (c2) correspond to the key region of the equatorial western Pacific relevant to global, panels (d1), (d2) correspond to the key region of the equatorial eastern Pacific relevant to global.
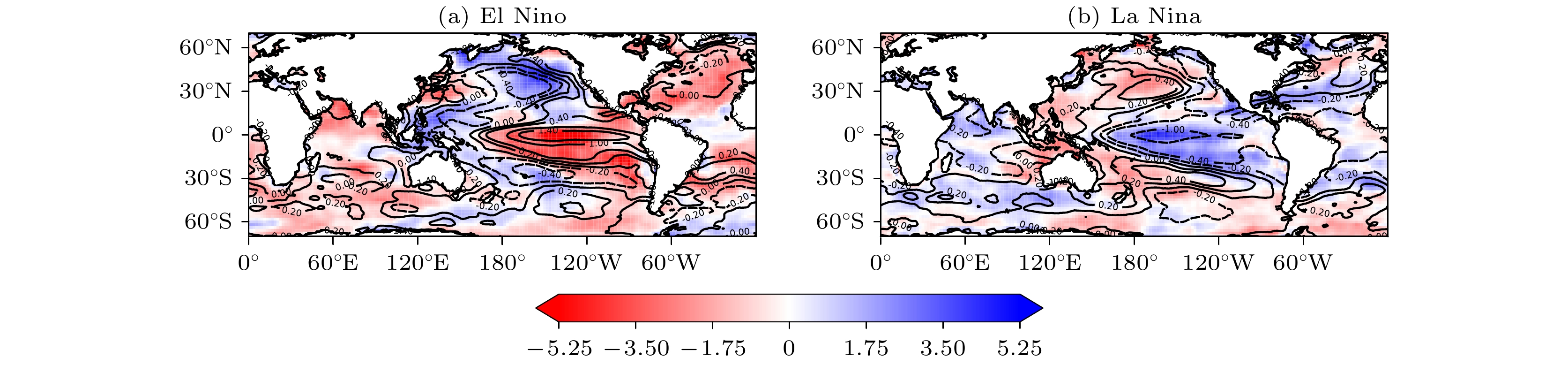
图 6 El Niño和La Niña事件对应的海温距平(等值线, 单位: ℃)和净长波辐射距平(填色部分, 单位:
$ {\mathrm{W}/\mathrm{m}}^{2} $ )空间分布图 (a) El Niño; (b) La NiñaFig. 6. Spatial distribution diagram of SST anomaly (isolines, unit: ℃) and net long-wave radiation anomaly (color filling, unit:
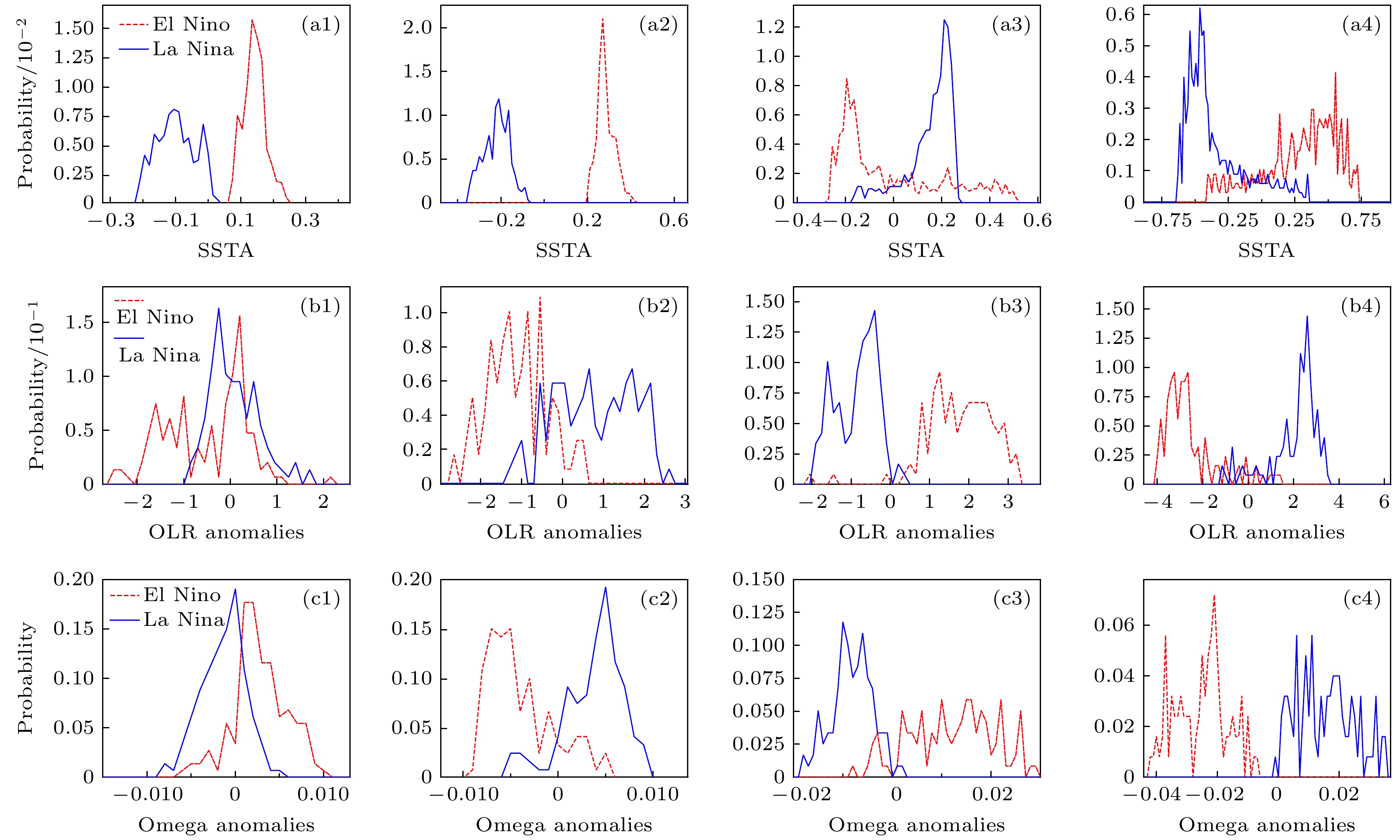
$ {\mathrm{W}/\mathrm{m}}^{2} $ ) corresponding to El Niño and La Niña events: (a) El Niño; (b) La Niña.
图 7 各关键区海温距平((a1)−(a4))、长波辐射距平((b1)−(b4))和垂直速度距平((c1)−(c4))的概率分布 (a1)−(c1)赤道大西洋; (a2)−(c2)赤道印度洋; (a3)−(c3)赤道西太平洋; (a4)−(c4)赤道东太平洋
Fig. 7. Probability distribution of SST anomaly ((a1)−(a4)), long-wave radiation anomaly ((b1)−(b4)) and vertical velocity anomaly ((c1)−(c4)) in each key area: (a1)−(c1) Equatorial Atlantic Ocean; (a2)−(c2) equatorial Indian Ocean; (a3)−(c3) equatorial western Pacific; (a4)−(c4) equatorial eastern Pacific.
图 8 排序后Niño 3.4区域冬半年的海温均值序列, 虚线内窗口宽度30 a, 滑动步长为1 a
Fig. 8. Sequence of mean SST of winter half year in Niño 3.4 region after sorting. The window width in the dashed line is 30 a, and the sliding step length is 1 a.
图 9 全球气温关联网络结构特征量平均值随Niño3.4区域海温升高变化特征 (a) 连通度; (b) 连通距离; (c)特征路径长度
Fig. 9. Variation characteristics of the mean value of structural characteristics of global temperature correlation network with the rise of SST in Niño3.4 region: (a) Connectivity degree; (b) connectivity distance; (c) characteristic path length.
图 10 大洋关键区域长波辐射、垂直速度场随Niño3.4指数升高的变化特征
Fig. 10. Variation characteristics of long wave radiation and vertical velocity fields in key regions of the ocean with Niño3.4 index increasing.
图 11 南温带(30°S−65°S)和北温带(30°N−65°N)平均气温方差随Niño3.4区域海温升高的变化图
Fig. 11. Variance of mean temperature in the south and north temperate regions (30°S−65°S, 30°N−65°N) with the increase of SST in Niño3.4.
表 1 连通度平均值与差异率
Table 1. Average connectivity and difference rate.
${ \widetilde {C}_{\mathrm{E}\mathrm{l}\;\mathrm{N}\mathrm{i}{\tilde {\rm{n} } }\mathrm{o} } }$ ${\widetilde {C}_{\mathrm{L}\mathrm{a}\;\mathrm{N}\mathrm{i}{\tilde {\rm{n} } }\mathrm{a} } }$ 差异率D 全球 0.035 0.055 55% 北温带 0.024 0.025 2% 热带 0.057 0.097 72% 南温带 0.020 0.033 63% 
下载: 导出CSV
表 2 各大洋关键区的划分范围
Table 2. Range of key regions in the oceans.
纬度 经度 赤道大西洋 5°N—10°S 40°W—10°E 赤道印度洋 10°N—5°S 60°E—100°E 赤道西太平洋 20°N—5°N 110°E—150°E 赤道东太平洋 5°N—5°S 170°W—120°W
下载: 导出CSV
-
[1] Timmermann A, An S I, Kug J S, Jin F F, Cai W J, Capotondi A, Cobb K M, Lengaigne M, McPhaden M J, Stuecker M F, Stein K, Wittenberg A T, Yun K S, Bayr T, Chen H C, Chikamoto Y, Dewitte B, Dommenget D, Grothe P, Guilyardi E, Ham Y G, Hayashi M, Ineson S, Kang D Y, Kim S Y, Kim W M, Lee J Y, Li T, Luo J J, McGregor S, Planton Y, Power S, Rashid H, Ren H L, Santoso A, Takahashi K, Todd A, Wang G, Wang G, Xie R, Yang W H, Yeh S W, Yoon J H, Zeller E, Zhang X B 2018 Nature 559 535
Google Scholar
[2] Michael J M, Stephen E Z, Michael H G 2006 Science 314 1740
Google Scholar
[3] Jia X, Lin H, Derome J 2009 Clim. Dyn. 32 495
Google Scholar
[4] Xie S P 1998 J. Clim. 11 189
[5] Huang R, Zhang R, Yan B 2001 Sci. China, Ser. D Earth Sci. 44 1089
Google Scholar
[6] Wang L, Chen W, Huang R 2008 Geophys. Res. Lett. 35 L20702
Google Scholar
[7] Lian Y, Shen B, Li S, Zhao B, Gao Z, Liu G, Liu P, Cao L 2013 Adv. Atmos. Sci. 30 193
Google Scholar
[8] Li J P, Sun C, Ding R Q 2018 Decadal Coupled Ocean–Atmosphere Interaction in North Atlantic and Global Warming Hiatus//Beer T, Li J P, Alverson K Global Change and Future Earth: The Geoscience Perspective (Cambridge: Cambridge University Press) pp131–143
[9] Wang G L, Tsonis A A 2009 Chin. Phys. B 18 5091
Google Scholar
[10] Boers N, Goswami B, Rheinwalt A, Bookhagen B, Hoskins B, Kurths J 2019 Nature 566 373
Google Scholar
[11] Fang J Q, Bi Q, Li Y 2007 Front. Phys. China 2 109
Google Scholar
[12] Nocke T, Buschmann S, Donges J F, Marwan N, Schulz H J, Tominski C 2015 Nonlinear Processes Geophys. 22 545
Google Scholar
[13] Fu Z T, Li Q I, Yuan N M, Yao Z H 2014 Commun. Nonlinear Sci. Numer. Simul. 19 83
Google Scholar
[14] Fu Z T, Shi L, Xie F H, Piao L 2016 Physica A 449 390
Google Scholar
[15] 李建平, 丑纪范 2003 大气科学 27 653
Google Scholar
Li J P, Chou J F 2003 Chin. J. Atmos. Sci. 27 653
Google Scholar
[16] Yuan N M, Lu Z H 2019 Nat. Clim. Change 10 13
[17] Tsonis A A, Roebber P J 2004 Physica A 333 497
Google Scholar
[18] Tsonis A A, Swanson K L 2008 Phys. Rev. Lett. 100 228502
Google Scholar
[19] Gong Z Q, Wang X J, Zhi R, Feng A X 2011 Chin. Phys. B 20 079201
Google Scholar
[20] 龚志强, 周磊, 支蓉, 封国林 2008 57 5351
Google Scholar
Gong Z Q, Zhou L, Zhi R, Feng G L 2008 Acta Phys. Sin. 57 5351
Google Scholar
[21] 龚志强 2009 博士学位论文 (兰州: 兰州大学)
Gong Z Q 2009 Ph. D. Dissertation (Lanzhou: Lanzhou University) (in Chinese)
[22] Ludescher J, Gozolchiani A, Bogachev M I, Bunde A, Havlin S, Schellnhuber H J 2014 Proc. Natl. Acad. Sci. 111 2064
[23] Ludescher Josef A G, Mikhail I B, Armin B, Shlomo H, Hans J S 2013 Proc. Natl. Acad. Sci. U.S.A. 110 11742
Google Scholar
[24] Yamasaki K, Gozolchiani A, Havlin S 2008 Phys. Rev. Lett. 100 228501
Google Scholar
[25] Radebach A, Donner R V, Runge J, Donges J F, Kurths J 2013 Phys. Rev. E 88 052807
Google Scholar
[26] Wiedermann M, Radebach A, Donges J F, Kurths J, Donner R V 2016 Geophys. Res. Lett. 43 7176
Google Scholar
[27] Lu Z H, Yuan N M, Chen L, Gong Z Q 2020 Geophys. Res. Lett. 47 e2019GL086533
[28] Lu Z H, Yuan N M, Fu Z T 2016 Sci. Rep. 6 1
Google Scholar
[29] Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K C, Ropelewski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D 1996 Bull. Am. Meteorol. Soc. 77 437
[30] Bollabas B 1985 Random Graphs (London: Academic Press) p20
[31] Tsonis A A, Swanson K L, Roebber P J 2006 Bull. Am. Meteorol. Soc. 87 585
Google Scholar
[32] Robusto C C 1957 Am. Math. Mon. 64 38
Google Scholar
[33] Albert R, Barabási A L 2002 Rev. Mod. Phys. 74 47
Google Scholar
下载:
计量
- 文章访问数: 4756
- PDF下载量: 74
- 被引次数: 0
