共轭线性对称性及其对<inline-formula><tex-math id="M1">\begin{document}$ {\mathcal{P}}{\mathcal{T}} $\end{document}</tex-math><alternatives><graphic xmlns:xlink="http://www.w3.org/1999/xlink" xlink:href="3-20191173_M1.jpg"/><graphic xmlns:xlink="http://www.w3.org/1999/xlink" xlink:href="3-20191173_M1.png"/></alternatives></inline-formula>-对称量子理论的应用

黄永峰; 曹怀信; 王文华

doi:10.7498/aps.69.20191173

摘要

传统量子系统的哈密顿是自伴算子, 哈密顿的自伴性不仅保证系统遵循酉演化和保持概率守恒, 而且也保证了它自身具有实的能量本征值, 这类系统称为自伴量子系统. 然而, 确实存在一些物理系统(如$ {\mathcal{P}}{\mathcal{T}} $-对称量子系统), 其哈密顿不是自伴的, 这类系统称为非自伴量子系统. 为了深入研究$ {\mathcal{P}}{\mathcal{T}} $-对称量子系统, 并考虑到算子$ {\mathcal{P}}{\mathcal{T}} $的共轭线性性, 首先讨论了共轭线性算子的一些性质, 包括它们的矩阵表示和谱结构等; 其次, 分别研究了具有共轭线性对称性和完整共轭线性对称性的线性算子, 通过它们的矩阵表示, 给出了共轭线性对称性和完整共轭线性对称性的等价刻画; 作为应用, 得到了关于$ {\mathcal{P}}{\mathcal{T}} $-对称及完整$ {\mathcal{P}}{\mathcal{T}} $-对称算子的一些有趣性质, 并通过一些具体例子, 说明了完整$ {\mathcal{P}}{\mathcal{T}} $-对称性对张量积运算不具有封闭性, 同时说明了完整$ {\mathcal{P}}{\mathcal{T}} $-对称性既不是哈密顿算子在某个正定内积下自伴的充分条件, 也不是必要条件.

关键词:

Abstract

The Hamiltonians of classical quantum systems are Hermitian (self-adjoint) operators. The self-adjointness of a Hamiltonian not only ensures that the system follows unitary evolution and preserves probability conservation, but also guarantee that the Hamiltonian has real energy eigenvalues. We call such systems Hermitian quantum systems. However, there exist indeed some physical systems whose Hamiltonians are not Hermitian, for instance, $ {\mathcal{P}}{\mathcal{T}} $-symmetry quantum systems. We refer to such systems as non-Hermitian quantum systems. To discuss in depth $ {\mathcal{P}}{\mathcal{T}} $-symmetry quantum systems, some properties of conjugate linear operators are discussed first in this paper due to the conjugate linearity of the operator $ {\mathcal{P}}{\mathcal{T}}, $ including their matrix represenations, spectral structures, etc. Second, the conjugate linear symmetry and unbroken conjugate linear symmetry are introduced for linear operators, and some equivalent characterizations of unbroken conjugate linear symmetry are obtained in terms of the matrix representations of the operators. As applications, $ {\mathcal{P}}{\mathcal{T}} $-symmetry and unbroken $ {\mathcal{P}}{\mathcal{T}} $-symmetry of Hamiltonians are discussed, showing that unbroken $ {\mathcal{P}}{\mathcal{T}} $-symmetry is not closed under taking tensor-product operation by some specific examples. Moreover, it is also illustrated that the unbroken $ {\mathcal{P}}{\mathcal{T}} $-symmetry is neither a sufficient condition nor a necessary condition for Hamiltonian to be Hermitian under a new positive definite inner product.

Keywords:

作者及机构信息

1.
陕西师范大学数学与信息科学学院, 西安　710119

2.
昌吉学院数学系, 昌吉　831100

3.
陕西师范大学民族教育学院, 西安　710119

通信作者: 曹怀信, caohx@snnu.edu.cn

基金项目: 国家自然科学基金(批准号: 11871318, 11771009, 11601300, 11571213)和中央高校基本科研业务费专项资金(批准号: GK201703093, GK201801011)资助的课题

Authors and contacts

1.
School of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710119, China

2.
School of Mathematics, Changji University, Changji 831100, China

3.
School of Ethnic Education, Shaanxi Normal University, Xi’an 710119, China

Corresponding author: Cao Huai-Xin, caohx@snnu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11371012, 11771009, 11601300, 11571213) and the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant Nos. GK201703093, GK201801011)

文章全文 : translate this paragraph

参考文献

[1]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[2]	Bender C M, Berry M V, Mandilara A 2002 J. Phys. A: Math. Theor. 35 L467 Google Scholar
[3]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401
[4]	Bender C M, Brandt S F, Chen J H, Wang Q H 2005 Phys. Rev. D 71 025014 Google Scholar
[5]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[6]	Bender C M, Klevansky S P 2009 Phys. Lett. 373 2670 Google Scholar
[7]	Bender C M, Gianfreda M 2013 J. Phys. A: Math. Theor. 46 275306 Google Scholar
[8]	Mostafazadeh A 2002 J. Math. Phys. 43 205
[9]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[10]	Mostafazadeh A 2002 J. Math. Phys. 43 3944 Google Scholar
[11]	Mostafazadeh A 2007 Phys. Rev. Lett. 99 130502 Google Scholar
[12]	Mostafazadeh A 2010 Int. J. Geom. Methods. M 7 1191 Google Scholar
[13]	Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403 Google Scholar
[14]	Zheng C, Hao L, Long G L 2013 Phil. Trans. R. Soc. A 371 20120053 Google Scholar
[15]	Rüter E C, Makris G K, Ganainy E R, Christodoulides N D, Segev M, Kip D 2010 Nat. Phys. 6 192 Google Scholar
[16]	Bender C M, Mannheim P D 2011 Phys. Rev. D 84 105038 Google Scholar
[17]	Kevrekidis P G 2014 Phys. Rev. A 89 010102 Google Scholar
[18]	Chen S L, Chen G Y, Chen Y N 2014 Phys. Rev. A 90 054301 Google Scholar
[19]	Lee C Y, Hsieh H M, Flammia T S, Lee K R 2014 Phys. Rev. Lett. 112 130404 Google Scholar
[20]	Tang J S, Wang Y T, Yu S, He D Y, Xu J S, Liu B H, Chen G, Sun Y N, Sun K, Han Y J, Li C F, Guo G C 2016 Nat. Photonics 10 642 Google Scholar
[21]	Mochizuki K, Kim D, Obuse H 2016 Phys. Rev. A 93 062116 Google Scholar
[22]	Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders C B, Xue P 2017 Nat. Phys. 13 1117 Google Scholar
[23]	Izaac A J, Wang B J, Abbott C P, Ma S X 2017 Phys. Rev. A 96 032305 Google Scholar
[24]	Smith J K, Mathur H 2010 Phys. Rev. A 82 042101 Google Scholar
[25]	Ashok D 2011 J. Phys. Conf. Ser. 287 012002 Google Scholar
[26]	Longhi S 2011 J. Phys. A: Math. Theor. 44 485302 Google Scholar
[27]	Cao H X, Guo Z H, Chen Z L 2013 Commun. Theor. Phys. 60 328 Google Scholar
[28]	Guo Z H, Cao H X, Lu L 2014 Sci. China: Phys. Mech. Astron. 57 1835
[29]	Deffner S, Saxena A 2015 Phys. Rev. Lett. 114 150601 Google Scholar
[30]	Croke S 2015 Phys. Rev. A 91 052113 Google Scholar
[31]	Brody D C 2016 J. Phys. A: Math. Theor. 49 10LT03 Google Scholar
[32]	Longhi S, Fisica D D 2017 Sci. Bull. 62 869 Google Scholar
[33]	Huang M Y, Kumar A, Wu J D 2018 Phys. Lett. A 382 2578 Google Scholar
[34]	Huang M Y, Lee K R, Wu J D 2018 J. Phys. A: Math. Theor. 51 414004 Google Scholar
[35]	Ramy E G, Konstantinos G M, Mercedeh K, Ziad H M, Stefan R, Demetrios N C 2018 Nat. Phys. 14 11 Google Scholar
[36]	Zhu W W, Fang X S, Li D T, Sun Y, Li Y, Jing Y, Chen H 2018 Phys. Rev. Lett. 121 124501 Google Scholar
[37]	黄永峰, 曹怀信, 王文华 2019 数学学报 62 469 Google Scholar Huang Y F, Cao H X, Wang W H 2019 Acta. Math. Sin. 62 469 Google Scholar
[38]	Huang M Y, Lee R K, Zhang L J, Fei S M, Wu J D 2019 Phys. Rev. Lett. 123 080404 Google Scholar
[39]	Horn A R, Johnson R C 2013 Matrix Analysis (2nd Ed.) (Cambridge: Cambridge University Press) pp163–187

施引文献

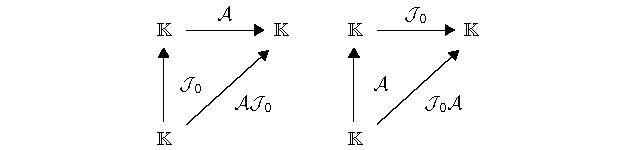
图 1 共轭线性算子$ {\mathcal{A}} $与$ {\mathcal{T}}_0 $的复合算子$ {\mathcal{A}}{\mathcal{T}}_0 $(左)与$ {\mathcal{T}}_0{\mathcal{A}} $(右)都是线性算子, 且满足关系 $ {\mathcal{A}}=({\mathcal{A}}{\mathcal{T}}_0){\mathcal{T}}_0= $${\mathcal{T}}_0({\mathcal{T}}_0{\mathcal{A}}) $

Fig. 1. Composition operators $ {\mathcal{A}}{\mathcal{T}}_0 $ (left) and $ {\mathcal{T}}_0{\mathcal{A}} $ (right), composed of conjugate linear operators $ {\mathcal{A}} $ and $ {\mathcal{T}}_0 $, which are linear operators and satisfy $ {\mathcal{A}}=({\mathcal{A}}{\mathcal{T}}_0){\mathcal{T}}_0={\mathcal{T}}_0({\mathcal{T}}_0{\mathcal{A}}) $

下载: 全尺寸图片幻灯片

map

[1]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[2]	Bender C M, Berry M V, Mandilara A 2002 J. Phys. A: Math. Theor. 35 L467 Google Scholar
[3]	Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401
[4]	Bender C M, Brandt S F, Chen J H, Wang Q H 2005 Phys. Rev. D 71 025014 Google Scholar
[5]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[6]	Bender C M, Klevansky S P 2009 Phys. Lett. 373 2670 Google Scholar
[7]	Bender C M, Gianfreda M 2013 J. Phys. A: Math. Theor. 46 275306 Google Scholar
[8]	Mostafazadeh A 2002 J. Math. Phys. 43 205
[9]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[10]	Mostafazadeh A 2002 J. Math. Phys. 43 3944 Google Scholar
[11]	Mostafazadeh A 2007 Phys. Rev. Lett. 99 130502 Google Scholar
[12]	Mostafazadeh A 2010 Int. J. Geom. Methods. M 7 1191 Google Scholar
[13]	Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403 Google Scholar
[14]	Zheng C, Hao L, Long G L 2013 Phil. Trans. R. Soc. A 371 20120053 Google Scholar
[15]	Rüter E C, Makris G K, Ganainy E R, Christodoulides N D, Segev M, Kip D 2010 Nat. Phys. 6 192 Google Scholar
[16]	Bender C M, Mannheim P D 2011 Phys. Rev. D 84 105038 Google Scholar
[17]	Kevrekidis P G 2014 Phys. Rev. A 89 010102 Google Scholar
[18]	Chen S L, Chen G Y, Chen Y N 2014 Phys. Rev. A 90 054301 Google Scholar
[19]	Lee C Y, Hsieh H M, Flammia T S, Lee K R 2014 Phys. Rev. Lett. 112 130404 Google Scholar
[20]	Tang J S, Wang Y T, Yu S, He D Y, Xu J S, Liu B H, Chen G, Sun Y N, Sun K, Han Y J, Li C F, Guo G C 2016 Nat. Photonics 10 642 Google Scholar
[21]	Mochizuki K, Kim D, Obuse H 2016 Phys. Rev. A 93 062116 Google Scholar
[22]	Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders C B, Xue P 2017 Nat. Phys. 13 1117 Google Scholar
[23]	Izaac A J, Wang B J, Abbott C P, Ma S X 2017 Phys. Rev. A 96 032305 Google Scholar
[24]	Smith J K, Mathur H 2010 Phys. Rev. A 82 042101 Google Scholar
[25]	Ashok D 2011 J. Phys. Conf. Ser. 287 012002 Google Scholar
[26]	Longhi S 2011 J. Phys. A: Math. Theor. 44 485302 Google Scholar
[27]	Cao H X, Guo Z H, Chen Z L 2013 Commun. Theor. Phys. 60 328 Google Scholar
[28]	Guo Z H, Cao H X, Lu L 2014 Sci. China: Phys. Mech. Astron. 57 1835
[29]	Deffner S, Saxena A 2015 Phys. Rev. Lett. 114 150601 Google Scholar
[30]	Croke S 2015 Phys. Rev. A 91 052113 Google Scholar
[31]	Brody D C 2016 J. Phys. A: Math. Theor. 49 10LT03 Google Scholar
[32]	Longhi S, Fisica D D 2017 Sci. Bull. 62 869 Google Scholar
[33]	Huang M Y, Kumar A, Wu J D 2018 Phys. Lett. A 382 2578 Google Scholar
[34]	Huang M Y, Lee K R, Wu J D 2018 J. Phys. A: Math. Theor. 51 414004 Google Scholar
[35]	Ramy E G, Konstantinos G M, Mercedeh K, Ziad H M, Stefan R, Demetrios N C 2018 Nat. Phys. 14 11 Google Scholar
[36]	Zhu W W, Fang X S, Li D T, Sun Y, Li Y, Jing Y, Chen H 2018 Phys. Rev. Lett. 121 124501 Google Scholar
[37]	黄永峰, 曹怀信, 王文华 2019 数学学报 62 469 Google Scholar Huang Y F, Cao H X, Wang W H 2019 Acta. Math. Sin. 62 469 Google Scholar
[38]	Huang M Y, Lee R K, Zhang L J, Fei S M, Wu J D 2019 Phys. Rev. Lett. 123 080404 Google Scholar
[39]	Horn A R, Johnson R C 2013 Matrix Analysis (2nd Ed.) (Cambridge: Cambridge University Press) pp163–187

[1]	王菲菲, 方建会, 王英丽, 徐瑞莉. 离散变质量完整系统的Noether对称性与Mei对称性. , 2014, 63(17): 170202. doi: 10.7498/aps.63.170202
[2]	张斌, 方建会, 张克军. 变质量非完整系统的Lagrange对称性与守恒量. , 2012, 61(2): 021101. doi: 10.7498/aps.61.021101
[3]	李元成, 夏丽莉, 王小明, 刘晓巍. 完整系统Appell方程的Lie-Mei对称性与守恒量. , 2010, 59(6): 3639-3642. doi: 10.7498/aps.59.3639
[4]	张宏彬, 吕洪升, 顾书龙. 完整约束力学系统保Lie对称性差分格式. , 2010, 59(8): 5213-5218. doi: 10.7498/aps.59.5213
[5]	李元成, 王小明, 夏丽莉. 完整系统Nielsen方程的统一对称性与守恒量. , 2010, 59(5): 2935-2938. doi: 10.7498/aps.59.2935
[6]	董文山, 黄宝歆. 广义非完整力学系统的Lie对称性与Noether守恒量. , 2010, 59(1): 1-6. doi: 10.7498/aps.59.1
[7]	张毅, 葛伟宽. 非Chetaev型非完整系统的Lagrange对称性与守恒量. , 2009, 58(11): 7447-7451. doi: 10.7498/aps.58.7447
[8]	路凯, 方建会, 张明江, 王鹏. 相空间中离散完整系统的Noether对称性和Mei对称性. , 2009, 58(11): 7421-7425. doi: 10.7498/aps.58.7421
[9]	贾利群, 罗绍凯, 张耀宇. 非完整系统Nielsen方程的Mei对称性与Mei守恒量. , 2008, 57(4): 2006-2010. doi: 10.7498/aps.57.2006
[10]	葛伟宽. 一类完整系统的Mei对称性与守恒量. , 2008, 57(11): 6714-6717. doi: 10.7498/aps.57.6714
[11]	张毅. 事件空间中完整系统的Lie对称性与绝热不变量. , 2007, 56(6): 3054-3059. doi: 10.7498/aps.56.3054
[12]	郑世旺, 贾利群. 非完整系统Tzénoff方程的Mei对称性和守恒量. , 2007, 56(2): 661-665. doi: 10.7498/aps.56.661
[13]	楼智美. 一类多自由度线性耦合系统的对称性与守恒量研究. , 2007, 56(5): 2475-2478. doi: 10.7498/aps.56.2475
[14]	张毅. 单面完整约束系统的速度依赖对称性与Lutzky守恒量. , 2006, 55(5): 2109-2114. doi: 10.7498/aps.55.2109
[15]	方建会, 丁宁, 王鹏. 非完整力学系统的Noether-Lie对称性. , 2006, 55(8): 3817-3820. doi: 10.7498/aps.55.3817
[16]	顾书龙, 张宏彬. Emden方程的Mei对称性、Lie对称性和Noether对称性. , 2006, 55(11): 5594-5597. doi: 10.7498/aps.55.5594
[17]	李　红, 方建会. 变质量单面完整约束系统的Mei对称性. , 2004, 53(9): 2807-2810. doi: 10.7498/aps.53.2807
[18]	罗绍凯. Hamilton系统的Mei对称性、Noether对称性和Lie对称性. , 2003, 52(12): 2941-2944. doi: 10.7498/aps.52.2941
[19]	王正平, 滕冰, 杜晨林, 许心光, 傅琨, 许贵宝, 王继扬, 邵宗书. 低对称性非线性光学晶体BIBO的倍频性质. , 2003, 52(9): 2176-2184. doi: 10.7498/aps.52.2176
[20]	景辉, 时庆云. 变系数积分变换与Landau体系的非线性-超对称性方法研究. , 1999, 48(9): 1581-1586. doi: 10.7498/aps.48.1581

计量

文章访问数: 8882
PDF下载量: 88
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

共轭线性对称性及其对$ {\mathcal{P}}{\mathcal{T}} $-对称量子理论的应用