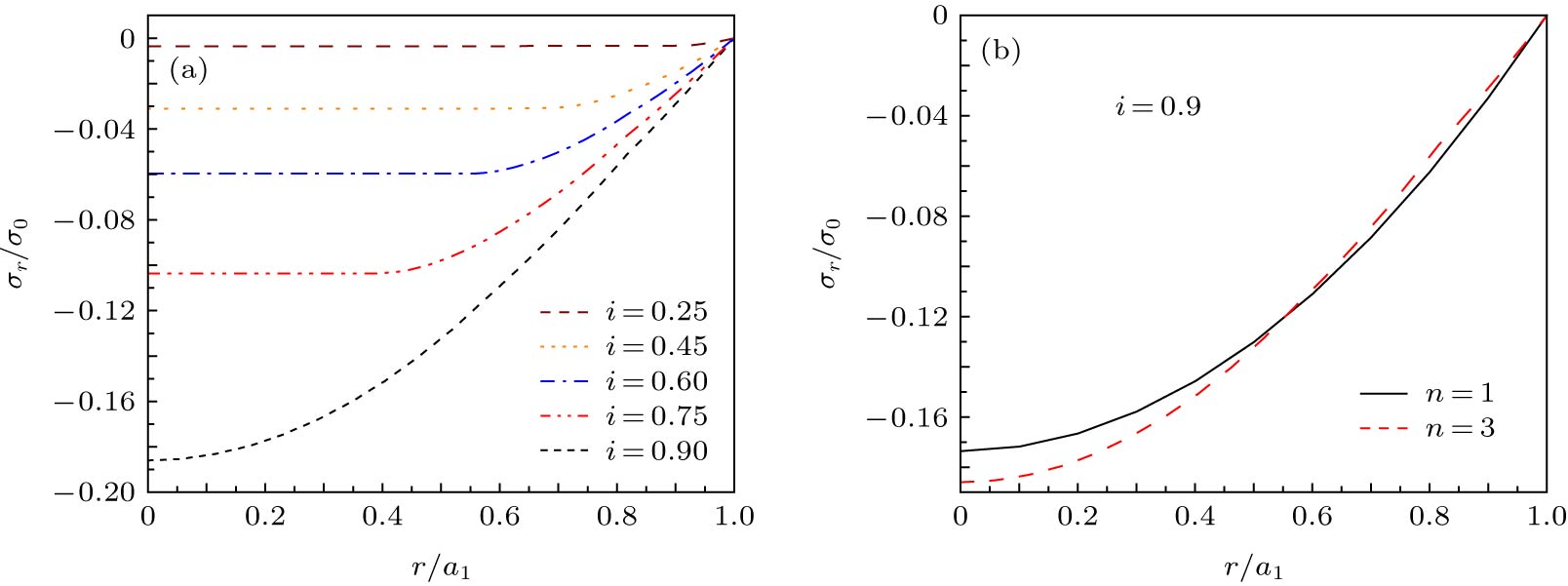
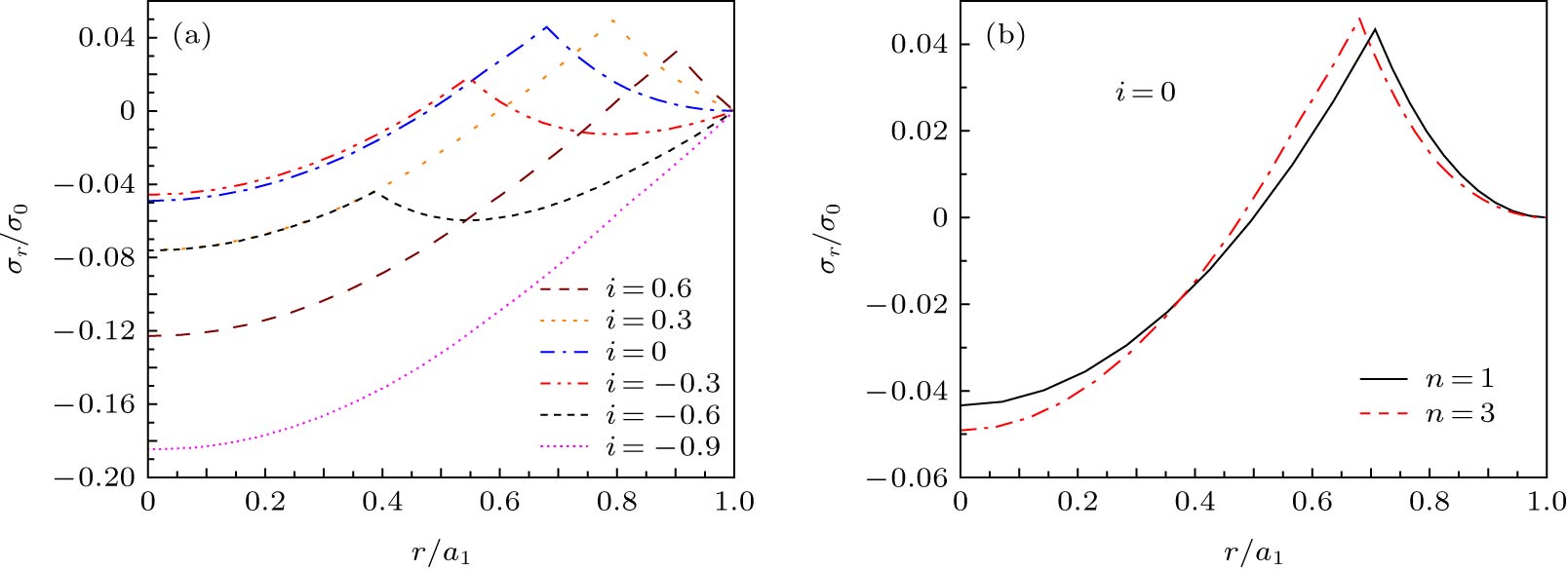
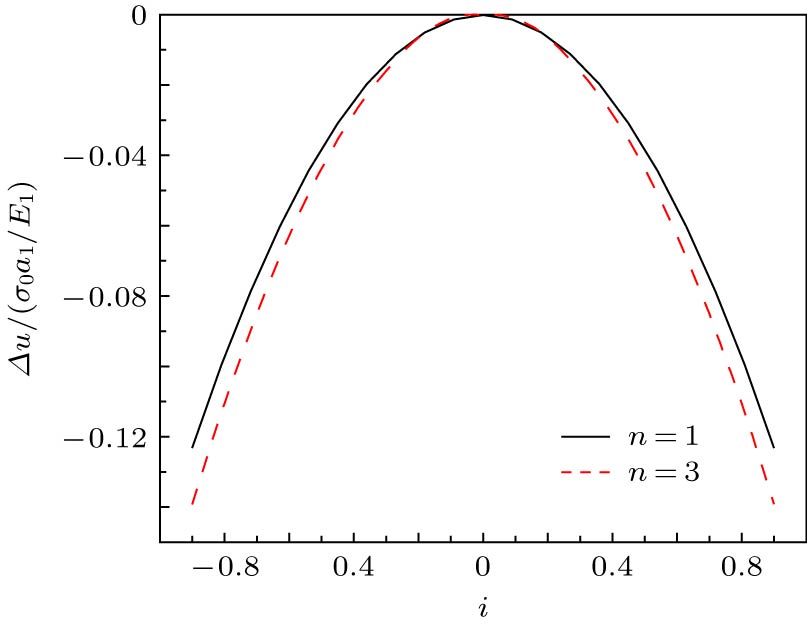
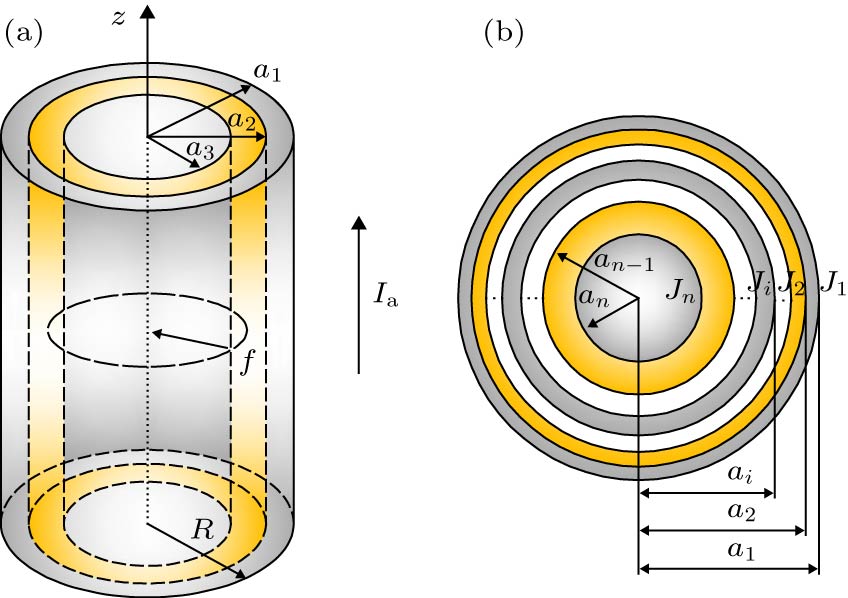
-
高温超导体具有较高的临界温度、高载流能力和低能耗特性, 在电力领域得到了广泛的应用, 其在通有承载电流情况下的力学特性得到了广泛的关注. 研究了承载电流情形下圆柱状超导结构内的磁通钉扎力学响应. 考虑临界电流密度沿径向非均匀分布, 基于临界态Bean模型, 获得了圆柱状超导结构内的感应磁场及电流的分布规律. 结合平面应变方法, 给出了结构内磁通钉扎力、应力及磁致伸缩的解析表达式. 结果表明: 临界电流密度非均匀分布时, 超导结构内的应力变化趋势与均匀分布时一致, 然而临界电流密度的非均匀分布将导致超导结构内的应力和磁致伸缩的极值增大, 并引起结构内局部径向应力大小发生改变以及环向应力分布不连续. 本研究表明临界电流密度非均匀性对超导结构力学性能的影响是显著的, 可为超导体的设计和实际应用提供参考依据.High-temperature superconductor has high critical temperature, high transport current capacity and low energy consumption, which correspondingly offer the wide applications in the field of electric power. As an important concern, the mechanical properties of superconductor carried with transport current have received extensive attention. Still, its mechanical properties in various electromagnetic environments are under study. Most of previous studies are based on the assumption of uniform distribution of critical current density, and only few researches based on the non-uniform distribution of critical current density are carried out. In this work, the mechanical flux pinning response of cylindrical superconducting structures is studied. Considering the non-uniform features of critical current density along the radial direction, the distribution law of induced magnetic field and current for the cylindrical superconducting structure is obtained based on the Bean model. Combined with the plane strain method, the analytical expression of magnetic flux pinning force, stress and magnetostriction in the superconducting structure are obtained. The results show that the uneven distribution of critical current density causes the flux pinning force to change, which further leads the superconductor`s local radial stress to vary with the critical current density. When the transport current flowing through the superconductor is increased in the ascending field, the radial stress and the hoop stress both appear compressive. The non-uniform distribution of critical current density has no significant effect on the overall trend of the internal stress, but displays an obvious influence on the stress distribution, and the superconducting structure is compressed and deformed. The results are consistent with those in the uniform case. When the transport current decreases during field descending, the critical current starts to reverse from the outermost part, then the compressive stress and tensile stress exist simultaneously. The hoop stress has a discontinuous point at the discontinuous portion of the critical current density, thus the damage probability is higher than that of the uniform distribution. In other words, the shear strength of superconductor is required to be higher for application. Also, the degree of magnetostriction is higher when the distribution of critical current density is set to be uniform, that is, the non-uniform distribution of the critical current density causes the superconducting structure to undergo greater deformation. Therefore, in engineering applications, the structural strength of the superconducting material must be enhanced to cope with the challenge from the uneven distribution of critical current density.
-
Keywords:
- cylindrical superconducting structure /
- current carrying /
- flux pinning force /
- stress strain
[1] Shinichi M, Kengo N, Hisaki S, Taro M, Ken N, Masafumi O, Tomohisa Y, Yoshiki M, Kazufumi M, Tadakazu M, Hideki S 2017 IEEE Trans. Appl. Supercond. 27 3600804
[2] Chen X Y, Jin J X, Xin Y, Shu B, Tang C L, Zhu Y P, Sun R M 2014 IEEE Trans. Appl. Supercond. 24 3801606
[3] Patel A, Hopkins S C, Baskys A, Kalitka V, Molodyk A, Glowacki B A 2015 Supercond. Sci. Technol. 28 115007
Google Scholar
[4] Larbalestier D, Gurevich A, Feldmann D M, Polyanskii A 2001 Nature 414 386
Google Scholar
[5] Ren Y T, Weinstein R M, Liu J, Sawh R P, Foster C C 1995 Physica C 251 15
Google Scholar
[6] Guan M Z, Hu Q, Gao P F, Wang X Z, Yang T J, Wu W, Xin C J, Wu B M, Ma L Z 2016 Chin. Phys. Lett. 33 58502
Google Scholar
[7] Zeng J, Zhou Y H, Yong H D 2010 J. Appl. Phys. 108 033901
Google Scholar
[8] Huang C G, Zhou Y H 2014 J. Appl. Phys. 115 033904
Google Scholar
[9] Ikuta H, Hirota N, Nakayama Y, Kitazawa K 1993 Phys. Rev. Lett. 70 2166
Google Scholar
[10] Ikuta H, Kishio K, Kitazawa K 1994 J. Appl. Phys. 76 4776
[11] Johansen T H 1999 Phys. Rev. B 60 9690
Google Scholar
[12] Johansen T H 1999 Phys. Rev. B 59 11187
Google Scholar
[13] Johansen T H, Shantsev D V 2003 Supercond. Sci. Technol. 16 1109
Google Scholar
[14] Xue C, He A, Yong H D, Zhou Y H 2013 J. Appl. Phys. 113 023901
Google Scholar
[15] Huang C G, Yong H D, Zhou Y H 2013 Supercond. Sci. Technol. 26 105007
Google Scholar
[16] Haken B T, Eck H J N V, Kate H H J T 2000 Physica C 334 163
Google Scholar
[17] Grasso G, Hensel B, Jeremie A, Flükiger R 1995 Physica C 241 45
Google Scholar
[18] Lehtonen J R, Ahoranta M, Mikkonen R 2002 Physica C 372−376 1743
[19] Inada R, Nakamura Y, Oota A 2006 Physica C 442 139
Google Scholar
[20] Sun J, Watanabe H, Hamabe M, Yamamoto N, Kawahara T, Yamaguchi S 2013 Physica C 494 297
Google Scholar
[21] Witanachchi S, Lee S Y, Song L W, Kao Y H, Shaw D T 1990 Appl. Phys. Lett. 57 2133
Google Scholar
[22] Noji H 2011 Physica C 471 995
Google Scholar
[23] Zheng Y L, Feng W J, Liu Q F 2013 J. Supercond. Novel Magn. 26 2937
Google Scholar
-
图 1 (a)长圆柱状超导结构示意图; (b)临界电流密度分布示意图
Fig. 1. (a) Schematic diagram of a long cylindrical superconducting structure; (b) schematic diagram of critical current density distribution.
图 2 上升场情形下结构内的径向应力的分布 (a) n = 3, i取不同值; (b) i = 0.9, n取不同值
Fig. 2. Distribution of radial stress in the structure under the ascending field: (a) n = 3, i takes different values; (b) i = 0.9, n takes different values.
图 3 上升场情形下结构内的环向应力的分布 (a) n = 3, i取不同值; (b) i = 0.9, n取不同值
Fig. 3. Distribution of hoop stress in the structure under the ascending field: (a) n = 3, i takes different values; (b) i = 0.9, n takes different values.
图 4 上升场情形下结构内的径向位移沿半径方向的分布
Fig. 4. Distribution of radial displacement within the structure along the radial direction in the case of an ascending field.
图 5 下降场中结构内的径向应力沿半径方向的分布 (a) n = 3, i取不同值; (b) i = 0, n取不同值
Fig. 5. Distribution of radial stress in the structure in the falling field along the radial direction: (a) n = 3, i takes different values; (b) i = 0, n takes different values.
图 6 下降场中结构内的环向应力沿半径方向的分布 (a) n = 3, i取不同值; (b) i = 0, n取不同值
Fig. 6. Distribution of the hoop stress in the structure in the falling field along the radial direction: (a) n = 3, i takes different values; (b) i = 0, n takes different values.
图 7 下降场中结构内的径向位移沿半径方向的分布
Fig. 7. Distribution of radial displacement within the structure in the descending field along the radial direction.
图 8 临界电流密度分布不同时超导圆柱体的磁致伸缩
Fig. 8. Magnetostriction of a superconducting cylinder with different critical current density distributions.
-
[1] Shinichi M, Kengo N, Hisaki S, Taro M, Ken N, Masafumi O, Tomohisa Y, Yoshiki M, Kazufumi M, Tadakazu M, Hideki S 2017 IEEE Trans. Appl. Supercond. 27 3600804
[2] Chen X Y, Jin J X, Xin Y, Shu B, Tang C L, Zhu Y P, Sun R M 2014 IEEE Trans. Appl. Supercond. 24 3801606
[3] Patel A, Hopkins S C, Baskys A, Kalitka V, Molodyk A, Glowacki B A 2015 Supercond. Sci. Technol. 28 115007
Google Scholar
[4] Larbalestier D, Gurevich A, Feldmann D M, Polyanskii A 2001 Nature 414 386
Google Scholar
[5] Ren Y T, Weinstein R M, Liu J, Sawh R P, Foster C C 1995 Physica C 251 15
Google Scholar
[6] Guan M Z, Hu Q, Gao P F, Wang X Z, Yang T J, Wu W, Xin C J, Wu B M, Ma L Z 2016 Chin. Phys. Lett. 33 58502
Google Scholar
[7] Zeng J, Zhou Y H, Yong H D 2010 J. Appl. Phys. 108 033901
Google Scholar
[8] Huang C G, Zhou Y H 2014 J. Appl. Phys. 115 033904
Google Scholar
[9] Ikuta H, Hirota N, Nakayama Y, Kitazawa K 1993 Phys. Rev. Lett. 70 2166
Google Scholar
[10] Ikuta H, Kishio K, Kitazawa K 1994 J. Appl. Phys. 76 4776
[11] Johansen T H 1999 Phys. Rev. B 60 9690
Google Scholar
[12] Johansen T H 1999 Phys. Rev. B 59 11187
Google Scholar
[13] Johansen T H, Shantsev D V 2003 Supercond. Sci. Technol. 16 1109
Google Scholar
[14] Xue C, He A, Yong H D, Zhou Y H 2013 J. Appl. Phys. 113 023901
Google Scholar
[15] Huang C G, Yong H D, Zhou Y H 2013 Supercond. Sci. Technol. 26 105007
Google Scholar
[16] Haken B T, Eck H J N V, Kate H H J T 2000 Physica C 334 163
Google Scholar
[17] Grasso G, Hensel B, Jeremie A, Flükiger R 1995 Physica C 241 45
Google Scholar
[18] Lehtonen J R, Ahoranta M, Mikkonen R 2002 Physica C 372−376 1743
[19] Inada R, Nakamura Y, Oota A 2006 Physica C 442 139
Google Scholar
[20] Sun J, Watanabe H, Hamabe M, Yamamoto N, Kawahara T, Yamaguchi S 2013 Physica C 494 297
Google Scholar
[21] Witanachchi S, Lee S Y, Song L W, Kao Y H, Shaw D T 1990 Appl. Phys. Lett. 57 2133
Google Scholar
[22] Noji H 2011 Physica C 471 995
Google Scholar
[23] Zheng Y L, Feng W J, Liu Q F 2013 J. Supercond. Novel Magn. 26 2937
Google Scholar
下载:
计量
- 文章访问数: 8032
- PDF下载量: 43
- 被引次数: 0
