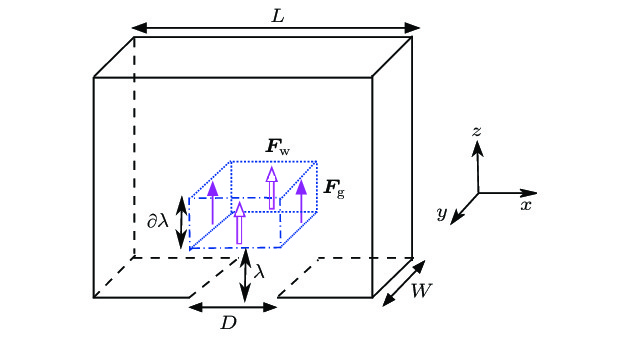
-
应用基于局部本构理论的连续数值模拟方法, 研究出口在底部和侧面的颗粒物在类三维矩形容器内的卸载现象. 重点是容器厚度W和出口高度D对颗粒物压强与速度的影响. 受力分析和数值模拟结果均表明, 距离出口较近区域的颗粒物压强与W及D呈现如下相关性: 当D/W足够小时, 压强只与D相关; 当D/W足够大时, 压强只与W相关. 且出口在底部和侧面时均有上述结果. 模拟结果还显示, 当出口在底部时, 对于模拟中所有D/W值, 出口中心处法向速度只和D相关; 当出口在侧面时, 颗粒物出口中心处法向速度则与压强变化规律一致. 由此可见, 出口处的压强并不控制颗粒物的出口法向速度. 另外, 与出口在侧面相比, 出口在底部时, 造成流量相关性规律改变的D/W临界值较大, 一般实际情况无法满足, 因此出口中心处法向速度只与D相关, 始终满足Beverloo定律.Granular medium is ubiquitous in nature, and is an important issue in many infrastructural construction projects. In particular, the gravity discharge of fine particles from a silo constitutes an important problem of research, because of its many industrial applications. However, the physical mechanism of this system remains unclear. In this work, we study the discharge of silo from the bottom or lateral orifice, by performing pseudo-three-dimensional (3D) continuum simulations based on the local constitutive theory. The simulation is two-dimensional (2D), in order to study the 3D silo, we add the lateral frictional force in the averaged momentum equation. For a rectangular silo with an orifice of height
$D$ and the silo thickness$W$ , we study the influence of the orifice size ($W$ and$D$ ) on the granular pressure and velocity. The force analysis and simulation results reveal that for the relation between the granular pressure and the orifice size, there exist two regimes: when$D/W$ is small enough, the pressure near the orifice varies only with$D$ ; when$D/W$ is large enough, the pressure varies only with$W$ . These scaling laws are the same for both bottom and lateral orifice. Somewhat surprisingly, the simulation results also show that when the orifice is at the bottom, the scaling law of the vertical velocity is different from that of the pressure; when it is on the lateral side, the scaling law of the horizontal velocity is consistent with that of the pressure. This observation contradicts a hypothesis that the flow rate of discharge is controlled by the granular pressure near the orifice, and validates the recent experimental results reported in the literature. Furthermore, the relationship between the vertical velocity and the orifice size reveals that when the orifice is at the bottom, the critical value of$D/W$ for the transition of regime is much larger than the lateral orifice case, the flow rate will depend only on$W$ when$D/W\gg50$ . This condition is hardly satisfied in practice, so the new scaling law has not yet been observed for the bottom orifice case in the literature. Furthermore, this work demonstrates that the stagnant zone has an important effect on the discharge of silo, especially for the lateral orifice case. Since a non-local constitutive law can well describe the quasi-static flow, it will be interesting to modify the local constitutive model into a non-local constitutive model, and to compare the results from the two models.-
Keywords:
- local constitutive law /
- continuum simulation /
- granular medium /
- discharge of silo
[1] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) p1
[2] 陆坤权, 刘寄星 2004 物理 33 629
Google Scholar
Lu K Q, Liu J X 2004 Physics 33 629
Google Scholar
[3] Radjai F, Dubois F 2011 Discrete-element Modeling of Granular Materials (London: Wiley-Iste) p425
[4] Midi G D R 2004 Eur. Phys. J. E 14 341
Google Scholar
[5] Jop P, Forterre Y, Pouliquen O 2006 Nature 441 727
Google Scholar
[6] Lagree P Y, Staron L, Popinet S 2011 J. Fluid Mech. 686 378
Google Scholar
[7] Staron L, Lagree P Y, Popinet S 2012 Phys. Fluids 24 103301
Google Scholar
[8] Staron L, Lagree P Y, Popinet S 2014 Eur. Phys. J. E 37 1
Google Scholar
[9] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) pp239-246
[10] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) pp87-91
[11] Sperl M 2006 Granular Matter 8 59
Google Scholar
[12] Perge C, Aguirre M A, Gago P A, Pugnaloni L A, Le Tourneau D, Géminard J C 2012 Phys. Rev. E 85 021303
Google Scholar
[13] Aguirre M A, Grande J G, Calvo A, Pugnaloni L A, Géminard J C 2011 Phys. Rev. E 83 061305
Google Scholar
[14] Beverloo W A, Leniger H A, De Velde J V 1961 J. Chem. Eng. Sci. 15 260
Google Scholar
[15] Sheldon H G, Durian D J 2010 Granular Matter 12 579
Google Scholar
[16] Thomas C C, Durian D J 2015 Phys. Rev. Lett. 114 178001
Google Scholar
[17] 张昱, 韦艳芳, 彭政, 蒋亦民, 段文山, 厚美瑛 2011 65 084502
Google Scholar
Zhang Y, Wei Y F, Peng Z, Jiang Y M, Duan W S, Hou M Y 2011 Acta Phys. Sin. 65 084502
Google Scholar
[18] Zhou Y, Lagree P Y, Popinet S, Aussillous P, Ruyer P 2017 J. Fluid Mech. 829 459
Google Scholar
[19] Lagree P Y 2007 Math. Mech. 87 486
Google Scholar
[20] Jop P, Forterre Y, Pouliquen O 2005 J. Fluid Mech. 541 167
Google Scholar
[21] Popinet S 2009 J. Comput. Phys. 228 5838
Google Scholar
[22] Janda A, Zuriguel I, Maza D 2012 Phys. Rev. Lett. 108 248001
Google Scholar
[23] Benyamine M, Djermane M, Dalloz-Dubrujeaud B, Aussillous P 2014 Phys. Rev. E 90 032201
Google Scholar
[24] Kamrin K, Koval G 2012 Phys. Rev. Lett. 108 178301
Google Scholar
-
图 2
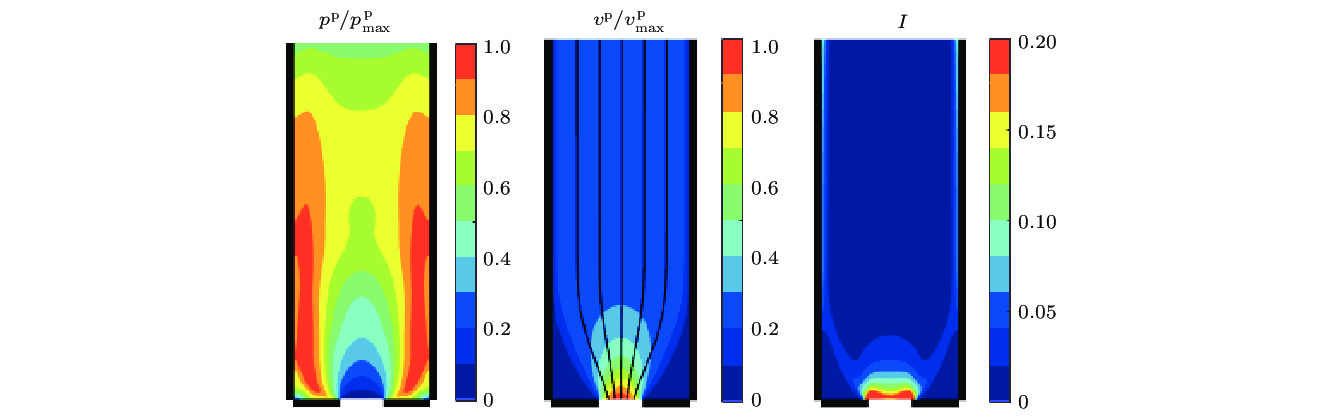
$ D = 0.3125L $ 以及$ W = 0.25L $ 情况下$ t/\sqrt{L/g} = 4 $ 时刻连续数值模拟结果, 从左至右: 容器内压强与其最大值之比; 竖直方向速度与其最大值之比, 其中黑色实线表示颗粒物流线; 无量纲常数$ I = d\sqrt{2}D_2/(\sqrt{p/\rho}) $ Fig. 2. Continuum simulation results with
$ D = 0.3125L $ and$ W = 0.25L $ at time$ t/\sqrt{L/g} = 4 $ , from the left to the right: pressure$ p^{\rm p} $ normalized by it's maximum value within the silo; the vertical velocity$ v^{\rm p} $ normalized by it's maximum value within the silo, the black lines represent the streamlines; dimensionless number$ I = d\sqrt{2}D_2/(\sqrt{p/\rho}) $ .
图 3 出口在底部情况下容器内不同区域受力图
Fig. 3. Force diagram of different zones within the silo for the case with orifice at the bottom.
图 4 在
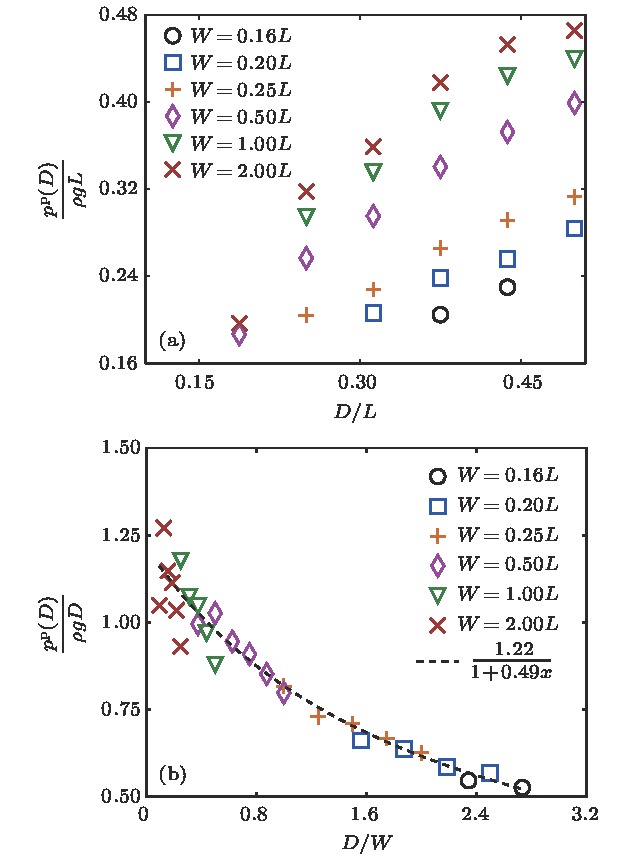
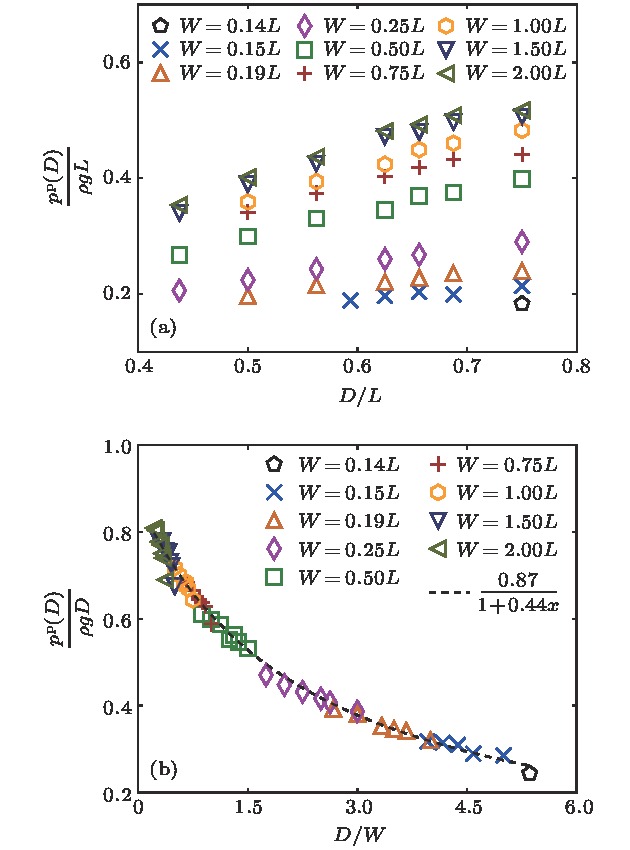
$ W $ 不同的情况下距离出口$ D $ 处的颗粒物压强$ p^{\rm p}(D) $ 结果 (a) 无量纲化压强$ p^{\rm p}(D)/(\rho g L) $ 随无量纲化出口尺寸$ D/L $ 的变化; (b) 无量纲化压强$ p^{\rm p}(D)/(\rho g D) $ 随无量纲化出口尺寸$ D/W $ 的变化Fig. 4. Results of granular pressure at the distance
$ D $ from the orifice$ p^{\rm p}(D) $ for various$ W $ : (a) Dimensionless pressure$ p^{\rm p}(D)/(\rho g L) $ vs dimensionless orifice size$ D/L $ ; (b) dimensionless pressure$ p^{\rm p}(D)/(\rho g D) $ vs dimensionless orifice size$ D/W $ .
图 5 在
$ W $ 不同的情况下位于出口处中心线的竖直方向速度$ v^{\rm p}_0 $ 结果 (a) 无量纲化速度$ {v^{\rm p}_0}^2/(2gL) $ 随无量纲化出口尺寸$ D/L $ 的变化; (b) 无量纲化速度$ {v^{\rm p}_0}^2/(2gW) $ 随无量纲化出口尺寸$ D/W $ 的变化Fig. 5. Results of vertical velocity on the central streamline
$ v^{\rm p}_0 $ for various$ W $ : (a) Dimensionless vertical velocity$ {v^{\rm p}_0}^2/(2gL) $ vs dimensionless orifice size$ D/L $ ; (b) dimensionless vertical velocity$ {v^{\rm p}_0}^2/(2gW) $ vs dimensionless orifice size$ D/W $ .
图 6
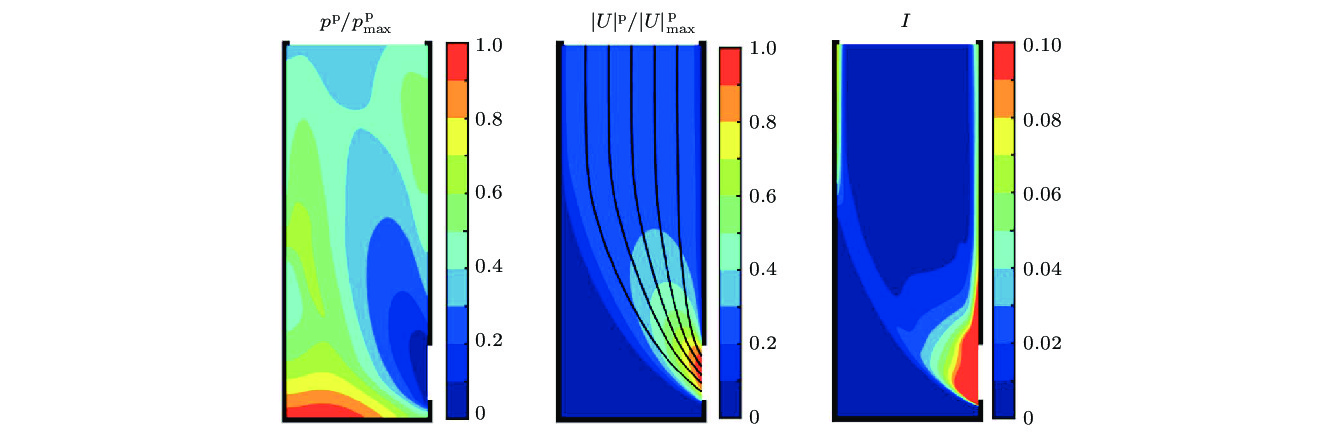
$ D = 0.40125L $ 以及$ W = 0.25L $ 情况下$ t/\sqrt{L/g} = 4 $ 时刻连续数值模拟结果, 从左至右: 容器内压强与其最大值之比; 总速度与其最大值之比, 其中黑色实线表示颗粒物流线; 无量纲常数$ I = d\sqrt{2}D_2/(\sqrt{p/\rho}) $ Fig. 6. Continuum simulation results with
$ D = 0.40125L $ and$ W = 0.25L $ at time$ t/\sqrt{L/g} = 4 $ , from the left to the right: pressure$ p^{\rm p} $ normalized by it's maximum value within the silo; the total velocity$ U^p $ normalized by it's maximum value within the silo, the black lines represent the streamlines; dimensionless number$ I = d\sqrt{2}D_2/(\sqrt{p/\rho}) $ .
图 7 出口在侧面情况下容器内不同区域受力图, 图中阴影部分代表颗粒物停滞区域
Fig. 7. Force diagram of different zones within the silo for the case with lateral orifice, the dashed area represents the stagnant zone.
图 8 在
$ W $ 不同的情况下距离出口$ D $ 处的颗粒物压强$ p^{\rm p}(D) $ 结果 (a) 无量纲化压强$ p^{\rm p}(D)/(\rho g L) $ 随无量纲化出口尺寸$ D/L $ 的变化; (b) 无量纲化压强$ p^{\rm p}(D)/(\rho g D) $ 随无量纲化出口尺寸$ D/W $ 的变化Fig. 8. Results of granular pressure at the distance
$ D $ from the orifice$ p^{\rm p}(D) $ for various$ W $ : (a) Dimensionless pressure$ p^{\rm p}(D)/(\rho g L) $ vs. dimensionless orifice size$ D/L $ ; (b) dimensionless pressure$ p^{\rm p}(D)/(\rho g D) $ vs. dimensionless orifice size$ D/W $ .
图 9 在
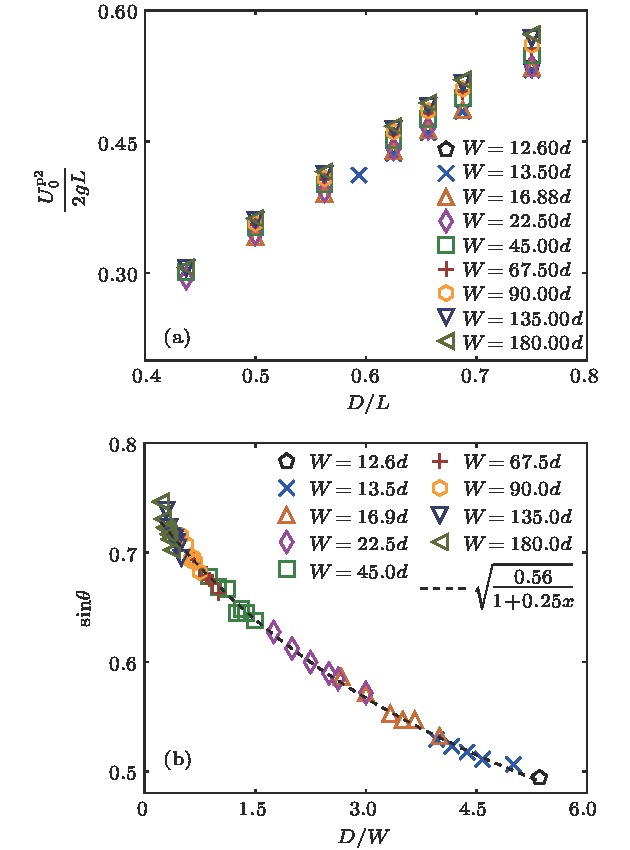
$ W $ 不同的情况下位于出口处中心流线上速度结果 (a) 无量纲化总速度$ {U_0^{\rm p}}^2/(2gL) $ 随无量纲化出口尺寸$ D/L $ 的变化; (b) 速度倾斜角$ {\rm {sin}} \theta $ 随无量纲化出口尺寸$ D/W $ 的变化Fig. 9. Results of velocity on the central streamline at the orifice for various
$ W $ : (a) Dimensionless total velocity$ {U_0^{\rm p}}^2/(2gL) $ vs dimensionless orifice size$ D/L $ ; (b) angle of inclination$ {\rm {sin}} \theta $ vs dimensionless orifice size$ D/W $ .表 1 容器及颗粒物的尺寸
Table 1. Size of silo and particle.
$h_p$ 4L $D$ [0.3125, 0.40125, 0.4375, 0.5, 0.5938,
0.625, 0.6562, 0.6875, 0.75]L$W$ [0.16, 0.2, 0.25, 0.5, 1, 2]L $d$ $L/90$ 
下载: 导出CSV
-
[1] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) p1
[2] 陆坤权, 刘寄星 2004 物理 33 629
Google Scholar
Lu K Q, Liu J X 2004 Physics 33 629
Google Scholar
[3] Radjai F, Dubois F 2011 Discrete-element Modeling of Granular Materials (London: Wiley-Iste) p425
[4] Midi G D R 2004 Eur. Phys. J. E 14 341
Google Scholar
[5] Jop P, Forterre Y, Pouliquen O 2006 Nature 441 727
Google Scholar
[6] Lagree P Y, Staron L, Popinet S 2011 J. Fluid Mech. 686 378
Google Scholar
[7] Staron L, Lagree P Y, Popinet S 2012 Phys. Fluids 24 103301
Google Scholar
[8] Staron L, Lagree P Y, Popinet S 2014 Eur. Phys. J. E 37 1
Google Scholar
[9] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) pp239-246
[10] Andreotti B, Forterre Y, Pouliquen O 2013 Granular Media: Between Fluid and Solid (Cambridge: Cambridge University Press) pp87-91
[11] Sperl M 2006 Granular Matter 8 59
Google Scholar
[12] Perge C, Aguirre M A, Gago P A, Pugnaloni L A, Le Tourneau D, Géminard J C 2012 Phys. Rev. E 85 021303
Google Scholar
[13] Aguirre M A, Grande J G, Calvo A, Pugnaloni L A, Géminard J C 2011 Phys. Rev. E 83 061305
Google Scholar
[14] Beverloo W A, Leniger H A, De Velde J V 1961 J. Chem. Eng. Sci. 15 260
Google Scholar
[15] Sheldon H G, Durian D J 2010 Granular Matter 12 579
Google Scholar
[16] Thomas C C, Durian D J 2015 Phys. Rev. Lett. 114 178001
Google Scholar
[17] 张昱, 韦艳芳, 彭政, 蒋亦民, 段文山, 厚美瑛 2011 65 084502
Google Scholar
Zhang Y, Wei Y F, Peng Z, Jiang Y M, Duan W S, Hou M Y 2011 Acta Phys. Sin. 65 084502
Google Scholar
[18] Zhou Y, Lagree P Y, Popinet S, Aussillous P, Ruyer P 2017 J. Fluid Mech. 829 459
Google Scholar
[19] Lagree P Y 2007 Math. Mech. 87 486
Google Scholar
[20] Jop P, Forterre Y, Pouliquen O 2005 J. Fluid Mech. 541 167
Google Scholar
[21] Popinet S 2009 J. Comput. Phys. 228 5838
Google Scholar
[22] Janda A, Zuriguel I, Maza D 2012 Phys. Rev. Lett. 108 248001
Google Scholar
[23] Benyamine M, Djermane M, Dalloz-Dubrujeaud B, Aussillous P 2014 Phys. Rev. E 90 032201
Google Scholar
[24] Kamrin K, Koval G 2012 Phys. Rev. Lett. 108 178301
Google Scholar
下载:
计量
- 文章访问数: 7199
- PDF下载量: 50
- 被引次数: 0
