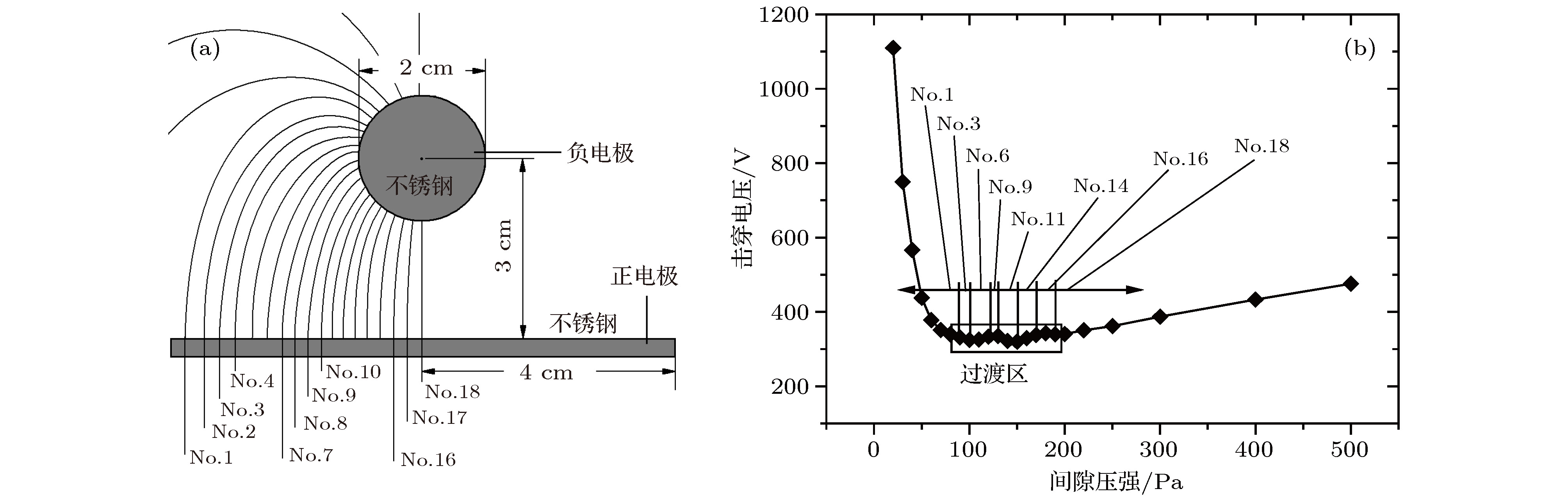
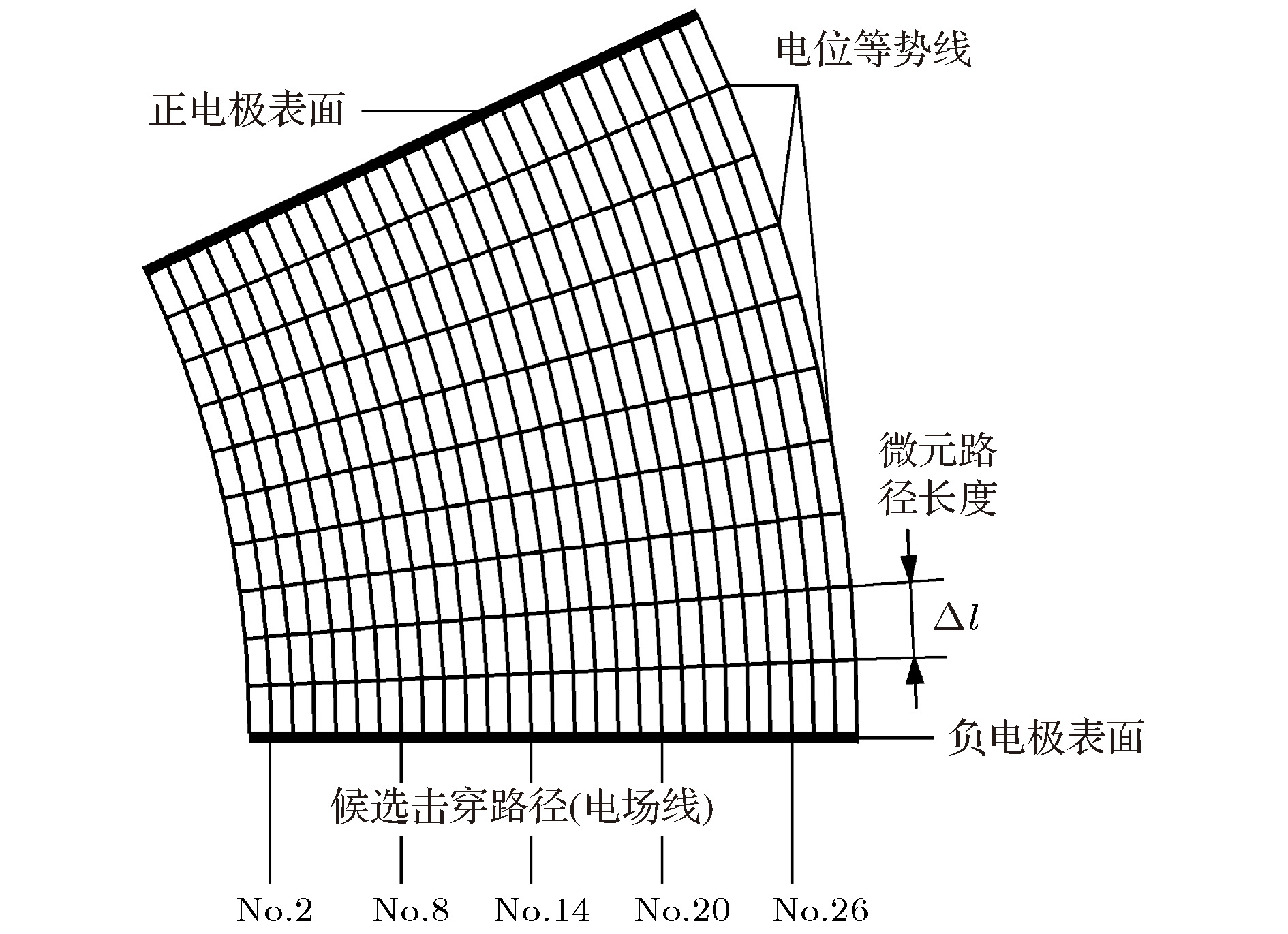
-
稍不均匀电场间隙的起始击穿路径问题对于气体放电触发以及电极表面削蚀有重要意义. 为研究低气压击穿工况中起始路径的位置规律, 本文建立了一种基于蒙特卡罗碰撞模型与电子运动轨迹假设相结合的路径判断模型(determination of the critical path 模型, DCP模型), 并以2种电极装置的击穿试验来验证DCP模型的正确性. 通过负电极表面的痕迹捕捉和击穿电压的测量可以分别验证DCP模型对起始击穿路径和击穿电压的计算能力. 根据试验结果, 起始击穿路径在不同压强或流率下会发生转移, 且转移趋势与计算结果相符; 同时, DCP模型对击穿电压的计算误差不超过7.9%, 可初步验证DCP模型的计算精度. 在此基础上, 利用DCP模型对其他4种典型的电极装置进行数值计算, 发现全部击穿案例都存在一些共性: 随着间隙压强或流率的升高, 最小电压区域((pd) min过渡区)的起始路径转移频繁, 并伴随击穿电压上下波动, 近似持平, 且起始路径几乎都服从较长路径向较短路径的转移规律. 最后, 通过DCP模型的数值分析, 揭示了上述起始路径相关规律的内在机理.The determination of the critical breakdown path in slightly uneven electric field has played a significant role in gas discharge starting process and electrode surface erosion. In order to study the law of the critical path position in the low-pressure breakdown case, a new algorithm based on the Monte-Carlo collision model and the postulation of " forward-back trajectory for electrons” is established, namely the determination of the critical path(DCP) model. In the DCP model, some electric field lines among the electrodes are regarded as the potential breakdown paths, and the probability of the excitation and ionization collisions between the electrons and the neutrals can be obtained by the Monte-Carlo model. The most probable path to trigger the breakdown will be selected from among all the potential paths, namely the critical breakdown path, and the corresponding breakdown voltage of the critical path will be calculated. A breakdown test with two different electrode devices is performed to examine the accuracy of the DCP model: the critical path and breakdown voltage obtained by the DCP could be examined respectively by capturing the surface traces of negative electrode and measuring the breakdown voltage. According to the test results, the critical breakdown path can transit at different gap pressures or flow rates, and this observation is qualitatively consistent with the calculation results. Meanwhile, the relative error maximum of the breakdown voltage obtained by DCP is less than 7.9%. The accuracy of the DCP model partly depends on the background pressure, and the background pressure in the application case should be less than 103 Pa. Based on the DCP model, the numerical analyses of another four electrode devices are conducted to acquire the common law about the critical breakdown path. According to the calculation results, the transition zone has both a high frequency of critical path transition and a " fluctuant and similarly straight” breakdown voltage curve with the gap pressure or flow rate increasing, and the critical path transition direction follows the rule of " from longer paths to shorter paths”. Lastly, the inherent laws of those regulations about the critical path are revealed by the DCP model.
-
Keywords:
- gap of slightly uneven electric field /
- critical breakdown path /
- path transition /
- numerical simulation
[1] Paschen F 1889 Wied. Annal. Phys. Chem. 37 69
[2] Golden D E, Fisher L H 1965 Phys. Rev. 139 1452
Google Scholar
[3] Kagan Y M 1991 J. Phys. D: Appl. Phys. 24 882
Google Scholar
[4] Osmokrovic P, Loncar B, Gajic-Kvascev M 2004 IEEE Trans. Plasma Sci. 32 1849
Google Scholar
[5] Osmokrovic P, Vasic A 2005 IEEE Trans. Plasma Sci. 33 1672
Google Scholar
[6] Niemeyer L, Pietronero L, Wiesmann H J 1984 Phys. Rev. Lett. 52 1033
Google Scholar
[7] Wiesmann H J, Zeller H R 1986 J. Phys. D: Appl. Phys. 60 1770
Google Scholar
[8] Niemeyer L 1987 J. Phys. D: Appl. Phys. 20 897
Google Scholar
[9] Noskov M D, Kukhta V R, Lopatin V V 1995 J. Phys. D: Appl. Phys. 28 1187
Google Scholar
[10] Dulan A, Upul S A, Marcus B B, Vernon C 2015 J. Electrostat. 73 33
Google Scholar
[11] 火元莲, 张广庶, 吕世华, 袁萍 2013 62 059201
Google Scholar
Huo Y L, Zhang G S, Lü S H, Yuan P 2013 Acta Phy. Sin. 62 059201
Google Scholar
[12] 郑殿春, 丁宁, 沈湘东, 赵大伟, 郑秋平, 魏红庆 2016 65 024703
Google Scholar
Zheng D C, Ding N, Shen X D, Zhao D W, Zheng Q P, Wei H Q 2016 Acta Phy. Sin. 65 024703
Google Scholar
[13] Townsend J S 1925 J. Franklin Inst. 200 563
Google Scholar
[14] Mahalingam S, Nieter C, Loverich J, Smithe D, Stoltz P 2009 Open Plasma Phys. J. 2 63
Google Scholar
[15] Venkattraman A, Alexeenko A A 2012 P. Plasmas 19 123515
Google Scholar
[16] Shklyaev V A, Belomyttsev S Y, Ryzhov V V 2012 J. Appl. Phys. 112 113303
Google Scholar
[17] Macheret S O, Shneider M N 2013 Phys. Plasmas 20 101608
Google Scholar
[18] Szabo J J, Warner N, Martinez-Sanchez M 2014 J. Propul. Power 30 197
Google Scholar
[19] 谢爱根, 张健, 刘斌, 王铁邦 2012 强激光与粒子束 24 481
Xie A G, Zhang J, Liu B, Wang T B 2012 High Power Laser and Particle Beams 24 481
[20] Huerta M, Ludeking L 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, USA, January 4-7, 2010 p1
[21] 武占成, 张希军, 胡有志 2012 气体放电 (北京: 国防工业出版社) 第69页
Wu Z C, Zhang X J, Hu Y Z 2012 Gas Discharge (Beijing: National Defense Industry Press) p69 (in Chinese)
[22] Daykin-Iliopoulos A, Gabriel S, Golosnoy I, Kubota K, Funaki I 2015 34th International Electric Propulsion Conference Hyogo-Kobe, Japan, July 4-10, 2015 p1
[23] Zhao Y , Qing A , Meng Y , Song Z, Lin C 2018 Scientific Reports 8 1729
[24] Zhao Y, Huang C, Qing A, Luo X 2017 IEEE Photonics Journal 9 1
-
图 1 典型非平行电极间的计算节点划分示意图
Fig. 1. Schematic diagram of the mesh grid generation in nonparallel two-electrode gap
图 2 间隙压强不均布时的
${N_{\rm{n}}}$ 计算方法Fig. 2. Computational method of the
${N_{\rm{n}}}$ in the gap of non-uniform pressure distribution
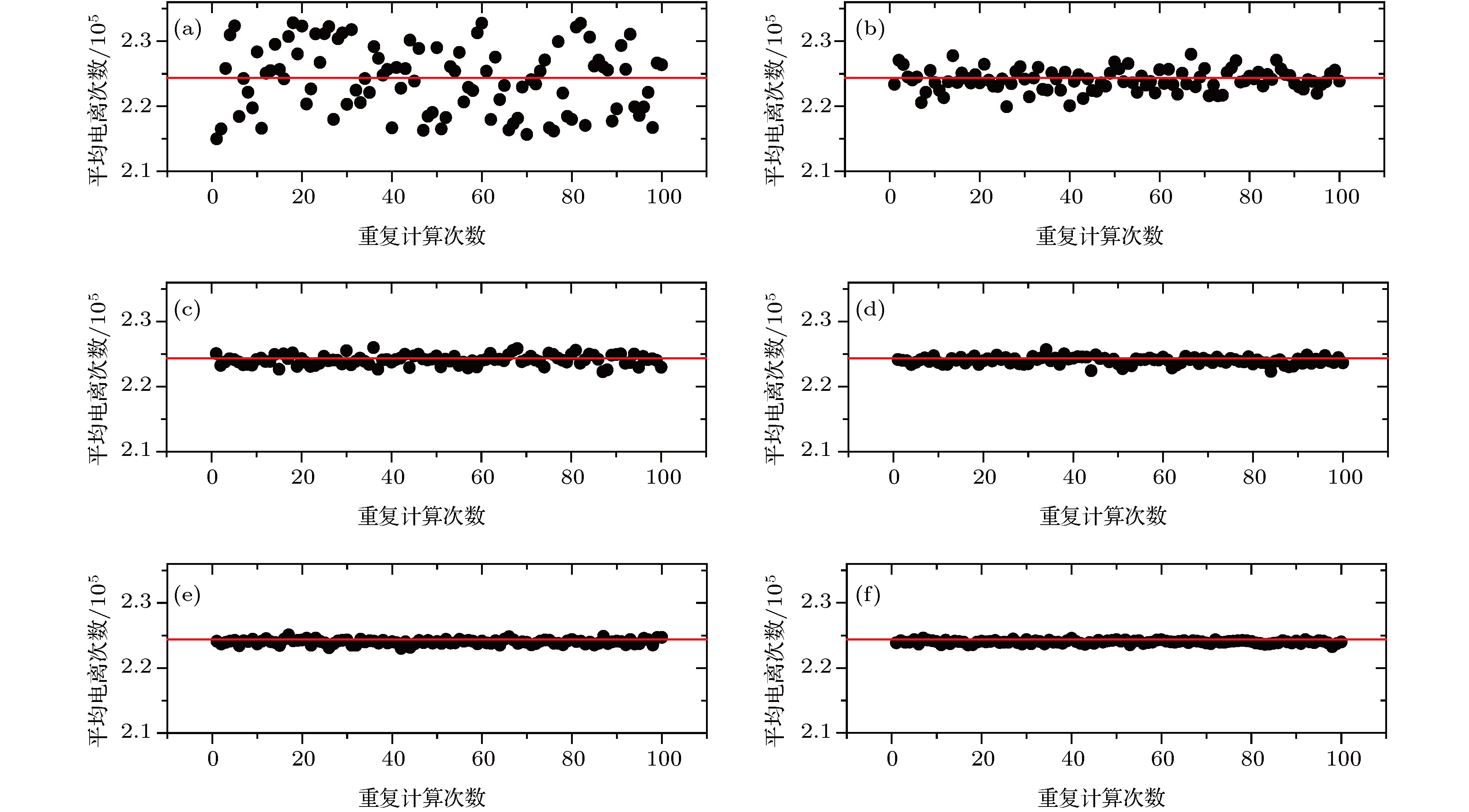
图 3 DCP计算结果稳定性随N0的依变关系(a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (case 1, 间隙压强60 Pa, 临界击穿电压345 V)
Fig. 3. The computational stability of DCP model as a function of N0: (a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (An example of case 1, gap pressure: 60 Pa, critical breakdown voltage: 345 V )
图 4 路径总电离次数的计算值随
$\Delta U$ 变化的偏差 (a) No.1候选路径; (b) No.21候选路径Fig. 4. The computational deviation of total ionization number in one path at different
$\Delta U$ : (a) Potential path of No.1; (b) potential path of No.21
图 7 圆片阶梯电极的结构及候选路径划分(f = 3.97)
Fig. 7. The geometry and potential path generation in the laddered plate electrode (f = 3.97)
图 8 Case 1试验与计算结果对比(气体工质: Xe)
Fig. 8. The comparison of the calculation and test results in case 1 (working medium: Xe)
图 9 MPDT电极的相关信息 (a)实物照片; (b)电极结构及候选路径划分(f = 2.47)
Fig. 9. The relevant information of the MPDT: (a) Physical photograph; (b) the electrode geometry and potential path generation
图 10 Case 2试验与计算结果对比(气体工质: Ar)
Fig. 10. The comparison of the calculation and test results in case 2 (working medium: Ar)
图 11 Case 3的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.45); (b)V-p曲线的计算结果及起始路径分布
Fig. 11. The input conditions and calculation results in case 3 (working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
图 12 Case 4的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 3.76); (b)V-fr曲线的计算结果及起始路径分布
Fig. 12. The input conditions and calculation results in case 4(working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
图 13 Case 5的计算输入条件及计算结果(气体工质: Ar): (a) 电极结构及候选路径划分(f = 3.43); (b) V-p曲线的计算结果及起始路径分布
Fig. 13. The input conditions and calculation results in case 5 (working medium: Ar): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
图 14 Case 6的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.84); (b)V-p曲线的计算结果及起始路径分布
Fig. 14. The input conditions and calculation results in case 6(working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
图 15 整个电极的V-p曲线形成原因(case 3)
Fig. 15. The formation reason of the entire V-p curve in the whole gap of case 3
图 16 不同压强下电极间隙的电离碰撞次数分布(case 3) (a) p = 40 Pa; (b) p = 80 Pa
Fig. 16. The ionization collision number distribution at different gap pressures in case 3: (a) p = 40 Pa; (b) p = 80 Pa
图 17
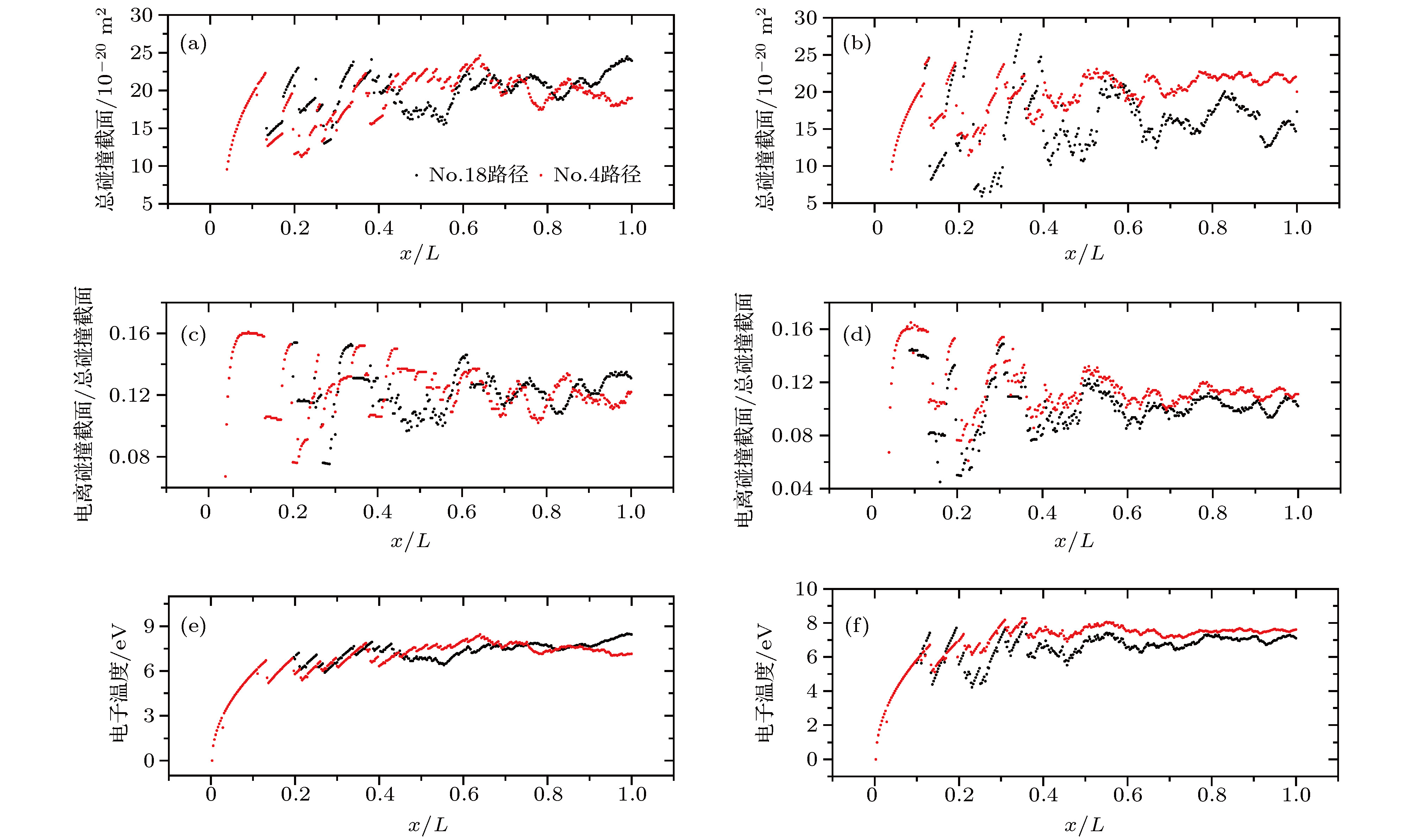
${\sigma _T}\left({E_{{k},e}}\right)$ ,${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ 和${E_{{k},e}}$ 在不同压强、不同候选路径上的分布规律(case 3) (a)平均${\sigma _T}\left({E_{{k},e}}\right)$ , p = 40 Pa; (b)平均${\sigma _T}\left({E_{{k},e}}\right)$ , p = 80 Pa; (c)平均${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ , p = 40 Pa; (d)平均${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ , p = 80 Pa; (e)平均${E_{{k},e}}$ , p = 40 Pa; (f)各节点的平均${E_{{k},e}}$ , p = 80 PaFig. 17. The distribution of
${\sigma _T}\left({E_{{k},e}}\right)$ ,${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ and${E_{{k},e}}$ at different gap pressures and different potential paths in case 3: (a) The average${\sigma _T}\left({E_{{k},e}}\right)$ , p = 40 Pa; (b) the average${\sigma _T}\left({E_{{k},e}}\right)$ , p = 80 Pa; (c) the average${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ , p = 40 Pa; (d) the average${\sigma _{{\rm{ion}}}}\left({E_{{k},e}}\right)/{\sigma _T}\left({E_{{k},e}}\right)$ , p = 80 Pa; (e) the average${E_{{k},e}}$ , p = 40 Pa; (f) the average${E_{{k},e}}$ , p = 80 Pa
图 18 不同压强下电极间隙的激发碰撞次数分布(case 3) (a) p = 40 Pa; b) p = 80 Pa
Fig. 18. The excitation collision number distribution at different gap pressures in case 3: (a) p = 40 Pa; (b) p = 80 Pa
碰撞类型 碰撞截面公式/m2 弹性碰撞 $1.699 \times {10^{ - 19}}$ ${E_{k,e}} \leqslant 0.159\; {\rm{ eV}}$ $(0.076E_{k,e}^2 - 0.345E_{k,e}^{1.5} + 0.585{E_{k,e}} - 0.427E_{k,e}^{0.5} + 0.114)\times {10^{ - 17}}$ $0.16\; {\rm{ eV}} < {E_{k,e}} \leqslant 2.8\; {\rm{ eV}}$ $( - 0.002E_{k,e}^2 + 0.03E_{k,e}^{1.5} - 0.166{E_{k,e}} + 0.402E_{k,e}^{0.5} - 0.317)\times {10^{ - 17}}$ $2.8\; {\rm{ eV}} < {E_{k,e}} \leqslant 24.7\; {\rm{ eV}}$ $( - 0.0022E_{k,e}^{1.5} + 0.043{E_{k,e}} - 0.28567E_{k,e}^{0.5} + 0.6518)\times {10^{ - 17}}$ $24.7\; {\rm{ eV}} < {E_{k,e}} \leqslant 50\; {\rm{ eV}}$ $0.00064 \times {10^{ - 17}}$ ${E_{k,e}} > 50\; {\rm{ eV}}$ 激发碰撞 $0.0$ ${E_{k,e}} \leqslant 8.4\; {\rm{ eV}}$ $(0.002E_{k,e}^2 - 0.023E_{k,e}^{1.5} + 0.098{E_{k,e}} - 0.188E_{k,e}^{0.5} + 0.135)\times {10^{ - 16}}$ $8.4\; {\rm{ eV}} < {E_{k,e}} \leqslant 11\; {\rm{ eV}}$ $(0.0007E_{k,e}^2 - 0.012E_{k,e}^{1.5} + 0.08{E_{k,e}} - 0.23E_{k,e}^{0.5} + 0.23)\times {10^{ - 17}}$ $11\; {\rm{ eV}} < {E_{k,e}} \leqslant 25\; {\rm{ eV}}$ $\begin{gathered}(0.1 \times {10^{ - 6}}E_{k,e}^2 + 0.8 \times {10^{ - 5}}E_{k,e}^{1.5} - 0.0002{E_{k,e}} + 0.002E_{k,e}^{0.5} + 0.001)\hfill \\ \times {10^{ - 17}} \hfill \\ \end{gathered} $ $25\; {\rm{ eV}} < {E_{k,e}} \leqslant 500\; {\rm{ eV}}$ 电离碰撞 $0.0$ ${E_{k,e}} \leqslant 12.1\; {\rm{ eV}}$ $(0.00136E_{k,e}^2 - 0.0226E_{k,e}^{1.5} + 0.14{E_{k,e}} - 0.38E_{k,e}^{0.5} + 0.387)\times {10^{ - 17}}$ $12.1\; {\rm{ eV}} < {E_{k,e}} \leqslant 20\; {\rm{ eV}}$ $( - 0.0006E_{k,e}^2 + 0.014E_{k,e}^{1.5} - 0.133{E_{k,e}} + 0.574E_{k,e}^{0.5} - 0.93)\times {10^{ - 17}}$ $20\; {\rm{ eV}} < {E_{k,e}} \leqslant 44\; {\rm{ eV}}$ $( - 1.6 \times {10^{ - 6}}E_{k,e}^2 + 0.1E_{k,e}^{1.5} - 0.024{E_{k,e}} + 0.022E_{k,e}^{0.5} - 0.02)\times {10^{ - 17}}$ $44\; {\rm{ eV}} < {E_{k,e}} \leqslant 360\; {\rm{ eV}}$ 
下载: 导出CSV
-
[1] Paschen F 1889 Wied. Annal. Phys. Chem. 37 69
[2] Golden D E, Fisher L H 1965 Phys. Rev. 139 1452
Google Scholar
[3] Kagan Y M 1991 J. Phys. D: Appl. Phys. 24 882
Google Scholar
[4] Osmokrovic P, Loncar B, Gajic-Kvascev M 2004 IEEE Trans. Plasma Sci. 32 1849
Google Scholar
[5] Osmokrovic P, Vasic A 2005 IEEE Trans. Plasma Sci. 33 1672
Google Scholar
[6] Niemeyer L, Pietronero L, Wiesmann H J 1984 Phys. Rev. Lett. 52 1033
Google Scholar
[7] Wiesmann H J, Zeller H R 1986 J. Phys. D: Appl. Phys. 60 1770
Google Scholar
[8] Niemeyer L 1987 J. Phys. D: Appl. Phys. 20 897
Google Scholar
[9] Noskov M D, Kukhta V R, Lopatin V V 1995 J. Phys. D: Appl. Phys. 28 1187
Google Scholar
[10] Dulan A, Upul S A, Marcus B B, Vernon C 2015 J. Electrostat. 73 33
Google Scholar
[11] 火元莲, 张广庶, 吕世华, 袁萍 2013 62 059201
Google Scholar
Huo Y L, Zhang G S, Lü S H, Yuan P 2013 Acta Phy. Sin. 62 059201
Google Scholar
[12] 郑殿春, 丁宁, 沈湘东, 赵大伟, 郑秋平, 魏红庆 2016 65 024703
Google Scholar
Zheng D C, Ding N, Shen X D, Zhao D W, Zheng Q P, Wei H Q 2016 Acta Phy. Sin. 65 024703
Google Scholar
[13] Townsend J S 1925 J. Franklin Inst. 200 563
Google Scholar
[14] Mahalingam S, Nieter C, Loverich J, Smithe D, Stoltz P 2009 Open Plasma Phys. J. 2 63
Google Scholar
[15] Venkattraman A, Alexeenko A A 2012 P. Plasmas 19 123515
Google Scholar
[16] Shklyaev V A, Belomyttsev S Y, Ryzhov V V 2012 J. Appl. Phys. 112 113303
Google Scholar
[17] Macheret S O, Shneider M N 2013 Phys. Plasmas 20 101608
Google Scholar
[18] Szabo J J, Warner N, Martinez-Sanchez M 2014 J. Propul. Power 30 197
Google Scholar
[19] 谢爱根, 张健, 刘斌, 王铁邦 2012 强激光与粒子束 24 481
Xie A G, Zhang J, Liu B, Wang T B 2012 High Power Laser and Particle Beams 24 481
[20] Huerta M, Ludeking L 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, USA, January 4-7, 2010 p1
[21] 武占成, 张希军, 胡有志 2012 气体放电 (北京: 国防工业出版社) 第69页
Wu Z C, Zhang X J, Hu Y Z 2012 Gas Discharge (Beijing: National Defense Industry Press) p69 (in Chinese)
[22] Daykin-Iliopoulos A, Gabriel S, Golosnoy I, Kubota K, Funaki I 2015 34th International Electric Propulsion Conference Hyogo-Kobe, Japan, July 4-10, 2015 p1
[23] Zhao Y , Qing A , Meng Y , Song Z, Lin C 2018 Scientific Reports 8 1729
[24] Zhao Y, Huang C, Qing A, Luo X 2017 IEEE Photonics Journal 9 1
下载:
计量
- 文章访问数: 8296
- PDF下载量: 78
- 被引次数: 0
